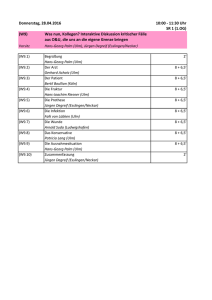
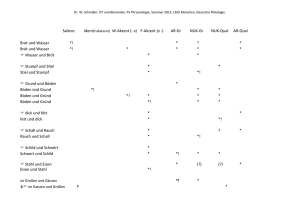
Relativistischer Energiesatz - Institut für Experimentelle Physik

ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Grundlagen der Physik 1
Mechanik und spezielle Relativität
13. 01. 2006
Othmar Marti
[email protected]
Experimentelle Physik
Universität Ulm
(c) Ulm University – p. 1/21
DO
CENDO
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Relativistische Beschleunigung
DO
CENDO
Die von B gemessene longitudinale
′
Beschleunigung a ist grösser als die
von A gemessene Beschleunigung
2 3/2
v
′
a=a 1− 2
c
(c) Ulm University – p. 2/21
·
ITÄT
U
M
Bewegte Masse
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Gedankenexperiment zur Bestimmung der
relativistischen Masse
c ist maximale Geschwindigkeit
Alle Inertialsysteme sind äquivalent
Lage des Schwerpunktes muss konsistent beschrieben
werden ⇒ m = m(v)
(c) Ulm University – p. 3/21
DO
CENDO
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Masse und Geschwindigkeit
DO
CENDO
Die mit der Geschwindigkeit v bewegte
Masse (in ihrem Ruhesystem mit m0,
Ruhemasse) hat den Wert
m0
m(v) = p
1 − v 2/c2
(c) Ulm University – p. 4/21
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Masse und Geschwindigkeit
DO
CENDO
Nach der relativistischen Mechanik
entspricht einer (geschwindigkeitsabhängigen) Masse die Energie
2
E = m(v)c
.
(c) Ulm University – p. 5/21
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Relativistische kinetische Energie
DO
CENDO
Die relativistische kinetische Energie ist
2
1
2
Ekin, rel = E−m0c = m0c
p
1 − v 2/c2
!
−1
(c) Ulm University – p. 6/21
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Relativistischer Impuls
DO
CENDO
Der relativistische Impuls ist analog zum klassischen Impuls
definiert:
m0 v
p = m(v)v = q
v2
1 − c2
(c) Ulm University – p. 7/21
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Relativistische Kraft
DO
CENDO
Die relativistische Kraft ist analog zum 2. Newtonschen
Gesetz durch
dp d (m(v)v)
=
F =
dt
dt
gegeben.
(c) Ulm University – p. 8/21
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Relativistischer Energiesatz
DO
CENDO
Relativistischer Energiesatz
q
E = m20c4 + c2p2
(c) Ulm University – p. 9/21
·
ITÄT
Relativistische Energie und
Beschleunigung
U
M
·
C
UR
· SCIENDO
DO
CENDO
Relativistische Beschleunigung
Relativistische Beschleunigung
3
1
2.5
0.8
v
2
1.5
a
ANDO · U
N
ERS
L
IV
0.6
0.4
1
0.2
0.5
0
0
0
0.5
1
1.5
t
2
2.5
3
0
0.5
1
1.5
2
2.5
3
t
Zeitverlauf der relativistischen Geschwindigkeit (links)
und der relativistischen Beschleunigung bei konstanter
Kraft.
(c) Ulm University – p. 10/21
·
ITÄT
U
M
Relativistische Energie
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
DO
CENDO
Relativistische Energie
4.5
4
3.5
Ekin
3
2.5
2
1.5
1
0.5
0
0
0.5
1
1.5
2
2.5
3
t
Verlauf der kinetischen Energie bei konstanter Kraft im
klassischen (rot) und relativistischen (grün) Fall.
(c) Ulm University – p. 11/21
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Relativistische Position
DO
CENDO
Relativistische Position
4.5
4
3.5
3
x
2.5
2
1.5
1
0.5
0
0
0.5
1
1.5
2
2.5
3
t
Verlauf der zurückgelegten Distanz bei konstanter Kraft
im klassischen (rot) und relativistischen (grün) Fall.
(c) Ulm University – p. 12/21
·
ITÄT
U
M
·
Relativistische Zeit
Relativistische Zeit
3
2.5
2
τ
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
1.5
1
0.5
0
0
0.5
1
1.5
2
2.5
3
t
Verlauf der Eigenzeit bei konstanter Kraft im
klassischen (rot) und relativistischen (grün) Fall.
(c) Ulm University – p. 13/21
DO
CENDO
·
ITÄT
U
M
Weg und Eigenzeit
·
Weg und Eigenzeit
1e+012
1e+010
1e+008
1e+006
10000
x(τ)
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
100
1
0.01
0.0001
1e-006
1e-008
0
5
10
15
20
25
τ
Zurückgelegte Strecke als Funktion der Eigenzeit.
(c) Ulm University – p. 14/21
DO
CENDO
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Lorentz-Transformation
Beschreibung eines Punktereignisses in zwei
gegeneinander bewegten Bezugssystemen
(c) Ulm University – p. 15/21
DO
CENDO
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Alternative Konstruktion zur
Lorentz-Transformation
Andere Berechnung der Lorentztransformation
(c) Ulm University – p. 16/21
DO
CENDO
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Lorentz-Transformation
DO
CENDO
Lorentz-Transformation
x − ut
x = q
u2
1 − c2
′
′
y = y
′
z = z
ux
t
−
′
c2
t = q
u2
1 − c2
′
′
x − ut
x = q
u2
1 − c2
y = y′
z = z′
ux′
′
t − c2
t = q
u2
1 − c2
(c) Ulm University – p. 17/21
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
DO
CENDO
Grösse
Ortskoordinaten
Zeitkoordinaten
Länge
Lorentz-Transformation und
Galilei-Transformation
Galilei-Transformation
klassische Physik
x; y; z
Lorentz-Transformation
relativistische Physik
x; y; z
t
ict
x = x + vt
′
′
x = √x +vt2
′
1−v /c2
vx′ /c2 +t′
t= √ 2 2
1−v /c
p
p
Abstand
r = x2 + y 2 + z 2
r = x2 + y 2 + z 2 − c2 t2
Vergleich von Galilei- und Lorentz-Transformation
Zeit
t = t′
′
(c) Ulm University – p. 18/21
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Zwillingsparadoxon
Weltlinie beim Zwillingsparadoxon
(c) Ulm University – p. 19/21
DO
CENDO
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Zwillingsparadoxon
DO
CENDO
Zwillingsparadoxon: Fahrplan der Signale, die A und B
austauschen
(c) Ulm University – p. 19/21
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Starrer Körper
DO
CENDO
Definition: ein Körper ist starr, wenn rij für beliebige i′ s
und j ′ s jederzeit konstant ist.
(c) Ulm University – p. 20/21
·
ITÄT
U
M
Starrer Körper
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Schwerpunktsystem
(c) Ulm University – p. 20/21
DO
CENDO
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Starrer Körper
DO
CENDO
Koordinatensystem zur Berechnung der Rotation eines
starren Körpers
(c) Ulm University – p. 20/21
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Starrer Körper
Definition der Eulerschen Winkel
(c) Ulm University – p. 20/21
DO
CENDO
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Kräfte am starren Körper
Angriffspunkt einer Kraft in einem starren Körper.
(c) Ulm University – p. 21/21
DO
CENDO
·
ITÄT
U
M
·
C
UR
· SCIENDO
ANDO · U
N
ERS
L
IV
Kräfte am starren Körper
Definition eines Kräftepaares.
(c) Ulm University – p. 21/21
DO
CENDO
·