Spannung - Stromstärke

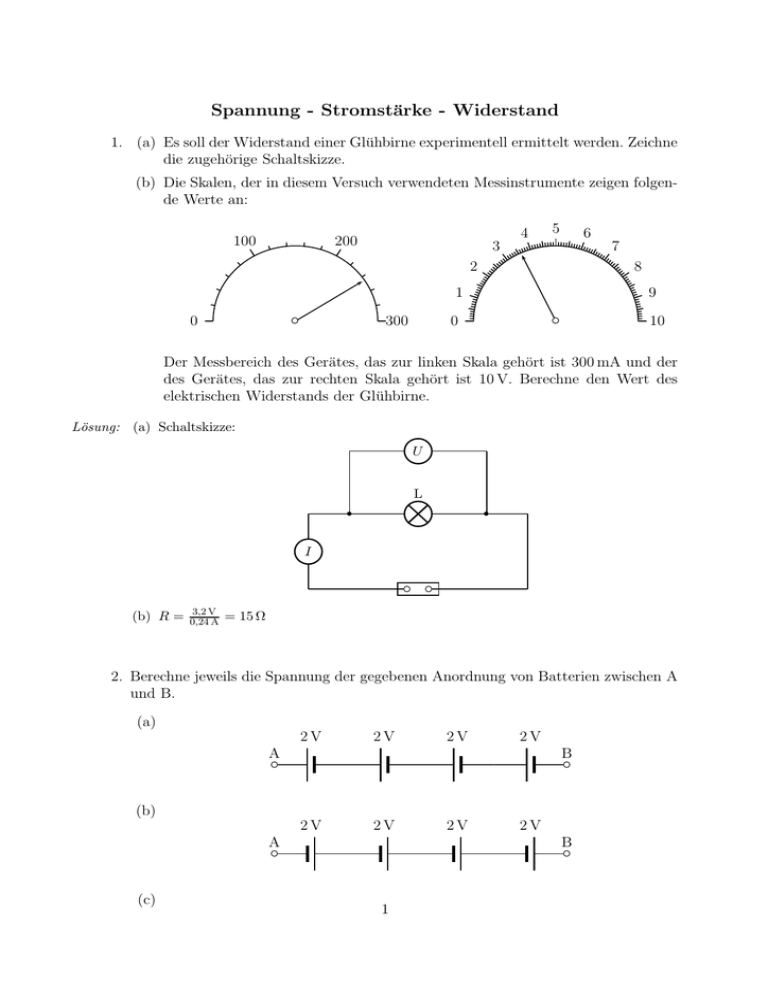
Spannung - Stromstärke - Widerstand
1. (a) Es soll der Widerstand einer Glühbirne experimentell ermittelt werden. Zeichne
die zugehörige Schaltskizze.
(b) Die Skalen, der in diesem Versuch verwendeten Messinstrumente zeigen folgende Werte an:
100
200
3
4
5
6
2
8
1
0
300
bC
7
9
0
10
bC
Der Messbereich des Gerätes, das zur linken Skala gehört ist 300 mA und der
des Gerätes, das zur rechten Skala gehört ist 10 V. Berechne den Wert des
elektrischen Widerstands der Glühbirne.
Lösung: (a) Schaltskizze:
U
L
b
b
I
bC
(b) R =
3,2 V
0,24 A
bC
= 15 Ω
2. Berechne jeweils die Spannung der gegebenen Anordnung von Batterien zwischen A
und B.
(a)
2V
2V
2V
2V
AbC
BbC
(b)
2V
2V
AbC
(c)
2V
2V
BbC
1
2V
2V
2V
2V
AbC
BbC
(d)
2V
2V
AbC
2V
2V
BbC
Lösung: 8 V; −8 V; 0; 4 V.
3. Inge hat eine ganze Schachtel voll mit 10 Ω-Widerständen. Wie kann sie daraus mit
möglichst wenig Materialverbrauch einen 8 Ω-Widerstand zusammenbauen?
Dokumentiere alle deine Versuche mit Schaltplan und Berechnung des Gesamtwiderstandes!
2
Lösung: Mögliche Lösungen:
1
1
5
1
1
=
+
=
=
(a)
R
40 Ω 10 Ω
40 Ω
8Ω
R = 8Ω
1
1
1
5
1
1
+
+
=
=
(b) ′ =
R
20 Ω 10 Ω 10 Ω
20 Ω
4Ω
′
′
R = R + R = 8Ω
1
1
1
1
5
1
(c)
=
+
+
=
=
R
40 Ω 40 Ω 40 Ω
40 Ω
8Ω
R = 8Ω
1
1
10
1
1
(d)
+3·
=
=
=
R1
30 Ω
10 Ω
30 Ω
3Ω
10 Ω
= 5 Ω, R = R1 + R2 = 8 Ω
R2 =
2
1
1
5
1
1
=
+
=
=
(e)
R1
15 Ω 10 Ω
30 Ω
6Ω
10 Ω
R2 =
= 2 Ω, R = R1 + R2 = 8 Ω
5
1
1
1
1
1
(f)
=
+
+
=
R1
30 Ω 30 Ω 10 Ω
6Ω
10 Ω
= 2 Ω, R = R1 + R2 = 8 Ω
R2 =
5
10 Ω 10 Ω 10 Ω
(g) R =
+
+
= 8Ω
2
5
10
10 Ω
(h) R = 4 ·
= 8Ω
5
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
4. In den USA hat die Netzspannung den Wert US = 115 V. Sam bringt fünf Glühlampen aus den USA mit nach Deutschland und möchte sie ans europäische Stromnetz (UE = 230 V) anschließen. Die baugleichen Lampen tragen die Aufschrift
115 V/125 W.
3
(a) Berechne den Widerstand RL einer Lampe.
(b) Sam probiert es mit nebenstehender Schaltung. Berechne den Gesamtwiderstand Rges
und den Gesamtstrom I. Welche Spannungen
U1 und U2 zeigen die beiden Messgeräte an?
U2
U1
(c) Welche Lampen sind überlastet? Eine der
überlasteten Lampen brennt durch. Erkläre
genau (mit Rechnungen), was dann mit den
anderen Lampen geschieht.
I
UE
(d) Suche eine Schaltung aller fünf Lampen, bei der mindestens eine Lampe an der
Sollspannung US liegt und die anderen Lampen nicht überlastet sind. Dokumentiere deine Versuche mit den dazugehörenden Rechnungen.
US2
U2
1152 V2
=⇒ RL = S =
= 105,8 Ω ≈ 106 Ω
RL
P
125 W
5
UE
RL RL
+
= RL = 88,2 Ω, I =
= 2,61 A
=
2
3
6
Rges
Lösung: (a) P = US IS =
(b) Rges
RL
RL
· I = 138 V, U2 =
· I = 92,0 V
2
3
(c) Die linken Lampen (U1 ) sind überlastet.
U1 =
RL
4
UE
= RL = 141 Ω, I =
= 1,63 A
3
3
RL
RL
RL
· I = 172,5 V, U2 =
· I = 57,5 V
U1 =
2
3
=⇒ Die linke Lampe brennt sofort durch und dann
brennt keine Lampe mehr.
(d) 1. Möglichkeit:
UE
U1 =
= 76,7 V,
3
UE
U2 =
= 115 V
2
2. Möglichkeit:
RL + R L
R1 =
= RL
2
UE
= 115 V
U1 = U2 =
2
An den vier linken Lampen liegt jeweils die Spannung
U1
= 57,5 V.
2
R2
U2
U1
Rges = RL +
R1
I
UE
U1
U1
U1
UE
U2
I
U2
UE
RL
U1
U2
R1
I
UE
5. (a) Welchen Widerstand R hat eine Glühlampe, die an der Spannung U = 220 V
von einem Strom der Stärke I = 0,11 A durchflossen wird?
(b) Die Bundesbahn fährt mit der Spannung U = 15 000 V. Der Widerstand des
Motors einer Lok beträgt R = 35 Ω. Welcher Strom I fließt durch den Motor?
4
(c) Welche Spannung U liegt an dem Widerstand R = 48 kΩ, der von einem Strom
der Stärke I = 25 µA durchflossen wird?
(d) Der Motor einer starken Bohrmaschine hat den Widerstand R = 18 Ω. Welche
Stromstärke muss die Sicherung mindestens aushalten?
(e) Der menschliche Körper hat, je nach Hautfeuchtigkeit, einen Widerstand von
2,5 kΩ bis 10 kΩ. Stromstärken ab ungefähr 10 mA können für den Menschen
schon lebensgefährdend sein. Ab welcher Spannung muss man also aufpassen?
U
220 V
=
= 2,0 kΩ
I
0,11 A
15 0000 V
U
=
= 4,3 · 102 A
(b) I =
R
35 V
A
Lösung: (a) R =
(c) U = RI = 48 · 103 Ω · 25 · 10−6 A = 1,2 V
U
230 V
(d) I =
=
= 13 A
V
R
18 A
(e) U = RI = 2,5 · 103 Ω · 10 · 10−3 A = 25 V
6. Die Widerstände R1 und R2 liegen hintereinander an der Spannung U, mit U1 bzw.
U2 werden die Teilspannungen an R1 bzw. R2 bezeichnet. Berechne die fehlenden
Größen:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Lösung:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
R1 in Ω
80
150
?
1000
?
50
?
R1 in Ω
80
150
9 · 105
1000
1000
50
?
R2 in Ω
120
10
30
?
?
?
80
R2 in Ω
120
10
30
?
4000
−6
80
R in Ω
?
?
?
?
5000
?
?
R in Ω
200
160
9 · 105
?
5000
44
?
U1 in V
?
5
?
0,001
?
?
?
U1 in V
4
5
299,99
0,001
100
?
?
U2 in V
6
0,33
0,01
1,999
400
?
6,4
zu (f): nicht möglich, da R2 < 0
U2
= 0,08 A 6= 0,8 A
zu (g): nicht möglich, da I =
R2
5
U2 in V
?
?
0,01
?
400
?
6,4
U in V
10
5,33
300
2
500
220
?
U in V
10
?
300
2
?
220
?
I in A
?
?
?
?
0,1
5
0,8
I in A
0,05
0,033
3,3 · 10−4
1 · 10−6
0,1
5
0,8
7. Von fünf in Reihe geschalteten Widerständen ist jeder um 100 Ω größer als sein
Vorgänger. Wie groß sind diese Widerstände, wenn bei einer angelegten Spannung
von U = 230 V ein Strom der Stärke I = 0,20 A fließt? Berechne auch die Teilspannungen an den einzelnen Widerständen.
Lösung: R + R + 100 Ω + R + 200 Ω + R + 300 Ω + R + 400 Ω =
5R + 1000 Ω = 1150 Ω
=⇒
U
= 1150 Ω
I
R = 30 Ω
U1 = 30 Ω · I = 6 V, U2 = 26 V, U2 = 46 V, U2 = 66 V, U2 = 86 V
Probe: U1 + U2 + U3 + U4 + U5 = U
8. Berechne den Ersatzwiderstand der nachstehend abgebildeten Schaltung.
R3 = 5,0 Ω
R2 = 10 Ω
R4 = 5,0 Ω
bC
b
b
b
b
R1 = 30 Ω
R5 = 5,0 Ω
R6 = 5,0 Ω
Lösung: R1 , R2 parallel: R12 = 7,5 Ω
R5 , R6 in Reihe: R56 = 10 Ω
R3 , R4 , R56 parallel: R3456 = 2,5 Ω
R12 , R3456 in Reihe: R123456 = 10 Ω
9. (a) Berechne den Ersatzwiderstand
R1 zwischen A und B.
A
B
bC
R
bC
b
R
6
R
b
bC
(b) Berechne den Ersatzwiderstand
R2 zwischen A und B unter Verwendung des Ergebnisses der vorhergehenden Teilaufgabe.
A
B
bC
R
bC
R
b
R
b
R
b
R
b
R
(c) Die ersten beiden Schaltungen kann man als Elemente einer Folge von Schaltungen auffassen. Zeichne das nächste Element dieser Folge und berechne den
Widerstand R3 dieser Schaltung.
(d) Wir legen R0 = R fest. Wie lautet dann die Formel zur Berechnung von Rn+1
aus R und Rn (n ∈ N)?
1 · R · R0
3
= R
1 · R + R0
2
13
2 · R · R1
R
=
(b) R2 =
2 · R + R1
7
A
(c)
Lösung: (a) R1 =
B
bC
R
R
bC
R
R
b
b
R
R
b
R
b
R
b
R
b
R
R3 =
(d) Rn+1
73
3 · R · R2
=
R
3 · R + R2
34
(n + 1) · R · Rn
=
(n + 1) · R + Rn
7
10. Die Batterie eines liegen gebliebenen
Pkws ist entladen und hat eine Quellenspannung von 11 V. Die Batterie mit der
der liegen gebliebene Pkw gestartet werden soll, ist voll aufgeladen und hat eine
Klemmenspannung von 12 V. Der Innenwiderstand einer Batterie beträgt jeweils
0,020 Ω und der Widerstand je eines Starthilfekabels 0,0050 Ω. Die nebenstehende
Schaltskizze gibt die Situation für gegeneinander geschaltete Batterien wieder. Berechne den Strom beim Fremdstarten für
0,0050 Ω
0,020 Ω
12 V
0,020 Ω
0,0050 Ω
11 V
(a) gegeneinandergeschaltete Batterien,
(b) gleichgeschaltete Batterien.
12 V − 11 V
= 20,0 A
0,020 Ω + 0,010 Ω + 0,020 Ω
12 V + 11 V
(b)
= 460 A
0,020 Ω + 0,010 Ω + 0,020 Ω
Lösung: (a)
11. Berechne den Gesamtwiderstand RAB der nebenstehend gezeichneten Schaltung!
3,0 Ω
1,25 Ω
1,0 Ω
B
A
4,0 Ω
2,0 Ω
Lösung: Parallelschaltung aus 3,0 Ω und 1,0 Ω ergibt R1 = 0,75 Ω.
Reihenschaltung aus 1,25 Ω und R1 ergibt 2,0 Ω.
Parallelschaltung aus 2,0 Ω und 6,0 Ω ergibt Rges = 1,5 Ω.
In der nebenstehenden Schaltung sind
zwei Widerstände R1 und R2 parallel geschaltet. Durch den Widerstand
R1 fließt ein Strom der Stärke I1 und
durch den Widerstand R2 ein Strom
12. der Stärke I2 . Nun wird ein dritter Widerstand R3 zu R1 bzw. R2 parallel
geschaltet. Welche Aussage kann man
dann über die Gesamtstromstärke Ig
und die Teilstromstärken I1 , I2 machen
(Begründung)?
8
Ig
b
b
I1
I2
R3
R1
b
R2
b
Lösung: Bei der Parallelschaltung von R3 zu R1 bzw. R2 sinkt der Gesamtwiderstand der Schaltung, also nimmt die Gesamtstromstärke zu. In jedem Teilstromkreis ist aber die Spannung
gleich der Klemmenspannung der Batterie, d. h. dass I1 und I2 sich nicht verändern.
13. Du hast ein Glühlämpchen mit der Aufschrift 4,5 V / 1,35 W, zwei 10 Ω-Widerstände
und eine 12 V-Autobatterie. Finde eine Schaltung aus den gegebenen Bauteilen, mit
der das Lämpchen ohne Schaden zu nehmen betrieben werden kann. Dokumentiere
alle deine Versuche mit Schaltplan und Berechnung der Lampenspannung UL .
Lösung: Sollstrom durch die Lampe: I0 =
1,35 VA
= 0,30 A
4,5V
RL
10 Ω
4,5V
= 15 Ω
Lampenwiderstand: RL =
0,3 A
U
10 · 15 Ω
= 16 Ω, I =
= 0,75 A
Rges = 10 Ω +
10 + 15
Rges
UL
I
10 Ω
UL = 0,75 A · 6 Ω = 4,5 V
U
Schaltungen, die nicht zum Ziel führen:
RL
10 Ω
I1
I1
10 Ω
I2
I2
I
U
UL = 12 V
Roben = 25 Ω
U
I1 =
= 0,48 A
Roben
15
· 12 V = 7,2 V
UL =
25
U
= 0,343 A
Rges
15
· 12 V = 5,14 V
35
UL
RL
U
Rges = 35 Ω
10 Ω
10 Ω
U
UL =
UL
10 Ω
10 Ω
UL
I=
RL
U1
14. In nebenstehender Schaltung gilt
R1 = 1,0 Ω, R2 = 1,0 Ω, R3 = 2,0 Ω und
R4 = 5,0 Ω. Durch R1 fließt der Strom
I1 , durch R2 der Strom I2 usw.
R2
R1
R3
A
B
R4
(a) Berechne den Gesamtwiderstand RAB zwischen den Punkten A und B.
(b) Wie groß ist die Spannung UAB zwischen den Punkten A und B, wenn durch
R2 der Strom I2 = 3,0 A fließt?
Lösung: (a) R2k3 =
RAB =
2
1 · 2Ω
= Ω,
1+2
3
R123 · R4
=
R123 + R4
R123 = R1 + R2k3 =
5
3
· 5Ω
20
3
=
25
Ω = 1,25 Ω
20
9
5
Ω
3
(b) U2 = R2 I2 = 3 V,
U1 = R1 I1 = 4,5 V,
U2
= 1,5 A,
I1 = I2 + I3 = 4,5 A
R3
UAB = U1 + U2 = 7,5 V
I3 =
15. Für eine Standard–LED ist die zulässige Betriebsspannung 2,1 V. Dabei fließt durch
die LED ein Strom der Stärke 10 mA. Welchen Vorwiderstand muss man wählen,
wenn für den Betrieb der LED nur eine Batterie mit einer Klemmenspannung von
9,0 V zur Verfügung steht?
Lösung:
9,0 V − 2,1 V
= 0,69 kΩ
10 mA
10