Vorlesung 14

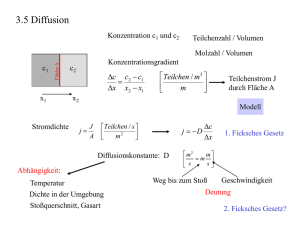
Einführung in die Physik I
Wärmelehre/Thermodynamik
Wintersemester 2007
Vladimir Dyakonov
#14 am 31.01.2007
Folien im PDF Format unter:
http://www.physik.uni-wuerzburg.de/EP6/teaching.html
Raum E143, Tel. 888-5875, eMail: [email protected]
Antwort des Tages
Man mischt 1 kg schmelzendes Eis und 1 kg siedendes
Wasser:
1 kg H2O,
T=100°C
1 kg Eis, T=0°C
T=?
T=10°C
T=50°C
T=75°C
1
Frage des Tages
Man mischt 1 kg schmelzendes Eis und 1 kg siedendes
Wasser:
∆λ=335 kJ/kg
C (H2O)=4.18 kJ/kg K
1kg Eis + 1kg H20
∆Q=m C ∆T
Lösung:
∆Q (in 1kg Wasser @ ∆T=100°C) =418 kJ
∆Q (Rest nach dem Schmelzen)=418kJ - 335 kJ= 80 kJ
∆T=80kJ / (2kg x 4.18kJ/kg K)= 10°C
10.11 Wärmetransport
T1
T2
Bringt man zwei Wärmebäder mit unterschiedlicher
Temperatur in engen Kontakt, so stellt sich nach
einer gewissen Zeit ein thermisches Gleichgewicht
ein
Das ursprünglich wärmere Reservoir wird kälter und
das ursprünglich kältere wird wärmer
Tm
2
10.11 Wärmetransport
10.11 Wärmetransport
Konvektion
Konvektion (von lat. convehere = mittragen, mitnehmen),
auch Thermische Konvektion, ist der Transport von Stoffen
oder physikalischen Eigenschaften durch die Bewegung von
Teilchen.
Ein Mechanismus zum Transport von thermischer Energie.
Konvektion ist dadurch gekennzeichnet, dass die
Wärmeübertragung durch den Transport von Teilchen, die ihre
kinetische Energie mitführen, bewerkstelligt wird.
3
10.11 Wärmetransport
Konvektion
• Verbunden mit Materietransport
• Ursache: Temperaturabhängigkeit der
Dichte
• In Festkörpern ohne Bedeutung
Der Mechanismus:
• Erwärmung von unten oder innen
• Abkühlung von oben
• Thermische Ausdehnung -> Auftrieb
• Heißes Material steigt auf
• kühlt an Oberfläche ab
• sinkt als kaltes Material ab
10.11 Marangoni-Konvektion
• Durch Verdunsten der Flüssigkeit auf der Oberfläche bildet sich ein
Temperaturgradient aus, der eine Konvektion in der Flüssigkeitsschicht erzeugt.
• An den Stellen, an denen die Flüssigkeit absteigt, sammelt sich das Pulver am Boden
der Petrischale und erzeugt Strukturen.
Alternativ:
• Durch eine wellenförmige Störung bilden sich Wellentäler und Wellenberge aus. Da die
Wellentäler näher an der Wärmequelle liegen, haben sie eine höhere Temperatur. Bei
höherer Temperatur sinkt jedoch die Oberflächenspannung.
• Der Unterschied der Oberflächenspannung zwischen den Bergen und Tälern ist die
Kraft, die eine Konvektion zwischen diesen antreibt.
4
10.11 Rayleigh-Benard-Konvektion
Bei der Wärmeausdehnung nimmt die Dichte von Gasen
/Flüssigkeiten mit steigender Temperatur ab
Kühlen
Heizen
Wärmere Bereiche steigen nach oben
10.11 Rayleigh-Benard-Konvektion
5
10.11 Wärmetransport
Wärmestrom durch Konvektion:
α
A
∆T
Wand: T
= Wärmeübergangskoeffizient
= Querschnittsfläche
= Temperaturdifferenz
∆Q / ∆t = α A(T1 - T2 ) ∝ ∆T
Fläche A
• Insgesamt schwierig zu beschreiben durch die Beteiligung vieler
Effekte:
Auftrieb, Viskosität, Wärmeleitung, Oberflächenspannung
• Konvektion kann z.B. durch poröse Materialien unterdrückt
werden (poröse Dämpfstoffe)
• Strömung transportiert die Wärme effektiver als die Wärmeleitung
10.11 Wärmetransport
Konvektion
„freie Konvektion“:
Vorgang findet selbsttätig statt
• „erzwungene Konvektion“:
Wenn z.B. durch eine Umwälzpumpe die Bewegung von Materie
erzwungen wird
• Wärmemenge, die bei der Konvektion transportiert wird, entspricht
dem Wärmeinhalt der transportierten Materie: z.B. Fernheizung
Bei der Fernheizung wird 100 °C heißer Wasserdampf durch
wärmeisolierte Rohre geschickt, kondensiert beim
Endverbraucher und kühlt sich auf ca. 40 °C ab.
Kondensationswärme: 540 cal/g
Abkühlung:
60 cal/g
6
10.11 Wärmeleitung in Festkörpern
• Kein Massentransport
• Für den Transport der Wärme ist ein Temperaturgefälle notwendig
• Wärmeleitung in festen Stoffen beruht auf Kopplung zwischen
benachbarten Atomen, so dass Schwingungsenergie von einem Atom
auf ein anderes übertragen werden kann
• Bsp.: Heizplatte & Bratpfanne
d.h. Wärme wird durch Materie, die selbst in Ruhe bleibt, fortgeleitet
10.11 Wärmeleitung in Festkörpern
7
10.11 Wärmeleitung in Festkörpern
Wärmeleitung in Festkörpern: Stationärer Zustand
Irreversibler Vorgang
Wärmemenge ∆Q lauft in der Zeit ∆t vom
wärmeren zum kälteren Bad (T1 > T2)
P=
dQ
T −T
= j ⋅ A = Aλ 1 2
dt
L
Wärmeleitungsgleichung
Die Temperaturverteilung ist linear längs x
T1 − T2
L
dT
j = −λ
dx
=
−
∆T
∆x
dQ/dt ist der Wärmestrom
10.11 Wärmeleitung in Festkörpern
Allgemeine Form der Wärmeleitungsgleichung (stationärer Fall):
r
⎛ dT dT dT ⎞
⎟⎟ .
j = −λ gradT = −λ ⎜⎜
,
,
⎝ dx dy dz ⎠
Gleichung gilt nur für den stationären Fall, wenn also das TemperaturGefälle durch geeignete Maßnahmen ständig aufrechterhalten wird.
d.h. in einem herausgegriffenen Volumenelement bleibt die Temperatur
konstant: Es fließt genauso viel Wärme zu wie ab
8
10.11 Wärmeleitung in Festkörpern
Temperaturverteilung im stationären Zustand:
T(x)
T ( x) = −
dQ / dt
x + T1
λA
T1
x
Temperaturverteilung im nicht-stationären Zustand:
∂T
λ ∂ 2T
=−
⋅
∂t
ρc ∂ 2 x 2
λ/ρc = Temperaturleitzahl
10.11 Wärmeleitung in Festkörpern
Stoff
Silber
Wärmeleitfähigkeit in W / m ·K
420
Kupfer
390
Aluminium
230
Konstantan (40% Ni, 60% Cu) 22
Quarzglas
1,4
Wasser
0.54 (keine Konvektion)
Polymere
Luft
≈ 0.15
0.024 (keine Konvektion)
9
10.11 Wärmeleitung in Festkörpern
Wärmeleitung in Festkörpern
Isolatoren:
• Wärmeleitung durch Phononen(gas)
• Phononendichte ~ Temperatur
• Phononen strömen aus Bereichen hoher Dichte → niedriger Dichte
Metalle:
• Wärmeleitung durch Leitungselektronen
• Elektronen quasifrei zwischen den Metallatomen (Elektronengas).
• hohe λ‘s in Metallen: zusätzlicher Beitrag der Leitungselektronen
Hohe elektrische Leitfähigkeit σ sind mit hohen Werten für λ verknüpft:
λ
= const ⋅ T
σ
Empirisch:
Wiedemann-Franzsches Gesetz,
(gilt nicht bei tiefen Temperaturen)
10.11 Wärmeleitung in Festkörpern
Zeitliche Entwicklung der Temperaturverteilung:
Die Wärmestrom-Bilanz aus Zu-/Abfluß in einem Volumenelement ist:
dV
j x dy dz
⎛
⎞
dj
⎜⎜ j x + x dx ⎟⎟ dy dz
dx
⎝
⎠
1 dQ ⎞
⎛
⎜j= ⋅
⎟
A dt ⎠
⎝
Insgesamt ist pro Zeiteinheit die Wärmemenge dQ abgeflossen:
10
10.11 Wärmeleitung in Festkörpern
d jy d jz
⎛ dj
dQ
= −⎜⎜ x +
+
dy
dz
dt
⎝ dx
r
⎞
⎟⎟ dx dy dz = − div j ⋅ dV .
⎠
Diese Wärmemenge erzeugt eine Temperaturerhöhung im Volumenelement.
ρ: Dichte, m: Masse,
C: Wärmekapazität
c: spez. Wärmekap.
dQ
dT
dT
dT
=C
= dm c
= ρ dV c
.
dt
dt
dt
dt
r
dT
1
=−
div j .
ρc
dt
Die Temperaturerhöhung ist
Mit:
r
j = −λ gradT
und mit
dT
λ
=
div grad T
dt
ρc
folgt:
div grad T ≡ ∆ T ,
dT
λ ⎛ d 2T d 2T d 2T
⎜
=
+
+
dt
ρ c ⎜⎝ dx 2 dy 2 dz 2
(∆: Laplace-Operator)
⎞
⎟⎟
⎠
folgt:
λ
T& =
∆T.
ρc
oder
Differentialgleichung der Wärmeleitung
10.11 Wärmeleitung in Festkörpern
Die Gesamtentropien ändert sich wie:
d S = d S1 + d S 2
T1
T2
Die Änderung der Entropie S1 ist
d S1 =
dQ
dT
=C
T
T
integrieren liefert:
Tm
1
T
∆ S1 = C ∫ dT = C ln m
T
T1
T1
Tm
ebenso:
T
∆ S 2 = C ln m
T2
Es folgt:
∆ S = ∆ S1 + ∆ S 2 = C ln
Tm2
T1 ⋅ T2
11
10.11 Wärmeleitung in Festkörpern
• Der Prozess des Temperaturausgleichs läuft von selbst ab.
• Die Entropie verrät aber nicht wie schnell er abläuft.
• Das Experiment zeigt: die Wärmemenge, die pro Zeit durch eine Fläche A fließt, ist
proportional zur Temperaturänderung senkrecht zur Fläche.
P=
dQ
dt
P=
Q
t
dQ
dt
wenn zeitlich konstant
A
r r
P = ∫ j ⋅ dA
r r
P = j ⋅A
grad T
wenn räumlich konstant
x
10.11 Wärmeleitung in Festkörpern
dT
λ
=
∆T
dt ρ c
Achtung: Delta bedeutet hier den Laplaceoperator
Die zweiten Ableitungen im Laplace-Operator glätten eine vorgegebene
Temperaturverteilung aus:
dT
>0
dt
d 2T
>0
d x2
d 2T
<0
d x2
d 2T
<0
d x2
d 2T
>0
d x2
d 2T
>0
d x2
Das System konvergiert in Richtung thermodynamisches Gleichgewicht
12