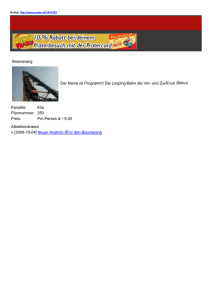
x ϕ m L y

INSTITUT FÜR MATHEMATISCHE PHYSIK
Prof. Dr. P. Recher
Dipl.-Phys. L. Weithofer
Theoretische Mechanik
3. Übungsblatt
SoSe 2012
Abgabe: Montag, 30.04.2012, zwischen Raum A305 und Raum A306 bis 14:00 Uhr
1. Schiefer Wurf am Hang
5 Punkte
Ein Stein wird mit der Anfangsgeschwindigkeit v0 unter einem Winkel θ gegen die Horizontale
y v
0
Θ
α
x
s
an einem Hang mit Neigungswinkel α abgeworfen.
(a) Bestimmen Sie die Bewegungsgleichung, die Bahnkurve und die Wurfweite s(θ).
(b) Zeigen Sie, dass die größtmögliche Wurfweite bei θ = π/4 − α/2 erzielt wird.
2. Fadenpendel
4 Punkte
Eine Punktmasse m ist an einem langen dünnen Faden der Länge L aufgehängt und führt
kleine Schwingungen um ihre Ruhelage aus.
x
y
ϕ
L
m
(a) Zeigen Sie, dass die Bewegung mit einer Differentialgleichung der Form
d2
x(t) + ω02 x(t) = 0
dt 2
beschrieben werden kann und bestimmen Sie ω0 .
(1)
Hinweise:
• Fertigen Sie eine Skizze des Problems an und zeichnen Sie die an der Punktmasse
angreifende Gewichtskraft und Zwangskraft (durch die Aufhängung) ein.
• Berechnen Sie die resultierende Kraft (d.h. die Kraftkomponente der Gewichtskraft
senkrecht zur Aufhängung) und stellen Sie die Newton’sche Bewegungsgleichung
in zwei Dimensionen auf.
• Führen Sie geeignete Näherungen für den Fall kleiner Auslenkungen durch und begründen Sie so Gleichung (1).
(b) Bestimmen Sie die Lösung der Differentialgleichung (1). Verwenden Sie als Ansatz
x(t) = e λt .
Als Anfangsbedingungen können x(t = 0) = A und ẋ(t = 0) = 0 angenommen werden.
3. Zugkraft
2 Punkte
Ein Körper der Masse M liegt reibungsfrei auf einer Ebene. Eine weitere Masse m hängt an
einem (masselosen) Faden, die reibungslos über eine Rolle mit der Masse M verbunden ist.
Ermitteln Sie die Beschleunigungen der Massen M und m und die Zugkraft auf den Faden.
M
m
4. Autofahrer
3.5 Punkte
(a) Ein Autofahrer macht bei einer Geschwindigkeit v eine Vollbremsung. Wie weit ist der
Bremsweg?
Hinweis: Die Gleitreibungskraft entspricht betragsmäßig der Normalkraft multipliziert
mit einem Gleitreibungskoeffizienten µGR , also |F GR | = µGR |F N |. Der Gleitreibungskoeffizient kann hier als gegeben angenommen werden.
(b) Ein Autofahrer fährt mit konstanter Geschwindigkeit v um die Kurve. Finden Sie den
minimalen Radius der Kurve, sodass das Auto bei gegebenem Haftreibungskoeffizienten
µHR nicht rutscht.
Hinweis: Die maximale Haftreibungskraft (d.h. die Kraft, bei der das Auto gerade nicht
rutscht) kann als |F HR | = µHR |F N | angenommen werden.
(c) Ein Autofahrer fährt direkt auf eine (unendlich breite) Mauer zu. Er kann entweder eine
Vollbremsung machen oder bei gleicher Geschwindigkeit wenden, um die Kollision zu
vermeiden. Verwenden Sie die Ergebnisse von a) und b) um zu zeigen, unter welcher
Bedingung für die Reibungskoeffizienten er bremsen sollte (Alles was zählt ist, ob die
Kollision stattfindet oder nicht).
(d) Angenommen, die Mauer sei nur 2L breit, und das Auto fährt ursprünglich direkt auf
die Mitte des Hindernisses zu. Ermitteln Sie bei gegebenen Reibungskoeffizienten den
minimalen Wert für L, bei dem der Autofahrer sich dazu entschließen sollte, zu wenden.