26.09.2016

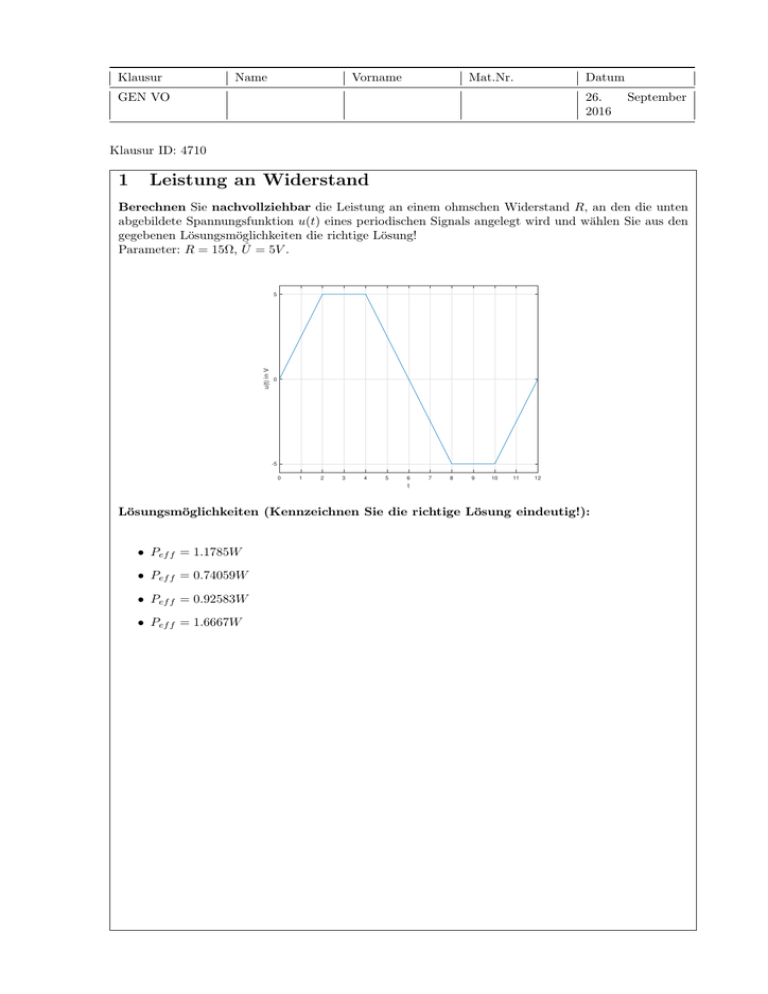
Klausur
Name
Vorname
Mat.Nr.
Datum
GEN VO
26.
2016
September
Klausur ID: 4710
1
Leistung an Widerstand
Berechnen Sie nachvollziehbar die Leistung an einem ohmschen Widerstand R, an den die unten
abgebildete Spannungsfunktion u(t) eines periodischen Signals angelegt wird und wählen Sie aus den
gegebenen Lösungsmöglichkeiten die richtige Lösung!
Parameter: R = 15Ω, Û = 5V .
u(t) in V
5
0
-5
0
1
2
3
4
5
6
7
8
9
10
11
12
t
Lösungsmöglichkeiten (Kennzeichnen Sie die richtige Lösung eindeutig!):
• Pef f = 1.1785W
• Pef f = 0.74059W
• Pef f = 0.92583W
• Pef f = 1.6667W
2
Differenzialgleichung
Gegeben ist die nachfolgend abgebildete Schaltung . Die Differenzialgleichung für den Strom iL (t) an
I0
1
1 ′
iL + LC
iL = LC
. Grundsätzlich gibt es 3 mögliche homogene Lösungen:
der Spule lautet: i′′L + RC
• iLh = e−δt [K1 cosh Ωt + K2 sinh Ωt]
• iLh = e−δt [K1 t + K2 ]
• iLh = e−δt [K1 cos Ωt + K2 sin Ωt]
Geben Sie die charakteristische Gleichung an und finden Sie heraus, welcher Fall vorliegt. Berechnen
Sie dann die Konstanten K1 und K2 . Nehmen Sie dabei an, dass Kondensator und Spule zum Zeitpunkt
t = 0s ungeladen sind.
Parameter: I0 = 3V , R = 6Ω, C = 9µF, L = 0.001296H
Hinweis: 5e − 05 bedeutet 5 ∗ 10−5 !
Lösungsmöglichkeiten (Kennzeichnen Sie die richtige Lösung eindeutig!):
• K1 : −2.8e + 04A/s; K2 : 3A
• K1 : 0.00032A/s; K2 : 3A
• K1 : 2.8e + 04A/s; K2 : −3A
• K1 : −2.8e + 04A/s; K2 : −3A
3
Spannungsteiler
Gegeben ist das unten abgebildete Netzwerk. Berechnen Sie nachvollziehbar die Ausgangsspannung
ua als Sinusfunktion (Phasenwinkel in Grad) und wählen Sie aus den nachfolgenden Lösungsmöglichkeiten die richtige aus.
Parameter: ue = 120V sin(ωt), R = 9Ω, L = 0.14H, C = 0.00012F , f = 100Hz.
Hinweis: 5e − 05 bedeutet 5 ∗ 10−5 !
Lösungsmöglichkeiten (Kennzeichnen Sie die richtige Lösung eindeutig!):
• ua = 1.27V sin(ωt + 89.40◦ )
• ua = 102.11V sin(ωt + −1.03◦ )
• ua = 67.38V sin(ωt + 55.84◦ )
• ua = 70.55V sin(ωt + 60.05◦ )
4
Quellenumwandlung
Gegeben ist die nachfolgend abgebildete Schaltung . Berechnen Sie die Spannung der Ersatzquelle U
(Zählpfeil beachten) und den resultierenden Innenwiderstand R und wählen Sie aus den nachfolgenden
Lösungsmöglichkeiten die richtige Lösung aus.
Parameter: U2 = 14V , I1 = 0.7A, R2 = 18Ω, R1 = 14.4Ω
Lösungsmöglichkeiten (Kennzeichnen Sie die richtige Lösung eindeutig!):
• U = 0.62V ; R = 3.24Ω
• U = 0.62V ; R = 8.00Ω
• U = 0.44V ; R = 13.86Ω
• U = 0.47V ; R = 8.00Ω
5
Kirchhoff ’sche Regeln
Gegeben ist der unten abgebildete Teil eines Netzwerks. Berechnen Sie die Spannung UR4 mit Hilfe
der Kirchhoff’schen Knoten- und Maschenregeln und wählen Sie die korrekte Lösung aus!
Parameter: Un1 = 4V , Un2 = 7V , Un3 = 4V , Uq = 8V , R2 = 7Ω, IR2 = 0.3A.
Lösungsmöglichkeiten (Kennzeichnen Sie die richtige Lösung eindeutig!):
• UR4 = −1.2V
• UR4 = −7V
• UR4 = −2.1V
• UR4 = −5.1V
6
Zeigerdiagramm
Gegeben ist das unten abgebildete Netzwerk. Dieses wird mit einer Wechselspannung betrieben.
Wählen Sie aus den unten abgebildeten Zeigerdiagramme das richtige aus!
Parameter: |U 0 | = 5V , R1 = 5Ω, R2 = 6Ω, L = 4mH, ω = 1000s−1 .
Hinweis: 5e − 05 bedeutet 5 ∗ 10−5 !
Lösungsmöglichkeiten (Kennzeichnen Sie die richtige Lösung eindeutig!):
0
IR2
0
U R1
-2
Im
U0
Im
-1
1
U R2
IR2
-3
-1
U0
-2
IR1
IL
-4
-3
IR1
-3
-2
-1
0
1
0
1
Re
2
Re
1
Im
0
-1
IR1
U R1
IL
U R2
U0
-2
IR2
-3
-4
-3
-2
Re
absatzdummy
IL
U R1
U R2
-1
0
3
4
7
Schwingkreis
Gegeben ist das unten abgebildete Netzwerk. Berechnen Sie die Resonanzfrequenz ω0 und wählen Sie
aus den gegebenen Lösungsmöglichkeiten die richtige Lösung aus!
Parameter: R = 50Ω, L = 0.02H, C = 3e − 06F .
Hinweis: 5e − 05 bedeutet 5 ∗ 10−5 !
Lösungsmöglichkeiten (Kennzeichnen Sie die richtige Lösung eindeutig!):
• ω0 =
q
1
CL
2
− (R
L ) = 3.2E + 03
• ω0 =
q
R
CL
−
• ω0 =
q
1
CL
R
− (C
) = 1.7E + 07
• ω0 =
q
1
CL
= 4.1E + 03
1
(RL)2
= 2.9E + 04
8
Einschaltverhalten
Das gegebene Netzwerk soll bezüglich seines Schaltverhaltens untersucht werden. Der Schalter S sei
für t < 0 in Position 2 und wird bei t = 0 in Position 1 gebracht. Wählen Sie aus den gegebenen
Kurvenverläufen den richtigen Verlauf für iL (t) und uL (t) aus und begründen Sie Ihre Wahl in
Stichworten!
(Strom: rote volle Linie; Spannung: blaue strichlierte Linie)
Parameter: U0 = 5V , R = 1000Ω, L = 0.005H, iL (t = 0) = 0.01A.
Lösungsmöglichkeiten (Kennzeichnen Sie die richtige Lösung eindeutig!):
−3
x 10
5
4
4
4
4
3
3
3
3
2
2
2
2
1
1
1
1
0
0
−1
0
1
2
t/τ
3
4
L
L
0
−1
iL(t)/[A]
5
u (t)/[V]
x 10
5
i (t)/[A]
uL(t)/[V]
−3
5
5
0
0
1
2
t/τ
3
4
5
−3
x 10
5
5
−3
x 10
10
4
4
3
3
2
2
1
−2
8
−3
7
1
−4
6
0
−5
−1
L
0
−1
0
absatzdummy
1
2
t/τ
3
4
5
iL(t)/[A]
9
uL(t)/[V]
−1
i (t)/[A]
uL(t)/[V]
0
5
0
1
2
t/τ
3
4
5