Blatt 11 - Universität Ulm

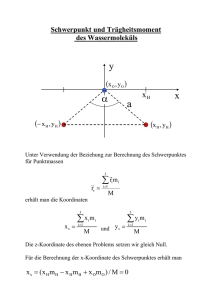
Universität Ulm
Institut für Festkörperphysik
Prof. Dr. P. Ziemann
20.01.2011
Seminar zur ‚Mechanik‘, WS 2010/11, Blatt 11 zum 27.01.
Aufgabe 51: Drehimpulssatz
Ein Experimentator sitzt auf einem Drehstuhl und hält zwei Hanteln an den ausgestreckten Armen. Er erhält einen Stoß und dreht sich mit 0,5 Umdrehungen/s. Dann
zieht er die Hanteln an seinen Körper. Wie schnell dreht er sich jetzt, wenn die ursprünglich 0,6 m von der Drehachse entfernten Hanteln auf einen Abstand von 0,1 m
herangezogen wurden? Die Masse der Hanteln sei so, dass Experimentator und
Hanteln bei 0,6 m Abstand den gleichen Drehimpuls besitzen.
Aufgabe 52: Trägheitsmoment: Seilrolle
Zwei Körper mit den Massen m1 = 100 g und m2 = 150 g sind mit einer (masselosen)
Schnur miteinander verbunden. Diese Schnur laufe über eine Rolle (homogene, dünne
Scheibe, reibungsfrei gelagert) mit der Masse M = 100 g und dem Radius R = 10 cm.
Die Schnur gleite nicht auf der Rolle.
a) Bestimmen Sie die Beschleunigungen der Körper!
b) Wie groß sind die Zugkräfte in beiden Teilen der Schnur?
c) Wie lauten die Ergebnisse, wenn das Trägheitsmoment der Rolle vernachlässigt
würde?
Aufgabe 53: Trägheitsmoment: Kippen eines Würfels
a) Berechnen Sie das Trägheitsmoment eines homogenen Würfels um eine seiner
Kanten.
b) Dieser Würfel gleite reibungsfrei über eine Platte und stoße inelastisch mit einer
ganzen Kante so an ein Hindernis, dass der Würfel zu kippen beginnt.
Bestimmen Sie die Geschwindigkeit v0 des Würfels, bei der der Würfel nicht auf
die Platte zurückkippt, sondern vornüber kippt.
Aufgabe 54: Rotierender Körper: Energiesatz
Auf eine horizontal (reibungslos) gelagerte Trommel vom Radius R und der Masse M
ist ein (masseloses) Seil gewickelt, an dem die Masse m = M/2 hängt.
a) Berechnen Sie die Winkelgeschwindigkeit ω der Trommel als Funktion der Zeit!
b) Wie groß muss der Trommelradius sein, wenn in einer Minute die Drehzahl ν =
94 s-1 erreicht werden soll?
Aufgabe 55: Trägheitstensor
Ein Quader mit den Kantenlängen a, b, c und mit den körpereigenen Koordinaten x, y,
t
z durch seinen Schwerpunkt wird durch seinen Trägheitstensor Θ charakterisiert.
a) Berechnen Sie die Komponenten des auf seine Hauptachsen transformierten
Tensors!
b) Der Quader rotiere um seine Raumdiagonale, berechnen Sie das Trägheitsmoment
ΘD!
c) Die Rotation um die Raumdiagonale sei durch zwei Lager fixiert. Berechnen Sie
die Richtung des Drehimpulses und begründen Sie das Auftreten von Drehmomenten auf die Lager.
Aufgabe 56: Kreisel
Eine homogen Scheibe mit der Masse 2 kg und dem Radius 6 cm sei auf halber Länge
einer 10 cm langen, massefreien, waagrecht positionierten Achse montiert und rotiere
mit 900 Umdrehungen in der Minute. Die Achse sei an ihrem einen Ende reibungsfrei
gelagert und werde an ihrem anderen Ende mit einer Anfangsgeschwindigkeit in horizontaler Richtung bewegt, sodass die Präzession ohne Nutation verläuft.
a) Bestimmen Sie die Winkelgeschwindigkeit der Präzession!
b) Wie groß ist die Geschwindigkeit des Schwerpunkts während der Präzession?
c) Wie groß ist die Beschleunigung des Schwerpunkt und welche Richtung hat sie?
d) Wie groß sind die horizontalen und vertikalen Komponenten der Kraft, die das
Lager ausübt?