Thermodynamik I

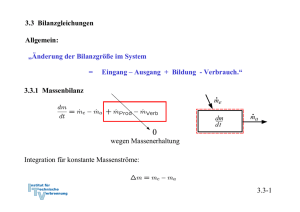
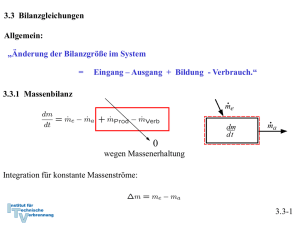
Thermodynamik I
Sommersemester 2012
Kapitel 3, Teil 2
Prof. Dr.-Ing. Heinz Pitsch
Kapitel 3, Teil 2: Übersicht
3 Energiebilanz
3.3 Bilanzgleichungen
3.3.1 Massebilanz
3.3.2 Energiebilanz und 1. Hauptsatz der Thermodynamik
3.3.3 Spezifische Wärmekapazitäten
3.3.4 Kreisprozesse und Zustandsgrößen
3.3.5 Bewertung thermodynamischer Prozesse
3.3.6 Stationärer Fließprozess
3.3.7 Energiebilanz bei Mischung feuchter Luft
2
3.3 Bilanzgleichungen
• Allgemein:
Änderung der Bilanzgröße im System
=
Eingang – Ausgang + Bildung - Verbrauch
3.3.1 Massenbilanz
wegen Massenerhaltung
0
• Integration für konstante Massenströme:
3
3.3.2 Energiebilanz und 1. Hauptsatz der Thermodynamik
0
wegen Energieerhaltung
oder
1. Hauptsatz der
Thermodynamik
Integration von 1 nach 2:
Änderung im
System
4
Flüsse:
• Arbeit
• Wärme
• Energie mit Massenstrom
Verschiedene Schreibweisen
•
Integrale Form:
•
Ratenform:
•
Massenbezogene integrale Form:
•
Massenbezogene differentielle Form:
Merke: Unterschied zwischen vollständigem Differential (d) und
infinitesimaler Menge Energie (d)
-
•
Formulierung der Energiebilanz:
1. Geschlossenes oder offenes System
2. Absolut- oder Ratenform
3. Spezifisch oder Massenform
5
Energiebilanz in geschlossenen Systemen
•
Zustandsänderung
•
Zustandsänderung 1  2
oder
bzw.
6
Beispiel 1: Wasserdampf in Zylinder
m = 5 kg
p1 = 500 kPa, J1 = 200 oC
p2 = p1 = 500 kPa, J2 = 120 oC
Fragen:
1.
Wie groß ist die ausgetauschte Wärmemenge Q12?
2.
Skizze im T,v – Diagramm!
•
Lösung
7
1. Geschlossenes oder offenes System?
 Geschlossen
2. Absolut- oder Ratenform?
 Absolut
3. Spezifisch oder Massenform?
 Massenform
Beispiel 1: Wasserdampf in Zylinder
1. Hauptsatz:
•
Es ist:
DEkin = DEpot = 0
•
[E] :
•
Arbeit bei isobarer Zustandsänderung:
•
Einsetzen
•
Für Q12 folgt
Volumenänderungsarbeit
8
Stoffdaten
Zustand 1 (500 kPa, 200oC) überhitzt
Zustand 2 (500 kPa, 120oC) unterkühlt
9
Tabelle Überhitzter Dampf
Inkompressible Flüssigkeit,
Sättigungstabelle
Skizze im T,v - Diagramm
10
Zustand 2
Näherung:
u’ (J2) = 503,5 kJ/kg, v’ (J2) = 0,00106 m3/kg
( h’(J2) = 503,71 kJ/kg )
Sättigungsenthalpie gute Näherung,
h2 (J2) = 504,03 kJ/kg
aber oft nicht genau genug!
11
Zustand 1
h1 = 2855,4 kJ/kg
Q12 = m (h2-h1) = 5 kg (504,03 kJ/kg - 2855,4 kJ/kg)  - 11757 kJ
12
Kapitel 3, Teil 2: Übersicht
3 Energiebilanz
3.3 Bilanzgleichungen
3.3.1 Massebilanz
3.3.2 Energiebilanz und 1. Hauptsatz der Thermodynamik
3.3.3 Spezifische Wärmekapazitäten
3.3.4 Kreisprozesse und Zustandsgrößen
3.3.5 Bewertung thermodynamischer Prozesse
3.3.6 Stationärer Fließprozess
3.3.7 Energiebilanz bei Mischung feuchter Luft
17
3.3.3 Spezifische Wärmekapazitäten
Spezifische Wärmekapazitäten bei konstantem Volumen: cv
•Änderung der Inneren Energie u = u(T,v):
•Definition der spezifischen Wärmekapazität bei
konstantem Volumen:
•Wir betrachten die Änderung der inneren Energie auf
Grund der Temperaturänderung für den
isochoren Prozess
•Dann gilt
18
und
Isochorer Prozess
1. Hauptsatz für isochoren Prozess
V = const
Mit
folgt
•
cv ist die spezifische Wärme, die zugeführt werden muss, um die Temperatur
für ein Kilogramm des Stoffes im System bei konstantem Volumen um 1 K zu
erhöhen
19
Spez. Wärmekapazität bei konstantem Druck: cp
•
Änderung der Enthalpie h = h(T,p)
•
Definition der spezifischen Wärmekapazität bei konstantem Druck:
•
Wir betrachten die Änderung der Enthalpie auf Grund einer
Temperaturänderung für einen isobaren Prozess
•
Dann gilt
20
und
Isobarer Prozess
1. Hauptsatz für isobaren Prozess
Mit
folgt
und
•
cp ist die spezifische Wärme, die zugeführt werden muss, um die Temperatur
für ein Kilogramm des Stoffes im System bei konstantem Druck um 1 K zu
erhöhen
21
Spezifische Wärmekapazitäten idealer Gase
• Bei idealen Gasen sind die innere Energie und die Enthalpie ausschließlich
Funktionen der Temperatur
• Daher gilt für ideale Gase immer
• Daher müssen auch die spezifischen Wärmekapazitäten idealer Gase reine
Temperaturfunktionen sein
• Mit
und damit
22
folgt durch Ableitung
Spezifische Wärmekapazitäten idealer Gase
• Verhältnis der spezifischen Wärmen: k *)
• Daraus ergibt sich
• Aus Diagramm
- Einatomige Gase:
cp/R ≈ 5/2  k ≈ 5/3 = 1,66
- Zweiatomige Gase: cp/R ≈ 7/2  k ≈ 7/5 = 1,4
Verhältnis der spezifischen Wärmen k spielt eine besondere Rolle. Wir werden sehen, dass für die idealen
Gase k gleich dem sogenannten Isentropenxponenten k ist.
*) Das
23
Spezifische Wärmekapazitäten idealer Flüssigkeiten
•
Annahme: Inkompressibel, d. h. konstantes Volumen: dv = 0
•
Aus vollständigem Differential
•
folgt, dass
, und damit dass die innere Energie eine reine
Temperaturfunktion ist
•
1. Hauptsatz liefert mit pdv = 0:
24
Folgerung für Enthalpie idealer Flüssigkeiten und cp
• Definition der Enthalpie:
• Vollständiges Differential:
• Vergleich:
 Wärmekapazitäten cp und cv sind gleich für ideale Flüssigkeiten
• Enthalpie für ideale Flüssigkeiten hängt also von Temperatur und Druck ab
• Kalorische Zustandsgleichung lautet
Integration
25
Kapitel 3, Teil 2: Übersicht
3 Energiebilanz
3.3 Bilanzgleichungen
3.3.1 Massebilanz
3.3.2 Energiebilanz und 1. Hauptsatz der Thermodynamik
3.3.3 Spezifische Wärmekapazitäten
3.3.4 Kreisprozesse und Zustandsgrößen
3.3.5 Bewertung thermodynamischer Prozesse
3.3.6 Stationärer Fließprozess
3.3.7 Energiebilanz bei Mischung feuchter Luft
26
3.3.4 Kreisprozesse und Zustandsgrößen
• Definition:
Ändert ein System Zustand so, dass es
vom Anfangszustand 1 über Zwischenzustände wieder zum Anfangszustand
zurückkehrt 2=1, hat das System einen
Kreisprozess durchlaufen
• Für jede Zustandsgröße z = f(z1,z2) gilt:
• Umgekehrt: Verschwindet das Umlaufintegral
Zustandsgröße
, so ist z eine
Darstellung von Kreisprozessen mit quasistatischen
Zustandsänderungen
rechtslaufender Kreisprozess
linkslaufender Kreisprozess
(Arbeit wird an Umgebung abgegeben)
(Arbeit wird von Umgebung zugeführt)
•Umlaufintegrale verschwinden nicht
•Volumenänderungsarbeit ist also keine Zustandsgröße sondern eine
Prozessgröße!
Zustands- und Prozessgrößen
• Zustandgrößen z besitzen ein vollständiges Differential: dz
zum Beispiel: Volumen V: dV , Druck p: dp , innere Energie U: dU
• Genauso wie Volumenänderungsarbeit ist auch die ausgetauschte Wärme keine
Zustandsgröße, sondern vom Prozessverlauf abhängig
• Wärme Q und Volumenänderungsarbeit WV besitzen kein vollständiges
Differential
 Kleine Menge Wärme, Arbeit: dQ und dWV = - p dV
• Erster Hauptsatz in differentieller Form:
• Unterscheidung zwischen Zustands- und Prozessgrößen auch in der Indizierung bei
integraler Schreibweise:
Gesamtbilanz Kreisprozess
Erster Hauptsatz
n+1 Einzelschritte:
0-1:
1-2:
2-3:
.
.
.
.
n-0:
S insgesamt:
aber:
Kapitel 3, Teil 2: Übersicht
3 Energiebilanz
3.3 Bilanzgleichungen
3.3.1 Massebilanz
3.3.2 Energiebilanz und 1. Hauptsatz der Thermodynamik
3.3.3 Spezifische Wärmekapazitäten
3.3.4 Kreisprozesse und Zustandsgrößen
3.3.5 Bewertung thermodynamischer Prozesse
3.3.6 Stationärer Fließprozess
3.3.7 Energiebilanz bei Mischung feuchter Luft
31
3.3.5 Bewertung thermodynamischer Prozesse
•
Generell: Vergleich von Nutzen zu Aufwand
•
bei Arbeitsmaschinen  thermischer Wirkungsgrad hth
•
bei Kühlprozessen und Wärmepumpen:  Leistungszahl e
32
Beispiel: Otto-Motor
• Viertaktmotor (schematisch)
33
Der idealisierte Otto-Prozess (Gleichraumprozess)
•
Ideales Gas mit konstanten Wärmekapazitäten
•
Luft als Arbeitsmedium
•
Vernachlässigung von Verlusten ↔ Annahme reversibler Prozesse
•
Massenaustausch mit Umgebung (Ein- und Ausschieben) bleibt
unberücksichtigt
 Geschlossenes System
•
Ladungswechsel durch Wärmeabfuhr ersetzt
•
Verbrennung wird durch Wärmezufuhr ersetzt
•
Kompression und Expansion werden als reversibel-adiabate Prozesse
aufgefasst
•
Wärmezufuhr und Wärmeabfuhr erfolgen bei konstantem Volumen
34
Darstellung im p,V-Diagramm
12
Adiabate & reibungsfreie Kompression
23
Isochore Wärmezufuhr: Verbrennung
34
Adiabate & reibungsfreie Expansion: Arbeit
41
Isochore Wärmeabfuhr: Ladungswechsel
Wirkungsgrad:
35
Bilanz des Kreisprozesses
• Wirkungsgrad:
• 1. HS Gesamtsystem
• Analyse
• Für adiabate und reibungsfreie
Zustandsänderungen folgt
1  2:
3  4:
Bilanz des Kreisprozesses
• Verbrennung 2  3
1. HS 2 3 :
Mit
folgt
• Wärmeabfuhr 4  1
1. HS 4 1 :
Mit
Thermischer Wirkungsgrad:
folgt
37
Thermischer Wirkungsgrad
• Thermischer Wirkungsgrad
• Bestimmung der Temperaturverhältnisse:
analog
.
.
.
38
Thermischer Wirkungsgrad: Idealisierter Otto-Prozess
• Aus
folgt mit pVk = C oder p = C/Vk
und
• Wirkungsgrad steigt mit Verdichtungsverhältnis ɛ an
.
*) Werden Wärmeverluste bei Kompression und Expansion und andere Verluste berücksichtigt, so kann
statt des Isentropenexponenten k auch ein adäquater Polytropenexponent n verwendet werden
39
Kapitel 3, Teil 2: Übersicht
3 Energiebilanz
3.3 Bilanzgleichungen
3.3.1 Massebilanz
3.3.2 Energiebilanz und 1. Hauptsatz der Thermodynamik
3.3.3 Spezifische Wärmekapazitäten
3.3.4 Kreisprozesse und Zustandsgrößen
3.3.5 Bewertung thermodynamischer Prozesse
3.3.6 Stationärer Fließprozess
3.3.7 Energiebilanz bei Mischung feuchter Luft
40
3.3.6 Stationärer Fließprozess in offenen Systemen
•
Annahmen:
Stationär  Masse und Gesamtenergie im System konstant:
41
Bilanz am stationären offenen System
• 1. Hauptsatz
Energie mit
Massenstrom
• Einsetzen der Totalenthalpien
• Spezifisch mit Arbeit und Wärmestrom auf Massenstrom bezogen
42
Beispiel: Kühlschrank
• 1. Hauptsatz geschlossenes System, stationär:
Gesamtsystem
• Prozessbewertung durch Leistungszahl:
Bestimmung von Arbeit- und Wärmestromes an geeigneten (Teil)-Systemen
43
Bilanz am Kompressor
System Kompressor
• 1. Hauptsatz offenes System, stationär und adiabat:
• Annahme Dekin = Depot  0:
44
Bilanz am Verdampfer
System Verdampfer
• 1. Hauptsatz offenes System, stationär:
• Annahme Dekin = Depot  0 :
 Leistungszahl:
45
Bilanz am Kondensator
Gesamtsytem
System Kondensator
•1. Hauptsatz, offenes System, stationär, Δekin = Δ epot  0:
•Oder aus Bilanz am Gesamtsystem, stationär
( Es folgt:
46
)
Bilanz an der Drossel
System Drossel
•
1. Hauptsatz offenes System, stationär, adiabat, Δekin = Δepot  0:
Adiabate Drossel ist isenthalp!
47
T,v - Diagramm
•
Drücke p1 und p2 werden so
gewählt, dass
T3 > TRaum
T4 < TKühlschrank
•
In der Drossel soll mit Druck auch Temperatur absinken
-
Mit Joule-Thomson-Koeffizient
(siehe Thermo II)
 Kühlmittel μ > 0
•
Regeneration zur Erhöhung der Kapazität
48
p,h-Digramm zur Analyse von Kältemaschine/Wärmepumpe
p2
p1
49
3
4
2
1
Leistungszahl
•
Aus Tabellen (aus h-p Diagramm) für Kältemittel R134a:
h1 = 231,4 (380) kJ/kg
h2 = 280,2 (430) kJ/kg
h3 = h4 = 105,3 (255) kJ/kg
 e = 2,58
•
Kühlleistung ist damit um Faktor 2,58 höher als eingesetzte Leistung!
•
Energie wird zur Verschiebung der thermischen Energie eingesetzt!
50
Beispiel: Elektrische Heizung
•
1. Hauptsatz geschlossenes System
•
Leistungszahl:
•
Heizen mit Strom ineffizient, da Wirkungsgrad der Stromerzeugung im Kraftwerk
hKW  40 %, so dass Gesamtleistungszahl
51
Beispiel: Konventionelle Heizung
•
Wärmeleistung
Energie
•
1. Hauptsatz geschlossenes System
aus chemischer
für stationäre Verhältnisse im Haus
•
(In der Heizung wird gespeicherte chemische Energie in Wärme überführt 
dEH/dt ≠ 0)
•
Leistungszahl:
52
Beispiel: Heizung mit elektrischer Wärmepumpe
Prinzip:
• Umgekehrter Kühlschrank
-
Eisfach draußen
-
Kondensator im Haus
• Eisfachtemperatur muss kälter sein
als Außentemperatur
Analyse:
• 1. Hauptsatz geschlossenes System für stationäre
Verhältnisse im Haus
53
Beispiel: Heizung mit elektrischer Wärmepumpe
•
Leistungszahl:
•
Mit Zahlenwert für Kühlschrank:
•
Berücksichtigung der Stromerzeugung:
•
Wärmepumpe sehr viel effizienter als konventionelle Heizung, aber
kompliziertere Gerätetechnik
54