Arbeit - Energie - Reibung - mathe-physik

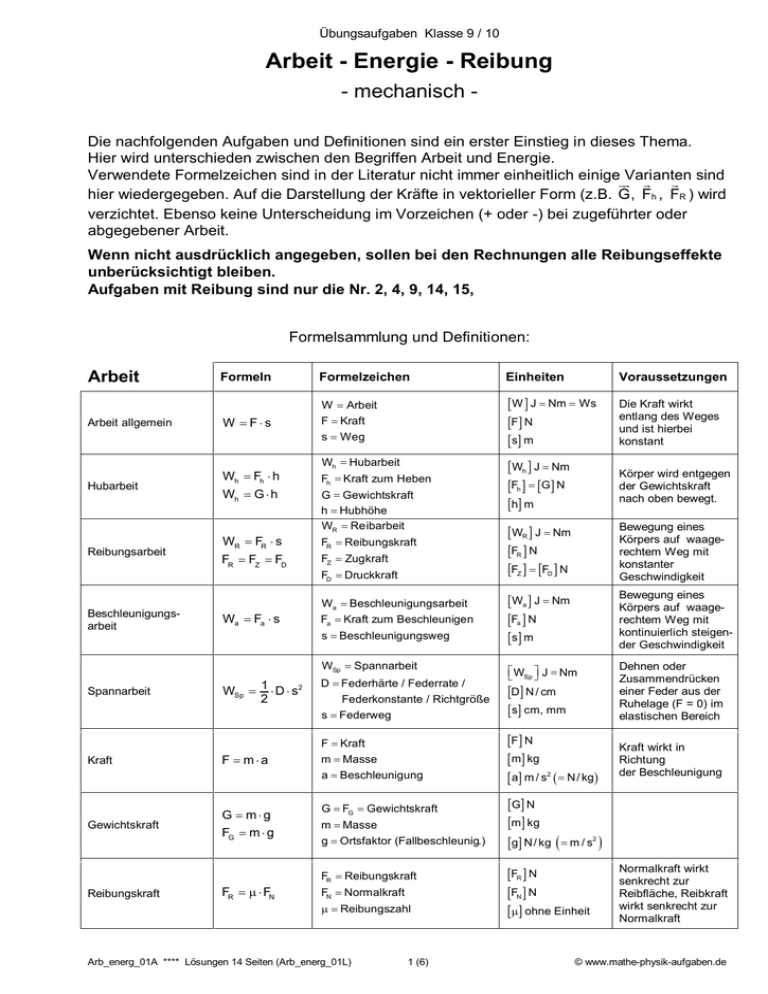
Übungsaufgaben Klasse 9 / 10
Arbeit - Energie - Reibung
- mechanisch Die nachfolgenden Aufgaben und Definitionen sind ein erster Einstieg in dieses Thema.
Hier wird unterschieden zwischen den Begriffen Arbeit und Energie.
Verwendete Formelzeichen sind in der Literatur nicht immer einheitlich einigeτθVarianten
θ θ sind
hier wiedergegeben. Auf die Darstellung der Kräfte in vektorieller Form (z.B. G, Fh , FR ) wird
verzichtet. Ebenso keine Unterscheidung im Vorzeichen (+ oder -) bei zugeführter oder
abgegebener Arbeit.
Wenn nicht ausdrücklich angegeben, sollen bei den Rechnungen alle Reibungseffekte
unberücksichtigt bleiben.
Aufgaben mit Reibung sind nur die Nr. 2, 4, 9, 14, 15,
Formelsammlung und Definitionen:
Arbeit
Arbeit allgemein
Hubarbeit
Reibungsarbeit
Beschleunigungsarbeit
Formeln
Formelzeichen
Einheiten
Voraussetzungen
W < F√s
W < Arbeit
F < Kraft
s < Weg
Ζ W ∴ J < Nm < Ws
ΖF∴ N
Ζ s∴ m
Die Kraft wirkt
entlang des Weges
und ist hierbei
konstant
Ζ Wh ∴ J < Nm
ΖFh ∴ < ΖG∴ N
Ζh∴ m
Körper wird entgegen
der Gewichtskraft
nach oben bewegt.
Ζ WR ∴ J < Nm
ΖFR ∴ N
ΖFZ ∴ < ΖFD ∴ N
Bewegung eines
Körpers auf waagerechtem Weg mit
konstanter
Geschwindigkeit
Ζ Wa ∴ J < Nm
ΖFa ∴ N
Ζs ∴ m
Bewegung eines
Körpers auf waagerechtem Weg mit
kontinuierlich steigender Geschwindigkeit
 WSp  J < Nm
ΖD∴ N / cm
Dehnen oder
Zusammendrücken
einer Feder aus der
Ruhelage (F = 0) im
elastischen Bereich
Wh < Hubarbeit
Wh < Fh √ h
Fh < Kraft zum Heben
Wh < G √ h
G < Gewichtskraft
h < Hubhöhe
WR < Reibarbeit
WR < FR √ s
FR < Reibungskraft
FR < FZ < FD
FZ < Zugkraft
Wa < Fa √ s
FD < Druckkraft
Wa < Beschleunigungsarbeit
Fa < Kraft zum Beschleunigen
s < Beschleunigungsweg
WSp < Spannarbeit
Spannarbeit
WSp <
1
√ D √ s2
2
Kraft
F < m√a
Gewichtskraft
G < m√g
FG < m √ g
D < Federhärte / Federrate /
Federkonstante / Richtgröße
s < Federweg
F < Kraft
m < Masse
a < Beschleunigung
G < FG < Gewichtskraft
m < Masse
g < Ortsfaktor (Fallbeschleunig.)
FR < Reibungskraft
Reibungskraft
FR < λ √ FN
FN < Normalkraft
λ < Reibungszahl
Arb_energ_01A **** Lösungen 14 Seiten (Arb_energ_01L)
1 (6)
Ζs∴ cm, mm
ΖF∴ N
Ζm∴ kg
Ζ a∴ m / s2 ∋ < N / kg(
Kraft wirkt in
Richtung
der Beschleunigung
ΖG∴ N
Ζm∴ kg
Ζg∴ N / kg ∋ < m / s2 (
ΖFR ∴ N
ΖFN ∴ N
Ζλ∴ ohne Einheit
Normalkraft wirkt
senkrecht zur
Reibfläche, Reibkraft
wirkt senkrecht zur
Normalkraft
© www.mathe-physik-aufgaben.de
Übungsaufgaben Klasse 9 / 10
Arbeit - Energie - Reibung
- mechanisch -
Energie
Höhenenergie
Potentielle Energie
Lageenergie
Formeln
Spannenergie
Einheiten
Epot < Höhenenergie
Epot  J < Nm
ΖG∴ N
Epot < G √ h
Epot < m √ g √ h
Ekin
Bewegungsenergie
Kinetische Energie
Formelzeichen
< 1 m √ v2
2
m < Masse des Körpers
G < Gewichtskraft
h < Höhe über Bezugsniveau
g < Ortsfaktor
Ζm∴ kg
Ζh∴ m
Ζg∴ N / kg ∋ < m / s2 (
Ekin < Bewegungsenergie
Epot  J < Nm
Ζ G∴ N
m < Masse des Körpers
v < Geschwindigkeit
Ekin < Fa √ s
Fa < Kraft zum Beschleunigen
Ekin < m √ a √ s
s < Beschleunigungsweg
a < Beschleunigung
ESp <
1
√ D √ s2
2
Voraussetzungen
ESp < Spannenergie
D < Federhärte / Federrate
s < Federweg
Ζm∴ kg
Ζ h∴ m
Ζ a∴ m / s2 ∋ < N / kg(
Durch Hubarbeit
entstandene Energie.
Entspricht der
Hubarbeit zum
Anheben einer Masse
vom Bezugsniveau auf
die Höhe h.
G < m √ g ist konstant
bzw. vernachlässigbar
Beschleunigung eines
Körpers aus der
Ruhelage (Beschleunigungsarbeit), oder
ein Körper bewegt sich
mit der Geschwindigkeit v.
Dehnen oder
Zusammendrücken
einer Feder aus der
Ruhelage (F = 0) im
elastischen Bereich
ESp  J < Nm
ΖD∴ N / cm
Ζ s∴ cm, mm
Umrechnungen / Konstanten:
1Nm < 1 J < 1 Ws (Wattsekunde)
kg √ m
s2
g ≡ 9,81 m2 Fallbeschleunigung
s
g ≡ 9,81 N Ortsfaktor
kg
1N < 1
g < 9,80665 m2
s
Normfallbeschleunigung (Beschleunigung am Normort)
Arb_energ_01A **** Lösungen 14 Seiten (Arb_energ_01L)
2 (6)
© www.mathe-physik-aufgaben.de
Übungsaufgaben Klasse 9 / 10
Arbeit - Energie - Reibung
- mechanisch 1.
Wie groß ist die Arbeit (kJ) die verrichtet wird, wenn ein Gepäckträger einen Sack
der Masse 85 kg vom Boden auf eine Rampe der Höhe 80 cm hebt?
2.
Welche Arbeit wird verrichtet, wenn ein Gepäckstück (m = 20 kg) auf einem Rollwagen
der Gewichtskraft 450 N ( λ < 0,15 ) auf ebenem Bahnsteig 30 m weit gezogen wird?
3.
Das Gepäckstück aus Aufgabe 2 muss ins Gepäckabteil eines InterCity umgeladen
werden. Dazu wird es vom Rollwagen (Ladehöhe 1,20 m) in den Gepäckraum des
InterCity (Stauhöhe 45 cm) abgeladen.
Welche Arbeit erfordert das Umladen?
4.
Ein LKW der Masse 4,6 t fährt auf ebener Strecke mit konstanter Geschwindigkeit.
Die Fahrtstrecke beträgt 1,3 km. Der Reibungswiderstand (Betrag der Reibkraft)
zwischen Reifen und Fahrbahn ist 4 % des Gesamtgewichtes (Betrag der Gewichtskraft) des LKW.
Welche Arbeit wird zum Fahren aufgewendet, wenn nur die Reibung zwischen Reifen
und Fahrbahn berücksichtigt wird?
5.
Bei einem Experiment wird ein Körper auf waagerechter Unterlage mit einer konstanten
Kraft von 6 N die Strecke 40 cm weit bewegt. Die Kraft wirkt parallel zum Weg.
Zeichne ein Kraft-Weg-Diagramm.
Berechne die zu verrichtende Arbeit.
Beschreibe die Bedeutung der Arbeit im Kraft-Weg-Diagramm.
6.
Mit einem Kran wird eine Bronzefigur der Masse 2,5 t auf einen 12 m hohen Sockel
gehoben.
Welche Energieform hat die Figur dadurch erhalten? Wie groß ist diese Energie (MJ)?
7.
Ein PKW der Masse 1,5 t fährt mit der konstanten Geschwindigkeit 130 km / h.
Berechne seine kinetische Energie. Nach Abbremsen des Fahrzeugs auf 30 km / h
besitzt der PKW eine geringere Bewegungsenergie.
Wie viel kJ wurden durch den Bremsvorgang verbraucht (umgewandelt)?
8.
Eine Rangierlokomotive der Masse 12,5 t wird durch die konstante Kraft 1,5 kN entlang
der Schiene aus der Ruhelage heraus beschleunigt. Die Beschleunigungsstrecke
beträgt 0,6 km.
a) Wie groß ist die verrichtete Beschleunigungsarbeit?
b) Welche Endgeschwindigkeit erreicht die Lok nach dem Beschleunigen?
c) Wie groß ist dann die kinetische Energie?
d) Auf welche Höhe könnte man mit dieser kinetischen Energie die Lok anheben?
Arb_energ_01A **** Lösungen 14 Seiten (Arb_energ_01L)
3 (6)
© www.mathe-physik-aufgaben.de
Übungsaufgaben Klasse 9 / 10
Arbeit - Energie - Reibung
- mechanisch 9.
10.
Malte fährt mit seinem Auto (m = 1,4 t) auf der Autobahn. Die Reisegeschwindigkeit
beträgt 135 km/h. Plötzlich taucht in 160 m Entfernung das Ende eines Staus auf und
Malte bremst den Wagen ab. Die Bremsen üben auf das Fahrzeug eine konstante
Bremskraft vom Betrag 6,2 kN aus.
Kommt Malte noch vor dem Hindernis zum Stehen?
In einem Versuchsaufbau lässt man eine kleine Kugel der Masse m mit der
Geschwindigkeit 2,2 m/s horizontal gegen eine schiefe Ebene anlaufen.
Das obere Höhenniveau liegt 25 cm über der Basis-Lauffläche.
Kann die Kugel das obere Höhenniveau erreichen?
Die kinetische Energie durch die Drehbewegung der Kugel (Rotationsenergie)
soll unberücksichtigt bleiben.
11.
Um die Zerstörungen zu demonstrieren, die bei einem Auffahrunfall eines Autos
auftreten, wird ein Auto an einem Seil 5 m hoch gehoben und anschließend aus
dieser Höhe auf Beton fallen gelassen. Die Verformungen am Auto sind ebenso groß,
als wenn das Fahrzeug gegen eine Betonmauer gefahren wäre.
Berechne die Geschwindigkeit mit der das Auto gegen die Betonmauer fahren müsste.
12.
Die Kugel (m = 150 g) des nebenstehend
skizzierten Fadenpendels wird am straff
gespannten Faden ausgelenkt (A) und
dabei auf die Höhe h = 25 cm angehoben.
Nach Loslassen der Kugel schwingt sie
20 Perioden und erreicht anschließend
nur noch eine Höhe von 21 cm.
a) Beschreibe die Energieumwandlungen
von A nach B sowie von B nach C.
b) Berechne den Verlust an mechanischer
Energie nach 20 Perioden.
c) Ermittle die Geschwindigkeit der Kugel
im Punkt B (Nulldurchgang) während
der ersten Periode (bis dahin auftretende
Verluste an mech. Energie können
vernachlässigt werden).
Arb_energ_01A **** Lösungen 14 Seiten (Arb_energ_01L)
4 (6)
© www.mathe-physik-aufgaben.de
Übungsaufgaben Klasse 9 / 10
Arbeit - Energie - Reibung
- mechanisch 13.
Harry der Elektromonteur (m = 85 kg) klettert den Mast einer Starkstromleitung hinauf
um die Befestigung der Leitungen zu überprüfen. Das Werkzeug das er mitnimmt wiegt
insgesamt 13 kg. Beim Hinaufsteigen verrichtet der Monteur eine Hubarbeit (an sich
und seiner Ausrüstung) von 11,5 kJ.
Wie hoch ist der Monteur aufgestiegen?
14.
Ein Motorrad der Masse 180 kg wird wegen eines Getriebeschadens auf dem
waagerechten Hof einer Werkstatt zu der 15 m entfernten Hebebühne geschoben.
Dazu ist eine Kraft (parallel zum Weg) vom Betrag 250 N erforderlich.
Auf der Hebebühne angekommen wird das Motorrad 1,8 m angehoben wo es dann für
die Reparatur 3 Stunden verbleibt.
Welche Arbeit wurde insgesamt am Motorrad verrichtet?
15.
Florentyna zieht einen Schlitten, auf dem ihre beiden Kinder Jens und Uwe sitzen,
mit der Kraftkomponente 110 N parallel zum Untergrund.
a) Gelingt es Florentyna den Schlitten in Bewegung zu setzen? Rechnerische
Begründung!
b) Uwe springt nun vom Schlitten herunter. Welche Kraft muss Florentyna jetzt
aufwenden, um den Schlitten mit konstanter Geschwindigkeit zu ziehen?
Gegebene Werte:
mSchlitten < 8 kg, mJens < 45 kg, mUwe < 52 kg, λHaft < 0,15, λGleit < 0,02
16.
Gleich schwere Flaschen sind vom Boden aus in die jeweiligen Fächer eines Regals
gehoben worden. In welchen Fällen wurde die gleiche Arbeit zum Füllen der Regalfächer verrichtet? Antwortbeispiel: W1C < W4D
Gib eine kurze Begründung an!
Arb_energ_01A **** Lösungen 14 Seiten (Arb_energ_01L)
5 (6)
© www.mathe-physik-aufgaben.de
Übungsaufgaben Klasse 9 / 10
Arbeit - Energie - Reibung
- mechanisch 17.
Eine Kugel der Masse 0,5 kg wird mit einer Vorrichtung vom Boden aus senkrecht
nach oben geschossen. Sie erreicht eine Höhe von 8 m.
a) Beschreibe die Energieumwandlungen vom Abschuss bis die Kugel am Boden
auftrifft.
b) Wie groß ist die Lageenergie (potenzielle Energie) der Kugel im höchsten Punkt
ihrer Bahn?
c) Mit welcher Geschwindigkeit trifft die Kugel am Boden auf?
d) Aus welcher Höhe müsste die Kugel herabfallen, damit sie nur halbe Geschwindigkeit erreicht?
18.
Die Pumpe eines kleinen Wasserwerks befördert 20 000 Liter Wasser
( θ Wasser < 1kg / dm3 ) in ein 40 m höher gelegenes Speicherbecken.
Berechne die Lageenergie, die das hoch gepumpte Wasser gegenüber dem
ursprünglichen Ort hat.
19.
Um eine ungespannte Zugfeder von L0 = 80 mm auf L1 = 95 mm zu verlängern,
ist eine Kraft von vom Betrag 45 N notwendig.
a) Berechne die Federkonstante (Richtgröße).
b) Welche Kraft muss auf die Feder wirken, wenn sie um 8 mm verlängert
werden soll?
c) Welche Arbeit ist an der ungespannten Feder zu verrichten um sie auf 100 mm
zu verlängern?
d) Zeichne das Kraft-Weg-Diagramm für diese Feder.
Welche physikalische Bedeutung hat die Steigung in diesem Diagramm?
e) Begründe mit Hilfe des Kraft-Weg-Diagramms, warum zur Bestimmung der
Spannarbeit die Gleichung W < F √ s falsch ist.
20.
Eine Druckfeder wird durch die Kraft F1 = 50 N vorgespannt. Durch vergrößern der
Kraft um 20 N wird die Druckfeder um 12 cm zusammengedrückt.
Welche Arbeit ist für diese zusätzliche Dehnung nötig?
21.
Eine Feder ist durch die Kraft F1 = 15 N vorgespannt. Wie groß ist die Endkraft, wenn
für ein weiteres Spannen um 10 cm die Arbeit 2,5 J erforderlich ist?
Arb_energ_01A **** Lösungen 14 Seiten (Arb_energ_01L)
6 (6)
© www.mathe-physik-aufgaben.de
Übungsaufgaben
Arbeit, Leistung, Wirkungsgrad
- mechanisch 1.
Ein Koffer mit der Gewichtskraft FG = 280 N wird vom Hauseingang in die 12 m höher
gelegene Wohnung und dort dann 8 m ins Wohnzimmer getragen.
Wie groß ist die aufzuwendende Arbeit (am Koffer) ?
2.
Wie groß ist die Hubarbeit, wenn ein Materialaufzug Steine mit einer Gewichtskraft
FG = 8,0 kN die Strecke 6,0 m senkrecht nach oben befördert ?
3.
Berechne die Reibungsarbeit an einem Wagen mit einer Gewichtskraft FG = 1,5 kN,
der auf einer waagrechten Straße ( µ = 0,09) 300 m gezogen wird ?
4.
An der Deichsel eines Handwagens, die mit der Waagrechten einen Winkel α = 25°
bildet, greift eine Kraft F = 150 N an. Welche Reibungsarbeit wird verrichtet, wenn der
Wagen 200 m auf waagrechter Straße gezogen wird ?
5.
Ein Schnellbahnzug fährt auf ebenem Gleiskörper mit konstanter Geschwindigkeit. Die
gesamte Gewichtskraft des Zuges beträgt 3,5 . 106 N.
a) Welche Arbeit muss das Triebwerk auf der Strecke von 33 km verrichten, wenn
der gesamte Fahrtwiderstand 0,5 % der Gewichtskraft beträgt ?
b) Welche Leistung bringt der Antrieb, wenn der Zug die Strecke in der Zeit von
20 Minuten zurücklegt ?
6.
Ein Triebwagen hat die Masse m = 85 t. Er fährt mit konstanter Geschwindigkeit eine
12 km lange Bergstrecke hinauf und gewinnt dabei eine Höhe von 44 m.
Der Fahrtwiderstand beträgt 0,5 % der Gewichtskraft. (Ortsfaktor g = 9,81 N/kg)
Welche Arbeit muss das Triebwerk verrichten ?
7.
Ein Stahlrohr mit der Gewichtskraft FG = 670 N wird mit einem Flaschenzug
(insgesamt 6 Rollen; FG,lose Rolle = 50 N) auf eine 3,0 m hohe Rampe gehoben.
Am freien Seilende muss dazu eine Zugkraft FZ = 135 N angreifen.
Welchen Wirkungsgrad hat der Flaschenzug ?
8.
Auf ebenem Boden stehen 8 gleiche, steinerne Zylinder nebeneinander. Jeder Steinzylinder hat die Höhe h1 = 0,35 m und die Gewichtskraft FG = 920 N. Aus diesen
8 Zylindern wird eine h = 2,80 m hohe Säule zusammengestellt.
Welche Arbeit muss dabei aufgewendet werden ?
9.
Welche Leistung (in kW) muss der Motor einer Hebebühne zum Anheben von Kraftfahrzeugen haben, wenn eine Last mit der Gewichtskraft 12 kN in der Zeit t = 15 s um
1,75 m angehoben werden soll ?
Arblei_01A **** Lösungen 12 Seiten (Arblei_01L)
1 (4)
www.mathe-physik-aufgaben.de
Übungsaufgaben
Arbeit, Leistung, Wirkungsgrad
- mechanisch 10.
Ein Wanderer, der mit Rucksack die Gewichtskraft 880 N hat, überwindet einen
Höhenunterschied von 1 000 m in 200 Minuten.
Wie groß ist die durchschnittliche Leistung des Wanderers ?
11.
Welche Zeit braucht ein Radfahrer, der zusammen mit seinem Rad die Masse
m = 78 kg hat, um einen Höhenunterschied von 450 m zu überwinden, wenn seine
Durchschnittsleistung 70 W beträgt ?
12.
Ein Lastkran wird mit einem Motor von 5 600 W Leistungsaufnahme betrieben. Er hebt
eine Last mit der Masse m = 2,5 t in der Zeit t = 1 min um 8,2 m an.
In welchem Verhältnis steht die vom Motor aufgenommene Leistung zur Nutzleistung
(Wirkungsgrad η ) ?
13.
Der Motor einer Seilwinde leistet 8,0 kW.
Welche Masse kann mit dieser Seilwinde in 1,5 min um 30 m gehoben werden ?
14.
Der Motor einer Seilwinde leistet 1,5 kW.
In welche Höhe kann diese Seilwinde eine Masse von 250 kg in 2,5 min befördern ?
15.
Der Motor eines Liftes leistet 12 kW. Das Eigengewicht des Liftes beträgt 3,25 kN.
Wieviel Personen (je 75 kg) kann dieser Lift in 15 Sekunden 18 m in die Höhe
befördern ?
16.
Um einen Motorblock der Masse 0,36 t um 2,0 m zu heben, verwendet ein Mechaniker
einen Flaschenzug mit 6 Rollen. Während des Hubvorganges, der 20 s dauert, muss
er mit einer Kraft von 650 N ziehen.
a) Berechne die Arbeit des Mechanikers und die Hubarbeit am Motorblock.
b) Wie groß ist der Wirkungsgrad des Flaschenzuges ?
c) Welche Leistung erbringt der Mechaniker während des Hubvorganges ?
17.
Um einen Steinquader der Masse 440 kg um 1,5 m zu heben, verwendet ein Arbeiter
einen Flaschenzug mit 8 Rollen. Er muss dabei mit einer Kraft von 0,60 kN ziehen.
Er leistet während des Hubvorganges 400 W.
a) Berechne die Zeit, die der Arbeiter für den Hubvorgang benötigt.
b) Berechne den Wirkungsgrad des Flaschenzuges.
c) Wie heißt eine Maschine mit einem Wirkungsgrad größer als 100 % ?
Arblei_01A **** Lösungen 12 Seiten (Arblei_01L)
2 (4)
www.mathe-physik-aufgaben.de
Übungsaufgaben
Arbeit, Leistung, Wirkungsgrad
- mechanisch 18.
Eine Pumpe hat eine Leistung von P = 125 kW. Wie viele Kubikmeter Wasser kann sie
in 24 Stunden aus einem 200 m tiefen Brunnen herauspumpen ?
Die dabei auftretende Reibung wird nicht berücksichtigt.
Dichte des Wassers: ρ W = 1,0 kg / dm3
19.
Zur Versorgung einer Gemeinde sind aus einem Brunnen in 24 Stunden 1 250 m3
Wasser aus einer Tiefe von 230 m an die Oberfläche zu pumpen. Der Wirkungsgrad
der Pumpe mit Rohrnetz (Reibungsverluste) beträgt 0,72.
Berechne die erforderliche Antriebsleistung des Motors !
Dichte des Wassers: ρ W = 1,0 kg / dm3
20.
Eine Pumpe drückt Wasser durch eine Rohrleitung auf 50 m Höhe mit einem
Wirkungsgrad von 0,77.
Berechne die Wassermenge, die mit einer Pumpen-Antriebsleistung von 44 kW
stündlich gefördert werden kann ! Dichte des Wassers: ρW = 1,0 kg / dm3
21.
Die menschliche Dauerleistung ist etwa 75 W. Mit dieser Leistung schaufelt ein
Arbeiter während einer Zeit t = 30 min ohne Unterbrechung Kies auf einen
Lastwagen.
Welchem Geldwert entspricht diese menschliche Arbeit, wenn man den Tarif der
Elektrizitätswerke von 0,23 Euro je kWh zugrunde legt ?
22.
Beim Verladen von Kraftfahrzeugen zieht ein Hafenkran einen Pkw der Masse
m = 950 kg hoch; dabei bewegt sich der Pkw mit der Geschwindigkeit v = 2,4 m/s
aufwärts.
a) Berechne die Gewichtskraft FG des Pkw ! (Ortsfaktor g = 9,81 N/kg)
b) Berechne die Hubleistung P, die der Elektromotor des Krans für die genannte
Arbeitsverrichtung abgeben muss !
23.
Über den kanadischen Niagarafall stürzt in jeder Sekunde die Wassermasse
m = 20 000 t die Fallhöhe h = 48,2 m hinab.
a) Es soll angenommen werden, das man die gesamte Leistung Pges des fallenden
Wassers technisch gewinnen könnte. Berechne diese Leistung !
b) In Wirklichkeit wird nur die Leistung P = 2 200 MW industriell genutzt.
Wieviel Prozent der unter a) berechneten Gesamtleistung wird also genutzt ?
(Ortsfaktor g = 9,81 N/kg)
Arblei_01A **** Lösungen 12 Seiten (Arblei_01L)
3 (4)
www.mathe-physik-aufgaben.de
Übungsaufgaben
Arbeit, Leistung, Wirkungsgrad
- mechanisch 24.
Eine Wasserpumpe fördert eine Wassermenge von 60 m3 in 10 min auf eine Höhe von
7 m. Dabei nimmt der Antriebsmotor eine Leistung von 11,5 kW aus dem Netz auf.
Sein Wirkungsgrad beträgt 0,85.
Berechne:
a) den Gesamtwirkungsgrad der Anlage
b) den Wirkungsgrad der Pumpe mit Rohrleitung
Arblei_01A **** Lösungen 12 Seiten (Arblei_01L)
4 (4)
www.mathe-physik-aufgaben.de
Übungsaufgaben
Dichte 1
1.
Wie schwer sind auf dem Jupiter 3 ml Benzin ?
(Dichte von Benzin: ρB = 0,8 kg/dm3 ;
Fallbeschleunigung = Ortsfaktor auf dem Jupiter: g = 26 m/s2 )
2.
Entscheide durch Rechnung, ob ein Goldwürfel der Kantenlänge 3,0 cm und der
Gewichtskraft 3,5 N massiv ist, d.h. aus reinem Gold besteht !
(Dichte von Gold: ρAu = 19,3 g/cm3 )
3.
Das rechteckige Flachdach eines Hauses ist 18 m lang und 9 m breit. Nach starkem
Schneefall ist es mit einer 20 cm hohen Schneeschicht bedeckt.
(Dichte des Schnees: ρSchnee = 0,2 g/cm3 )
a) Welche Masse hat die Schneeschicht ?
b) Welche zusätzliche Last muß das Dach aufnehmen ?
4.
Ein Messingwürfel (FG = 2,2 N) erzeugt in einem in ml (Milliliter) geeichten
Messzylinder einen Anstieg des Wasserspiegels vom 40. zum 67. Skalenteil.
a) Berechne die Dichte von Messing !
b) Begründe, ob ein gleich schwerer Silberwürfel größeres oder kleineres Volumen
hat ! Berechne es !
5.
Ein kleiner, ganz mit Wasser gefüllter Glaskolben (Pyknometer) hat die Masse
126,8 g. Man bringt ein Metallstück der Masse 5,26 g in den Kolben, wodurch ein
bestimmtes Wasservolumen austritt.
Die Masse des Kolbens ist nun 131,34 g.
a) Berechne die Dichte das Metallstücks !
b) Berechne die Gewichtskraft des Metallstücks auf dem Mond !
(Fallbeschleunigung = Ortsfaktor auf dem Mond: g = 1,6 N / k g)
6.
Würden Astronauten auf dem Mars landen, könnten sie einen Gesteinsbrocken
aufnehmen und seine Masse m und seine Gewichtskraft FG messen.
Wie groß ist die Fallbeschleunigung (Ortsfaktor) g für folgende Meßergebnisse:
m = 12,6 kg und FG = 47,4 N ?
7.
Ein Körper hängt an einer Federwaage. Auf dem Jupiter (g = 26,0 N / k g) würde sie
156 N anzeigen, auf einem unbekannten Himmelskörper dagegen 4,8 N.
Wie groß ist die Fallbeschleunigung (Ortsfaktor) g auf dem unbekannten Himmelskörper ?
8.
Ein Wetterballon besitzt am Erdboden die Gewichtskraft FG,0 = 1240 N.
An der Erdoberfläche ist die Fallbeschleunigung (Ortsfaktor) g0 = 9,81 m/s2;
in 10 km Höhe über dem Erdboden ist die Fallbeschleunigung g1 = 9,50 m/s2.
a) Berechne die Masse des Ballons !
b) Berechne die Gewichtskraft FG,1 , die der Ballon in 10 km Höhe besitzt !
Dichte_01A **** Lösungen 4 Seiten (Dichte_01L)
1 (1)
www.mathe-physik-aufgaben.de
Übungsaufgaben
Dichte 2
1.
Ein Quader hat die Maße: l = 0,634 m, b = 9,27 dm, h = 14,5 cm.
Seine Gewichtskraft beträgt an einem Normort FG = 6,50 kN.
Berechne die Dichte des Quaders.
2.
Die Gewichtskraft eines Körpers beträgt auf dem Jupiter 0,75 kN.
Welche Masse würde man bei diesem Körper auf dem Mond messen ?
(Fallbeschleunigungen (Ortsfaktoren): Jupiter gJ = 26 N / kg; Mond gM = 1,6 N / kg)
3.
Ein Stoff hat an einem Normort die Dichte 3,7 kg / dm3 .
Welches Volumen haben 4,85 t dieses Stoffes ?
4.
Welche Querschnittsfläche hat ein 0,5 km langer Kupferdraht von 133,8 N Gewichtskraft ?
(Dichte von Kupfer: ρCu = 8,9 kg / dm3 )
5.
Weise durch Rechnung nach, ob man 600 g Alkohol in eine 0,70 l - Flasche füllen
kann !
(Dichte von Alkohol: ρA = 0,8 kg / dm3 )
6.
Eine Flasche besteht aus 625 cm3 Glas. Ihre Gewichtskraft beträgt leer 20 N,
vollständig mit Wasser gefüllt 78 N und vollständig mit Petroleum gefüllt 63,2 N.
(Dichte von Wasser: ρW = 1,0 kg / dm3 )
a) Berechne die Dichte des Glases !
b) Berechne die Dichte des Petroleums !
c) Berechne die Gewichtskraft der Flasche mit vollständiger Quecksilberfüllung !
(Dichte von Quecksilber: ρHg = 13,4 kg / dm3 )
Dichte_02A **** Lösungen 3 Seiten (Dichte_02L)
1 (1)
www.mathe-physik-aufgaben.de
Übungsaufgaben
Dichte 3
1.
250 cm3 Marmor haben eine Masse von 650 g.
Wie groß ist die Dichte des Marmors ?
2.
Welche Masse besitzen 50 l Benzin ?
(Dichte von Benzin: ρB = 0,7 g / cm3 )
3.
Die Massen zweier Kugeln A und B sind: mA = 2,45 kg; mB = 0,98 kg.
Die Volumina der Kugeln sind: VA = 3 500 cm3; VB = 1 400 cm3.
Prüfe durch Rechnung, ob beide Kugeln aus dem gleichen Material hergestellt
sein könnten !
4.
Ein Körper A hat das zweifache Volumen und die halbe Masse des Körpers B.
Welches Verhältnis besteht zwischen den Dichten der Körper A und B ?
5.
Eine Messflasche nimmt bei vollständiger Füllung mit einer Flüssigkeit genau
V = 10 cm3 Flüssigkeit auf. Mit Hilfe einer solchen Messflasche soll die Dichte von
Benzin bestimmt werden.
Die Messflasche hat leer die Masse m1 = 35,7 g, mit Benzin vollständig gefüllt die
Masse m2 = 42,9 g.
Berechne die sich aus den Messwerten ergebende Dichte von Benzin !
6.
Die Tragfähigkeit eines Lkw beträgt 25 000 kg. Die Ladefläche des Lastkraftwagens ist
A = 21,3 m2. Der Lkw soll mit Sand beladen werden ( ρ = 1,6 g / cm3 )
a) Berechne das maximale Sandvolumen das der Lkw aufnehmen darf, wenn die
Tragfähigkeit nicht überschritten werden soll !
b) Berechne die Höhe h, die der Sand auf der Ladefläche einnimmt, wenn die
Sandoberfläche eine waagerechte Ebene bildet !
7.
Wie dick ist eine Bleiplatte, die bei gleicher Grundfläche die gleiche Masse hat wie
eine 2 cm dicke Stahlplatte !
(Dichte von Stahl: ρSt = 7,8 g / cm3 ; Dichte von Blei: ρPb = 11,3 g / cm3 )
8.
Sterne die zur Klasse der „Weißen Zwerge“ gehören haben eine sehr hoche Dichte.
Zu ihnen gehört der Sirius B. Er hat eine Dichte von ca. 1 000 000 g / cm3 .
Welches Volumen hätte ein Mensch mit 75 kg, wenn er aus dem Material wie Sirius B
bestünde ?
Vergleiche mit dem Volumen eines Likörglases (5 cm3) !
Dichte_03A **** Lösungen 7 Seiten (Dichte_03L)
1 (2)
www.mathe-physik-aufgaben.de
Übungsaufgaben
Dichte 3
9.
Die unvorstellbare Dichte von ca. 1 000 000 t / mm3 haben sogenannte
Neutronensterne. Ihr Material besteht nur noch aus Neutronen.
Berechne das Volumen eines Menschen der Masse 75 kg , wenn er ausschließlich
aus dem Material des Neutronensterns bestünde !
10.
Ein Ring besteht aus 50 g Kupfer und 35 g Zink.
Berechne die Dichte des Rings ! Um welche Legierung könnte es sich handeln ?
(Dichte von Kupfer: ρCu = 8,9 g / cm3 ; Dichte von Zink: ρZn = 7,1g / cm3 )
11.
Welche Dichte hat Bronze, wenn sie zu 70 % aus Kupfer und zu 30 % aus Zinn
besteht ?
(Dichte von Kupfer: ρCu = 8,9 g / cm3 ; Dichte von Zinn: ρSn = 7,0 g / cm3 )
12.
Eine bestimmte Messingsorte hat eine Dichte von 8,4 g/cm3.
Wieviel Prozent Kupfer und wieviel Prozent Zink enthält sie ?
(Dichte von Kupfer: ρCu = 8,9 g / cm3 ; Dichte von Zink: ρZn = 7,1g / cm3 )
Dichte_03A **** Lösungen 7 Seiten (Dichte_03L)
2 (2)
www.mathe-physik-aufgaben.de
Übungsaufgaben
Dichte 4
1.
Ein aus einem homogenen Stoff bestehender Körper hat die Masse m und das
Volumen V.
m
Unter der Dichte ρ des homogenen Stoffes versteht man den Quotienten ρ =
V
Ist die Dichte eine ortsabhängige oder eine ortsunabhängige Größe ?
2.
Rechne in die Einheit kg/m3 um:
a) 0,0036 g / cm3
b) 18,6 kg / dm3
c)
3.
ρ = 0,04 g / m3
Rechne in die Einheit g / cm3 um:
a) 3,8 kg / m3
b) 0,3 kg / dm3
c) 130 500 g / m3
4.
Es soll die Dichte einer Graugußsorte bestimmt werden. Dazu wird ein Graugußquader
mit den Kantenlängen l = 20 cm, b = 12 cm und h = 8 cm gegossen.
Mit einer Balkenwaage wird die Masse des Quaders bestimmt; es ergibt sich
m = 14,69 kg.
Berechne die Dichte ρ dieser Graugußsorte in der Einheit kg / dm3 !
5.
Ein Messbehälter nimmt bei vollständiger Füllung mit einer Flüssigkeit genau
V = 15 cm3 Flüssigkeit auf. Mit Hilfe eines solchen Messbehälters soll die Dichte ρAlk
einer Sorte Alkohol bestimmt werden. Der Messbehälter hat leer die Masse
m1 = 40,2 g, mit Alkoholfüllung die Masse m2 = 52,1 g.
Berechne die Dichte ρAlk des Alkohols, die sich aus diesen Messwerten ergibt !
6.
Eine bestimmte Kupfersorte hat die Dichte ρ = 8,89 g / cm3 . Aus diesem Material wird
ein Würfel der Kantenlänge a = 6,5 mm hergestellt.
Berechne die Masse m des Kupferwürfels !
7.
Auf ein waagerechtes Flachdach der Fläche A = 145 m2 fällt Schnee. Man kann
annehmen daß die Schneedecke auf dem Dach gleichmäßig verteilt 20 cm hoch ist.
Vergleiche die Masse des frischen Schnees mit der Masse eines Pkw (m = 970 kg).
Wieviel dieser Pkw’s entsprechen der Schneelast auf dem Dach ?
(Dichte von frischem Schnee: ρ = 0,2 g / cm3 )
Dichte_04A **** Lösungen 5 Seiten (Dichte_04L)
1 (2)
www.mathe-physik-aufgaben.de
Übungsaufgaben
Dichte 4
8.
Berechne das Volumen V einer Platinkugel mit der Masse m = 35 g !
(Dichte von Platin: ρ = 21,45 g / cm3 )
9.
Eine Menge von Benzol hat die Masse m = 598 g.
Ist es möglich dieses Benzol in einen Behälter mit 0,65 - Liter Fassungsvermögen
einzufüllen ? Rechnung !
(Dichte von Benzol: ρ = 0,88 g / cm3 )
10.
Gold hat die Dichte ρ = 19,3 g / cm3 . Ein Goldbarrenquader ist 6,4 cm lang, 2,5 cm
breit und hat die Masse m = 604 g.
a) Berechne das Volumen V des Goldbarrens !
b) Berechne die Höhe h des Goldbarrens !
11.
Zwei rechteckige Platten haben jeweils die Länge l = 0,90 m, die Breite b = 60 cm
und die Dicke d = 25 mm.
Die eine Platte besteht aus Aluminium der Dichte ρ1 = 2,78 g / cm3 , die andere Platte
besteht aus Magnesium der Dichte ρ2 = 1,74 g / cm3 .
Berechne den Massenunterschied der beiden Platten !
12.
a) Welche Dichte hat ein Würfel der Kantenlänge 17 mm und 35,2 g Masse ?
b) Welche Masse besitzt 0,35 l Dieselöl, dessen Dichte ρ = 0,86 g / cm3 ist ?
c) Welches Volumen hat Aluminium der Masse 370 g ( ρ = 2,7 g / cm3 ) ?
d) Welche Gewichtskraft erfährt ein Alublech der Länge 3,75 m, der Breite 8,50 dm
und der Dicke 2,50 mm ? (g = 9,81 N / k g; ρ = 2,7 g / cm3 )
13.
Eine Legierung besteht aus 150 g Kupfer und 92 g Zink.
Berechne ihre Dichte ! Um welche Legierung könnte es sich handeln ?
( ρCu = 8,9 g / cm3 , ρZn = 7,1g / cm3 )
Dichte_04A **** Lösungen 5 Seiten (Dichte_04L)
2 (2)
www.mathe-physik-aufgaben.de
Übungsaufgaben
Hebel 1
1.
Ein Balken, der sich um einen Punkt drehen kann, dient als Wippe. Ein Junge mit
der Gewichtskraft 300 N sitzt 2,0 m von der Drehachse entfernt.
Wo muss ein Junge mit der Gewichtskraft 250 N sitzen, damit Gleichgewicht
herrscht?
2.
Auf einen zweiseitigen Hebel, der um eine Achse drehbar ist, wirken folgende
senkrecht nach unten gerichtete Kräfte:
Links von der Drehachse:
20 N im Abstand von 30 cm; 25 N - 20 cm; 15 N – 10 cm
Rechts von der Drehachse:
18 N – 40 cm; 12 N – 35 cm; x N – 11 cm.
Wie groß muss x sein, damit der Hebel im Gleichgewicht ist?
3.
Ein Maßstab von der Länge 1 m, dessen Gewichtskraft vernachlässigt werden kann,
soll als Hebel dienen und mit folgenden Massestücken belastet werden:
0,5 kg bei der 20 cm-Marke;
0,3 kg bei der 40 cm-Marke
0,6 kg bei der 70 cm-Marke;
0,2 kg bei der 90 cm-Marke.
Wo muss die Drehachse liegen, damit Gleichgewicht herrscht?
4.
Eine Zange kann als System aus zwei Hebeln mit der gleichen Drehachse aufgefasst
werden. Der Abstand der beiden Schneiden von der Drehachse ist a 1 = 2 cm. Die
beiden Schneiden sollen jeweils mit der Kraft F 1 = 1 200 N auf einen Nagel wirken.
Die Hand kann die beiden Zangenschenkel jeweils mit der Kraft F 2 = 180 N
zusammendrücken.
Welchen Abstand a2 haben die Angriffspunkte der Handkräfte von der Drehachse?
5.
Mit einem Schraubenschlüssel, dessen wirksamer Hebelarm a 1 = 18 cm lang ist, kann
das Drehmoment M1 = 12 Nm ausgeübt werden. Durch Aufstecken eines Rohres auf
den Schraubenschlüssel kann der Hebelarm auf 60 cm verlängert werden.
Welches Drehmoment kann jetzt ausgeübt werden, wenn mit der Hand am Ende des
verlängerten Schraubenschlüssels die gleiche Kraft ausgeübt wird wie zuvor?
6.
Ein zweiseitiger Hebel nach untenstehender Skizze ist mit den Kräften F 1 bis F5
belastet.
F1 = 10 N;
F2 = 12 N;
F3 = 16 N;
F4 = x N;
F5 = 15 N;
l1 = 50 mm
l2 = 40 mm
l3 = 20 mm
l4 = 15 mm
l5 = 45 mm
Bestimme die gesuchte
Kraft F4 damit Gleichgewicht
herrscht!
Hebel_01A **** Lösungen 3 Seiten (Hebel_01L)
1 (2)
www.mathe-physik-aufgaben.de
Übungsaufgaben
Hebel 1
7.
Eine ebene Platte liegt auf zwei Stützen auf. Am linken Ende liegt ein Steinklotz
auf der Platte.
Wie weit kann ein zweiter Klotz ans rechte Ende der Platte geschoben werden
(Maß x), damit die Platte gerade nicht kippt? Tipp: Lege den Drehpunkt richtig!
Das Eigengewicht der Platte (F3) ist zu berücksichtigen.
F1 = 250N, F2 = 800N, F3 = 150N
Hebel_01A **** Lösungen 3 Seiten (Hebel_01L)
2 (2)
www.mathe-physik-aufgaben.de
Das Hebelgesetz zur Lösung technischer Aufgaben
Es gibt einseitige Hebel, zweiseitige Hebel und Winkelhebel. Mit allen Hebeln kann man die
Größe und Richtung von Kräften ändern. In der Regel verwendet man Hebel zur
Vergrößerung von Kräften. Das Hebelgesetz findet in der Technik eine sehr weitverzweigte
Anwendung, zum Beispiel bei Bremshebeln, Pressvorrichtungen, Spanneisen, Brechstangen,
Schraubenschlüsseln, Scheren, Zangen, usw.
Die Kraft F
Die Einheit für die Kraft ist das Newton, Einheitszeichen N. 1 N ist die Kraft, die der Masse
1 kg die Beschleunigung 1 m/s² erteilt, also 1N = 1kg × 1m / s² , oder 1N = 1kg m / s² .
Liegen große Kräfte vor, dann verwendet man das Kilonewton kN. Es ist 1 kN = 1000 N. Auch
Gewichte erzeugen Kräfte. Man bezeichnet diese Kräfte als Gewichtskräfte G und setzt sie
ebenfalls in Newton ein. Wenn wir einen Körper mit der Masse m in kg am freien Fall mit der
Erdbeschleunigung g » 9,81m / s² hindern wollen, dann ist die Gewichtskraft G = m × g
erforderlich.
Bei der Lösung technischer Aufgaben mit dem Hebelgesetz sind die Kräfte F oder die
Gewichtskräfte G in Newton gegeben. Die Wirkung der Kraft am Hebel kann man nur dann
genau feststellen, wenn neben dem Betrag der Kraft F auch ihre Lage, also der Hebelarm
und ihr Richtungssinn bekannt sind. Den Richtungssinn der Kraft deutet man durch eine
Pfeilspitze an.
Das Kraftmoment oder Drehmoment M
Das Moment M entsteht aus dem Produkt Kraft F mal Hebelarm I, es ist also M = F × I .
Setzt man F in N und I in mm ein, dann erhält man das Moment M in Nmm. Im Bedarfsfalle
kann man Momente auch in Nm oder kNm angeben.
Es gibt linksdrehende und rechtsdrehende Momente. Bezugspunkt bei den jeweiligen
Aufgaben ist der Hebeldrehpunkt A.
Linksdrehende Momente sind positiv und erhalten das Vorzeichen +. Wenn vor einem
Moment kein Vorzeichen steht, dann ist das Moment immer positiv.
Rechtsdrehende Momente sind negativ und erhalten das Vorzeichen -. Das Minusvorzeichen
darf man nicht weglassen.
Das Gleichgewicht am Hebel
Der einseitige Hebel befindet sich im Gleichgewicht,
wenn für den Hebeldrehpunkt A die Summe aller
Momente = 0 ist. Man schreibt S M( A ) = 0 , also
Summe aller Momente um den Drehpunkt A = 0.
Die Kraft F1 dreht um A rechts herum, es wirkt also
das Teilmoment - F1 × I .
Die Kraft F2 dreht um A links herum, es wirkt also das Teilmoment F2 × I2 . Für das
Gleichgewicht erhält man somit S M( A ) = 0 = - F1 × I1 + F2 × I2 . Nach der Formelumstellung wird
F1 × I1 = F2 × I2 . In dieser Gleichung müssen immer drei Größen bekannt sein. Die vierte Größe
kann dann berechnet werden.
Hebel_02A **** Lösungen 5 Seiten (Hebel_02L)
1 (5)
www.mathe-physik-aufgaben.de
Das Hebelgesetz zur Lösung technischer Aufgaben
Zur Übung stellen wir die Gleichung F1 × I1 = F2 × I2 nach allen Größen um.
1. Die Kraft F1 ist unbekannt, man erhält F1 =
F2 × I2
.
I1
2. Die Kraft F2 ist unbekannt, man erhält F2 =
F1 × I1
.
I2
3. Der Hebelarm I1 ist unbekannt, man erhält I1 =
F2 × I2
.
F1
4. Der Hebelarm I2 ist unbekannt, man erhält I2 =
F1 × I1
.
F2
Greifen an einem einseitigen Hebel mehr als zwei Kräfte an, dann gilt für das Gleichgewicht
ebenfalls S M( A ) = 0 .
Für den einseitigen Hebel wird
S M( A ) = 0
= - F1 × I1 - F2 × I2 + F3 × I3 + F4 × I4
Nach der Formelumstellung erhält man
F1 × I1 + F2 × I2 = F3 × I3 + F4 × I4 .
Die letzte Gleichung sagt auch aus, dass die Summe aller rechtsdrehenden Momente
F1 × I1 + F2 × I2 gleich der Summe aller linksdrehenden Momente F3 × I3 + F4 × I4 sein muss.
Übungsaufgaben zum einseitigen Hebel
1. a)
b)
An einem Presshebel greift die Handkraft
F1 = 200 N am Hebelarm I1 = 300 mm an.
Welche Presskraft F2 wirkt im Abstand
I2 = 100 mm , wenn sich der Hebel um den
Drehpunkt A im Gleichgewicht befindet?
Berechne für den Presshebel die Kraft F1 ,
wenn der Hebel mit I1 = 400 mm und I2 = 100 mm ausgeführt wird und die
Kraft F2 = 900 N betragen soll.
Hebel_02A **** Lösungen 5 Seiten (Hebel_02L)
2 (5)
www.mathe-physik-aufgaben.de
Das Hebelgesetz zur Lösung technischer Aufgaben
2. a)
b)
3.
An dem Bremshebel greift die Fußkraft
F1 = 120 N an.
Wie groß ist die Kraft F2 im Bremsgestänge?
Der senkrechte Wirkabstand der Fußkraft F1
bis zum Drehpunkt A beträgt I1 = 320 mm .
Der senkrechte Wirkabstand der Kraft F2
beträgt I2 = 70 mm .
Berechne für den Bremshebel die erforderliche
Fußkraft F1 , wenn bei den gleichen Hebelarmen
die Kraft F2 = 600 N betragen soll.
An dem einseitigen Hebel greift die Kraft
F1 = 400 N unter dem Winkel a = 40° an.
Wie groß ist das wirksame Kraftmoment M?
4.
An dem einseitigen Hebel greift die Kraft F1
am Hebelarm I1 = 400 mm an. Die Stützkraft
an der Auflage beträgt F2 = 500 N .
Wie groß muss man den Hebelarm I2 machen,
damit das Verhältnis der Kräfte F1 : F2 = 1: 2,5 wird?
Wie groß muss F1 sein?
Hebel_02A **** Lösungen 5 Seiten (Hebel_02L)
3 (5)
www.mathe-physik-aufgaben.de
Das Hebelgesetz zur Lösung technischer Aufgaben
Der zweiseitige Hebel
Der zweiseitige Hebel befindet sich im Gleichgewicht,
wenn für den Drehpunkt A die Summe aller
Momente = 0 ist. S M( A ) = 0 = - F1 × I1 + F2 × I2 ,
daraus wird F1 × I1 = F2 × I2 .
In dieser Gleichung müssen wieder drei Größen bekannt sein. Die vierte Größe kann man
berechnen.
Wenn an einem zweiseitigen Hebel mehr als zwei
Kräfte angreifen, gilt ebenfalls S M( A ) = 0 .
Für den zweiseitigen Hebel wird also
S M( A ) = 0 = F1 × I1 - F2 × I2 - F3 × I3 ,
daraus erhält man F2 × I2 + F3 × I3 = F1 × I1 .
In dieser Gleichung müssen fünf Größen bekannt sein.
Die sechste Größe kann man berechnen.
Bei schräg angreifenden Kräften gilt als Hebelarm
immer der senkrechte Abstand von der Wirklinie
der Kraft bis in den Hebeldrehpunkt A.
Für den zweiseitigen Hebel wird also
S M( A ) = 0 = F1 × I1 - F2 × I2 + F3 × I3 - F4 × I4 ,
daraus erhält man F2 × I2 + F4 × I4 = F1 × I1 + F3 × I3 .
Diese Gleichung sagt wieder aus, dass die Summe aller
rechtsdrehenden Momente gleich der Summe aller linksdrehenden Momente sein muss.
Übungsaufgaben zum zweiseitigen Hebel
5.
In welchem Abstand I3 erzeugt die Kraft
F3 = 40 N an dem zweiseitigen Hebel
Gleichgewicht, wenn die anderen Kräfte
und Hebelarme gegeben sind?
6.
In welchem Abstand I3 erzeugt die Kraft
F3 = 40 N an dem zweiseitigen Hebel
Gleichgewicht, wenn die Kraft F3 nach
unten gerichtet wirkt!
Hebel_02A **** Lösungen 5 Seiten (Hebel_02L)
4 (5)
www.mathe-physik-aufgaben.de
Das Hebelgesetz zur Lösung technischer Aufgaben
7.
An der Kurbel eines Wellrades greift im
Abstand I1 = 320 mm die Handkraft
F1 = 220 N an.
Wie groß ist die im Seil hervorgerufene
Kraft F2 , wenn der Wellraddurchmesser
d = 150 mm beträgt?
8.
Der Konstrukteur hat den Wellraddurchmesser d auf 200 mm vergrößert, die im
Seil wirksame Kraft soll F2 = 700 N betragen. Wie groß muss jetzt die Handkraft F1
in Aufgabe 7 werden, wenn aus konstruktiven Gründen I1 : d = 2 : 1 sein soll?
Der Winkelhebel
Der Winkelhebel ist ein zweiseitiger Hebel.
Er befindet sich im Gleichgewicht, wenn für
den Hebeldrehpunkt A die Summe aller
Momente = 0 ist.
Es wird also wieder S M( A ) = 0 = - F1 × I1 + F2 × I2 .
Nach der Formelumstellung ergibt sich F1 × I1 = F2 × I2 .
9.
a)
Durch die Kombination einseitiger Hebel und
Winkelhebel kann man ein Hebelgestänge
konstruieren, bei dem die eingeleitete Kraft F1
in die Kraft F3 umgesetzt wird (Bild unten).
Wie groß ist die Kraft F3 bei den gegebenen Werten
F1 = 180 N, l1 = 530 mm, l2 = 120 mm, I3 = 180 mm, I4 = 90 mm ?
b)
Das Hebelgestänge soll F3 = 2000 N liefern. Wie groß muss der neue
Hebelarm I1 sein, wenn die eingeleitete Kraft nunmehr F1 = 200 N beträgt?
Hebel_02A **** Lösungen 5 Seiten (Hebel_02L)
5 (5)
www.mathe-physik-aufgaben.de
Übungsaufgaben
Hookesches Gesetz
1.
Kraftmesser zeigen bei einer Verlängerung um 10 cm die Kräfte 0,1N; 1N; 5N bzw.
10 N an. Berechne die jeweiligen Federkonstanten !
2.
Eine Feder wird durch 40 cN um 6 cm, durch 80 cN um 12 cm länger.
Wie stark wird sie durch 60 cN bzw. 5 cN verlängert ?
Können wir sicher angeben, um wieviel sie durch 10 N verlängert wird ?
Wieviel wiegt ein Körper, der diese Feder um 10 cm verlängert ?
3.
Rechne die Federhärte D = 10 cN / cm in N / cm um !
4.
2 Spiralfedern mit den Federkonstanten D1 = 0,5 N / cm und D2 = 2,0 N / cm werden
aneinander gehängt, so dass eine einzige Feder entsteht.
a) Um wieviel verlängert sich diese, wenn man an ihr mit einer Kraft von 1 N zieht ?
b) Berechne die Federkonstante D der Federkombination !
5.
Manche Lastwagen haben an den Hinterachsen
doppelte Federn. Die innere Feder wird erst
zusammengedrückt, wenn der Wagenkasten sich
um den Weg s gesenkt hat.
Für die äußere Feder sei D1 = 100 N / cm, für die
innere D2 = 200 N / cm; s = 10 cm.
Wie stark muss man jede Doppelfeder belasten,
damit sich der Wagenkasten um 16 cm senkt ?
Zeichne ein Senkungs-Belastungsdiagramm bis
zu 20 cm Senkung !
6.
Gegeben sind zwei Schraubenfedern. Die erste ist im unbelasteten Zustand 20 cm
lang. Sie hat eine Federhärte von 0,15 N / cm und eine Gewichtskraft von 0,25 N.
Die zweite Feder ist im unbelasteten Zustand 35 cm lang, hat eine Federhärte von
0,08 N / cm und eine Gewichtskraft von 0,20 N.
Die erste Feder hängt an einem Haken. An ihrem unteren Ende wird die zweite
Feder befestigt.
Wie lang sind beide Federn zusammen, wenn nun noch an das Ende der zweiten
Feder ein Massenstück gehängt wird, dessen Gewichtskraft 1,5 N beträgt ?
7.
Welche Gesamtlänge ergibt sich, wenn die beiden Federn der vorhergehenden
Aufgabe bei sonst gleichen Verhältnissen in umgekehrter Reihenfolge aneinander
gehängt werden ?
8.
Eine Schrauben-Zugfeder hängt vertikal an einem Haken und wird mit 1,5 N belastet.
Sie hat dann eine Gesamtlänge von 48 cm. Belastet man nun die Feder zusätzlich
mit 0,7 N, so dehnt sie sich auf insgesamt 62 cm.
a) Berechne die Federkonstante D !
b) Wie lang ist die Schraubenfeder im unbelasteten Zustand ?
Hooke_01A **** Lösungen 5 Seiten
1 (1)
www.mathe-physik-aufgaben.de
Übungsaufgaben
Masse und Gewichtskraft 1
1.
Auf der Erde dehnen zwei Körper dieselbe Schraubenfeder im Verhältnis 1:2.
Wie dehnen sie diese Schraubenfeder
a) auf dem Mars,
b) in einer Raumkapsel (antriebslos),
c) in einer Raumkapsel während des Starts ?
2.
Kann man Gewichtskräfte mit der Balkenwaage vergleichen ? Kann man sie damit
auch messen, wenn man nicht weiß, wo man sich befindet ?
3.
Der Kaufmann wiegt 100 g Erbsen mit der Balkenwaage ab.
Müsste er am Nordpol weniger Erbsen auf die Waage legen ?
4.
Um wieviel verlängert sich eine Feder (Federkonstante D = 3 N/cm), wenn man sie
auf dem Mond mit einem Körper der Masse m = 5 kg belastet ?
5.
Welche Masse muss ein Körper haben, damit der Unterschied seiner Gewichtskräfte
an Pol und Äquator 1,0 N beträgt ?
6.
Zwischen der Masse m und der Gewichtskraft FG eines Körpers besteht der Zusammenhang FG = m⋅g. An der Erdoberfläche ist g0 = 9,81 N/kg. In 10 km Höhe ist
g1 = 9,50 N/kg.
Welche Gewichtskraft erfährt ein wissenschaftlicher Ballon in der Höhe 10 km, der am
Erdboden die Gewichtskraft 1 240 N besitzt ?
7.
Ein wissenschaftliches Gerät mit der Masse m = 12,6 kg wird auf dem Planeten Mars
abgesetzt. Die Gewichtskraft des Gerätes auf dem Mars ist FG = 47,4 N.
Welcher Wert für g ergibt sich hieraus für die Marsoberfläche ?
8.
Astronauten bestimmen die Gewichtskraft eines Körpers der Masse 10 kg zu 38 N.
Welche Messgeräte benutzen sie ? Berechne den Ortsfaktor !
Auf welchem Planeten könnten sie sein ?
9.
Können wir Massen auch mit Hilfe der Verlängerung von Federn vergleichen ?
Warum schreibt man auf die Skala nicht die Einheit kg ?
Masse_01A **** Lösungen 2 Seiten
1 (1)
www.mathe-physik-aufgaben.de
Übungsaufgaben
Masse und Gewichtskraft 2
1.
Zwei Quader Q1 und Q2 haben die gleiche Masse.
a) Unter welcher Voraussetzung haben die beiden Quader auch die gleiche
Gewichtskraft ?
b) Nenne Beispiele für den Fall, dass die Quader nicht die gleiche Gewichtskraft
aufweisen.
2.
Ein Astronaut im Astronautenanzug hat auf der Erde die Gewichtskraft FG,E = 980 N.
a) Berechne die Masse m des Astronauten ! (Ortsfaktor: gErde = 9,81N / k g)
b) Welche Masse hat der gleiche Astronaut auf dem Mond ?
c) Welche Gewichtskraft FG,M hat der Astronaut auf dem Mond ?
(Ortsfaktor: gMond = 1,6 N / k g)
3.
Ein Schraubwerkzeug für Astronauten auf der Mondoberfläche hat die Masse
m1 = 22 kg.
Welche Masse m2 müsste ein Übungswerkzeug auf der Erde haben, damit die
Astronautenanwärter bei Übungen auf der Erde mit der gleichen WerkzeugGewichtskraft FG,E belastet werden ?
(Ortsfaktor auf dem Mond gM = 1,62 N / k g, auf der Erde gE = 9,81N / k g)
4.
Jupiter ist der größte Planet im Sonnensystem. Eine Raumsonde würde in der Nähe
seiner (nicht festen) Oberfläche etwa 2,5 mal so stark angezogen werden wie auf der
Erdoberfläche. (Ortsfaktor Erdoberfläche gE = 9,81 N / k g)
a) Berechne den Ortsfaktor gJ der Jupiteroberfläche !
b) Eine Raumsonde hat die Masse m = 1250 kg.
Berechne die Anziehungskraft FG,J, die der Jupiter auf die Raumsonde in der
Nähe der Jupiteroberfläche ausübt !
5.
Für eine Forschungsstation auf dem Südpol der Erde (Ortsfaktor: gS = 9,83 N / k g) wird
in Nürnberg (Ortsfaktor: gN = 9,81 N / k g) ein Fahrzeug gebaut. Die Masse des
Fahrzeugs ist m = 10 600 kg.
Berechne die Gewichtskraftzunahme, die sich ergibt, wenn das Fahrzeug beim
Transport von Nürnberg zum Südpol transportiert wird !
6.
Am Äquator der Erde ist der Ortsfaktor gÄ = 9,78 N / k g, am Nordpol gN = 9,83 N / k g.
Ein Stein unbekannter Masse wird vom Äquator zum Nordpol transportiert.
Berechne, um wieviel Prozent der Stein am Nordpol schwerer ist als am Äquator !
Masse_02A **** Lösungen 3 Seiten
1 (1)
www.mathe-physik-aufgaben.de
Gymnasium
Schiefe Ebene / Energieerhaltung
Klasse 7
GP_A0346 Nr. 1:
1.
Eine Glaskugel der Masse 50 g
rollt eine schräg liegende Rinne
der Länge 0,8 m hinab.
Fallbeschleunigung in dieser
m
Aufgabe: g  10 2 .
s
a) Bestimme mit Hilfe einer
Kräftezerlegung die Hangabtriebskraft FH .
Kräftemaßstab: 1N 10 cm
b) Wie groß ist die Beschleunigung der Kugel in der Rinne ?
GP_A0346 Nr. 2:
2.
Ein 400 kg schwerer Wagen einer
Achterbahn startet aus einer Höhe
von h  28 m und fährt in einen
kreisförmigen Looping mit 5 m
Radius ein.
Wie hoch ist die Geschwindigkeit
des Wagens im höchsten Punkt
des Loopings ?
Reibungseffekte bleiben
unberücksichtigt.
GP_A0349 Nr. 2:
3.
Am Start eines Seifenkistenrennens steht das neue Seifenkisterl (FG = 140 N) von
Sebastian. Die Startrampe hat einen Neigungswinkel von 20°.
Ermittle zeichnerisch die Größe der Hangabtriebskraft die auf das Seifenkisterl wirkt.
Runde auf ganze Newton.
Wähle als Maßstab: 10 N 0,5 cm
Schi-Ebene_01A **** Lösungen 3 Seiten (Schi-Ebene_01L)
1 (2)
© www.mathe-physik-aufgaben.de
Gymnasium
Schiefe Ebene / Energieerhaltung
Klasse 7
GP_A0351 Nr. 1:
4.
Sandra lässt einen Wagen eine schiefe Ebene hinab rollen und möchte damit die
Größe der Kraft bestimmen die den Wagen hinunter zieht (Ein Kraftmesser steht
nicht zur Verfügung).
a) Welche zwei
Größen muß Sandra
kennen wenn sie die
Kraft berechnen will,
die den Wagen nach
unten beschleunigt ?
b) Welche Messungen muss Sandra machen, wenn sie wissen will mit welcher
Geschwindigkeit der Wagen im Punkt B ankommt ?
c) Welche Größen muss Sandra außerdem noch messen ?
d) Wähle nun selbst (sinnvolle) Werte die Sandra gemessen haben könnte und
ergänze damit die Skizze.
Berechne mit diesen Werten die Kraft, die den Wagen nach unten beschleunigt.
Schi-Ebene_01A **** Lösungen 3 Seiten (Schi-Ebene_01L)
2 (2)
© www.mathe-physik-aufgaben.de
Gymnasium
Schiefe Ebene / Energieerhaltung
Klasse 8
GP_A0093 Nr. 5:
1.
Eine Stahlkugel der Masse 2,5 kg wird in der gezeichneten Lage von einem ortsfesten
Elektromagneten gehalten. Der Strom wird nun abgeschaltet und die Kugel rollt den
Abhang hinunter. Alle Reibungseffekte sollen so gering sein, dass sie im Folgenden
vernachlässigt werden dürfen.
a) Berechne die Geschwindigkeit v1 , mit welcher die Kugel an der tiefsten Stelle der
Bahn ankommt.
b) Bestimme die Geschwindigkeit v 2 , der Kugel in der Höhe h2 .
GP_A0094 Nr. 3:
2.
Ein Wagen mit der Gewichtskraft 500 N soll 3,5 m hochgehoben werden.
a) Wie groß ist die dafür aufzubringende Hubarbeit ?
b) Man kann den Wagen auch über die gezeichnete schiefe Ebene der Länge 8 m
hochziehen. (Das Bild ist nicht maßstäblich !)
Die Reibung darf vernachlässigt werden.
Wie groß ist die dafür benötigte Zugkraft ? Begründe deine Antwort mit der
„goldenen Regel der Mechanik“.
Schi-Ebene_02A **** Lösungen 11 Seiten (Schi-Ebene_02L)
1 (6)
© www.mathe-physik-aufgaben.de
Gymnasium
Schiefe Ebene / Energieerhaltung
Klasse 8
GP_A0098 Nr. 4:
3.
Beachte: Bei den Aufgabenteilen a), b) und c) wird die Reibung vernachlässigt.
Ein Spielzeugauto durchläuft die skizzierte Bahn von S über A und B nach C der
Spielzeug-Achterbahn.
Dabei wird es vom Startpunkt S zunächst mit einem Federkatapult zum Punkt A
katapultiert, so dass der Wagen im Punkt A für einen Moment die Geschwindigkeit
null besitzt.
a) Nenne die zwischen S über A und B nach C auftretenden Energieformen und gib
an, in welchen Punkten die genannten Energien jeweils maximal bzw. minimal sind.
b) Ein zweites Auto mit vierfacher Masse des ersten Autos wird nun ebenfalls zum
Punkt A katapultiert. Wiederum gerade so, dass die Geschwindigkeit im Punkt A
Null ist.
Wie ändert sich die Geschwindigkeit dieses zweiten Autos im Punkt B (verglichen
mit der Geschwindigkeit des ersten Autos in B) ? Begründe !
c) Die Schraubenfeder des Federkatapults besitzt die Federhärte D  650 N .
m
Wie weit muss die Feder mindestens zusammengedrückt werden, damit ein
Spielzeugauto der Masse 150 g zum Punkt A katapultiert wird ?
d) In Wirklichkeit stellt man fest, dass der Wagen auf seiner Fahrt Energie „verliert“.
Warum ist dies kein Widerspruch zu der Tatsache, dass Energie eine
Erhaltungsgröße ist ?
GP_A0100 Nr. 2:
4.
Erkläre ausreichend genau die physikalische Aussage, die mit der
„Goldenen Regel der Mechanik“ ausgedrückt werden soll.
Die Erklärung soll mit Hilfe der Graphik zu dieser Aufgabe durchgeführt werden !
Schi-Ebene_02A **** Lösungen 11 Seiten (Schi-Ebene_02L)
2 (6)
© www.mathe-physik-aufgaben.de
Gymnasium
Schiefe Ebene / Energieerhaltung
Klasse 8
GP_A0101 Nr. 2:
5.
Eine Stahlkugel lässt man aus einer
Höhe h reibungsfrei hinabrollen.
Unten stößt die Kugel gegen einen
Holzklotz.
Daraufhin kann der Holzklotz einen
bestimmten Weg s bis zum
Stillstand zurücklegen.
a) Gib die auftretenden Energieumwandlungen an.
b) Von welcher Höhe muss die Kugel der Masse 200 g losgelassen werden, damit sie
beim Aufprall auf den Holzklotz die Geschwindigkeit 3,6 m/s besitzt ?
c) Der zu Beginn beschriebene Vorgang erfährt jetzt eine Veränderung:
Der Holzklotz soll reibungsfrei (z. B. auf idealem Glatteis) die Wegstrecke x
zurücklegen und am Ende der Wegstrecke auf eine entspannte Feder treffen. Dabei
kann der Holzklotz die Feder um die Strecke s zusammenstauchen.
Begründe, ob folgende Aussagen zutreffen:
I)
„Die Spannenergie der gestauchten Feder ist zur Anfangshöhe h der Kugel
direkt proportional.“
II) „Die Masse m der Kugel ist zur Federstauchung s direkt proportional.“
GP_A0102 Nr. 1:
6.
Ein 60 g schweres Spielzeugauto soll wie in der Skizze mit Hilfe eines „Federkatapults“
(zusammengedrückte Feder) waagerecht abgeschossen werden und dann über einen
Hügel fahren. Bei den nun folgenden Überlegungen und Berechnungen kann man alle
auftretenden Reibungskräfte vernachlässigen !
a) Welche Spannenergie steckt in der Feder, wenn diese die Federhärte D = 7,5 N/cm
besitzt und um 2,8 cm zusammengedrückt wurde ?
b) Wie schnell fährt das Auto am Punkt T, nachdem es die Feder verlassen hat ?
c) Schafft es das Auto über den 40 cm hohen Hügel zu fahren ? (Rechnung !)
d) Wenn ja, wie schnell ist dann das Fahrzeug im Punkt U nach dem Hügel ?
(Begründung !)
Schi-Ebene_02A **** Lösungen 11 Seiten (Schi-Ebene_02L)
3 (6)
© www.mathe-physik-aufgaben.de
Gymnasium
Schiefe Ebene / Energieerhaltung
Klasse 8
GP_A0103 Nr. 2:
7.
Eine Kugel wird im höchsten Punkt der folgenden Kugelbahn losgelassen. Mit welcher
Geschwindigkeit kommt die Kugel am Ende der Kugelbahn an ?
Reibung wird hier vernachlässigt.
GP_A0111 Nr. 3:
8.
Auf dem Oktoberfest ist ein h 1  18 m hoher „Dreierlooping“ aufgebaut.
Die Wagen werden zu Beginn der Fahrt auf eine Höhe h2  28 m gezogen und fahren
anschließend in den „ersten“ Looping ein (Die antriebslosen Wagen starten oben
mit v = 0 m/s).
a) Bestimme die Geschwindigkeit der Wagen im
tiefsten Punkt des ersten Loopings (ohne Reibung) !
b) Bestimme die Geschwindigkeit der Wagen im
höchsten Punkt des ersten Loopings (ohne Reibung).
c) Die letzte Loopingschleife ist
wesentlich kleiner als die erste.
Welcher physikalische Grund
verbirgt sich dahinter ?
Erkläre kurz !
GP_A0114 Nr. 3
9.
Ein Spielzeugauto ( m  120 g ) wird durch eine gespannte Feder der Federhärte
D  48 N / cm auf ebener Bahn beschleunigt. Die Feder wurde um s  2,6 cm
zusammengedrückt und dann schlagartig entspannt. Reibung wird nicht berücksichtigt.
a) Welche Energie hatte das Auto beim Start?
b) Kurz nach dem Start durchfährt das Spielzeugauto einen Looping. Damit es sicher
durch die Loopingschleife kommt, soll die Geschwindigkeit im höchsten Punkt
3,6 m / s betragen. Welchen Durchmesser hat der Looping?
Schi-Ebene_02A **** Lösungen 11 Seiten (Schi-Ebene_02L)
4 (6)
© www.mathe-physik-aufgaben.de
Gymnasium
Schiefe Ebene / Energieerhaltung
Klasse 8
GP_A0078 Nr. 1
10.
Bei einer Achterbahn wird der Zug in dem die Fahrgäste sitzen, auf eine Starthöhe
von 40,0 m hochgezogen.
a) Berechne die maximale Geschwindigkeit
in km / h , die der Zug erreichen könnte,
wenn die Reibung nicht berücksichtigt wird.
Spielt dabei die Anzahl der Fahrgäste
eine Rolle? (Begründung!)
b) Aufgrund von Reibungseffekten beträgt
die Geschwindigkeit (im Punkt B)
„nur“ 26 m / s .
Berechne den Energieverlust in Prozent !
c) Gleich im Anschluss an die erste tiefste
Stelle folgt ein großer Looping mit einer Gesamthöhe von 20 m. Nach TÜVVorgaben muss die Geschwindigkeit des Zuges an seiner höchsten Stelle
mindestens 10 m / s betragen, sonst würde der Zug abstürzen.
Ist diese Bedingung bei Berücksichtigung der Reibung erfüllt ?
Begründung durch Rechnung !
GP_A0084 Nr. 1
11.
Eine Kugel rollt auf der skizzierten Bahn vom
Punkt A  hA  27 m  hinunter zu B, dann
durch das Looping über C und B und trifft
im Punkt D auf eine Feder der Härte
12 N / cm , die bis zum Punkt E
zusammengedrückt wird.
Hinweis: Reibung wird bei
diesen Aufgaben nicht
berücksichtigt.
a) Wie groß ist die Geschwindigkeit in m/s der Kugel im Punkt B?
b) Berechne hC , wenn die Kugel im Punkt C die Geschwindigkeit 47 km/h hat.
c) Wie groß ist die Masse der Kugel, wenn die Feder um  s  13 cm
zusammengedrückt wird?
Schi-Ebene_02A **** Lösungen 11 Seiten (Schi-Ebene_02L)
5 (6)
© www.mathe-physik-aufgaben.de
Gymnasium
Schiefe Ebene / Energieerhaltung
Klasse 8
GP_A0110 Nr. 3
12.
Die Feder D  260 N / m  in nachfolgender Abbildung ist in Punkt (1) um 6,5 cm
zusammengedrückt. Vor ihr ruht in einer Bahn ein Spielzeugauto  m  165 g  . Die
Feder wird nun entspannt und katapultiert das Auto bis zu Punkt (4) hinauf, wo es zum
Stehen kommt. (Reibungskräfte sind zu vernachlässigen.)
a) Berechne die in der Feder gespeicherte Energie!
b) Gib an, welche Energieformen in den Punkten (2), (3) und (4) jeweils auftreten !
(Fachbegriffe ausschreiben!)
c) Nach dem Versuch wird das Spielzeugauto aufgeräumt. Es wird in Punkt (4) hochgehoben und in ein Regal gelegt. Dort besitzt das Auto eine Energie von 2,1 J.
Berechne die erforderliche Arbeit, um das Auto von Punkt (4) ins Regal zu legen!
Schi-Ebene_02A **** Lösungen 11 Seiten (Schi-Ebene_02L)
6 (6)
© www.mathe-physik-aufgaben.de
Gymnasium
Schiefe Ebene / Energieerhaltung
Klasse 9
GP_A0203 Nr. 5:
1.
Ein Wagen auf einer schiefen
Ebene wird durch eine Schnur
am hinunterrollen gehindert.
DieGewichtskraft des Wagens
ist FG .
Die Kraft F1 wirkt auf den Wagen,
die Kraft F2 wirkt auf die Befestigung.
a) Zerlege FG so, daß man die
Hangabtriebskraft FH erhält.
b) Zeichne alle Kräfte ein, die
noch auf den Wagen wirken.
c) Welche der Kräfte sind im Kräftegleichgewicht und welche der Kräfte sind
Wechselwirkungskräfte ?
GP_A0204 Nr. 5:
2.
In einem Versuch wird ein Laborwagen
( m 1 = 500 g ) der über eine Rolle,
mit dem Gewicht der Masse m 2 = 200 g
verbunden ist, beschleunigt, indem das
Gewicht m 2 frei fallen gelassen wird. Seil und Rolle werden als
masselos angenommen. Reibung bleibt unberücksichtigt.
a) Berechne die beschleunigende
Kraft FB .
b) Berechne die Beschleunigung a.
GP_A0206 Nr. 2:
3.
In einem Versuch rollt eine Kugel mit der
Anfangsgeschwindigkeit v 0 = 3 m / s eine
schiefe Ebene hinauf. Nach 1,2 s kommt
die Kugel für einen Moment zum Stillstand.
a) Berechne wie hoch (Höhe h) die
Kugel bis zu ihrem Stillstand
gerollt ist.
b) Bestimme die Bremsbeschleunigung
die auf die Kugel wirkt.
c) Berechne den Weg s den die Kugel auf der schiefen Ebene zurücklegt.
Schi-Ebene_03A **** Lösungen 4 Seiten (Schi-Ebene_03L)
1 (2)
© www.mathe-physik-aufgaben.de
Gymnasium
Schiefe Ebene / Energieerhaltung
Klasse 9
GP_A0207 Nr. 5:
4.
Ein Rodler (m = 65 kg, einschließlich Schlitten) auf einer Sommerrodelbahn fährt mit
v = 0 m/s beginnend die Bahn hinab. Während den ersten 30 m verläuft die Bahn
gerade und mit einem Neigungswinkel von 25° gegen d ie Horizontale. Als konstante
Reibungskraft soll 120 N angenommen werden.
a) Fertige eine vereinfachte Skizze an, in der alle auftretenden Kräfte mit maßstabsgerechten Kraftpfeilen eingezeichnet sind.
b) Bestimme durch Messen (Skizze) und Rechnen die Beschleunigung des Rodlers.
[Ergebnis: a = 2,4 m / s2 ]
c) Wie lange dauert die Fahrt auf den ersten 30 m der Bahn ?
Welche Geschwindigkeit hat der Rodler nach diesen 30 m erreicht ?
GP_A0210 Nr. 4:
5.
Eine Kugel rollt zum Zeitpunkt t = 0 mit einer Anfangsgeschwindigkeit von 5,2 m ⋅ s − 1
eine schiefe Ebene hinauf, auf der sie die Beschleunigung − 4,0 m ⋅ s − 2 erfährt.
a) Nach welcher Zeit kommt die Kugel zum Stillstand ?
b) Nach welcher Zeit passiert die Kugel wieder ihren Ausgangspunkt (am Beginn
der schiefen Ebene) ?
Schi-Ebene_03A **** Lösungen 4 Seiten (Schi-Ebene_03L)
2 (2)
© www.mathe-physik-aufgaben.de
Gymnasium
Schiefe Ebene / Energieerhaltung
Klasse 10 / 11
1.
Ein Körper der Masse m bewegt sich antriebslos eine schiefe Ebene (Neigungswinkel α)
hinab. Berechne die Beschleunigung des Körpers, wenn die Reibungszahl zwischen
Körper und Bahn µ ist.
2.
Auf einer schiefen Ebene liegt ein quaderförmiger Körper. Langsam wird die Ebene
stärker geneigt und bei einem Neigungswinkel von 28° beginnt der Körper zu rutschen.
Wie groß ist die Haft - Reibungszahl µ ?
3.
Ein Transportschlitten der Masse 8 kg soll aus der Ruhe mit konstanter Beschleunigung
in 5 s eine schiefe Ebene ( α = 20° ) von 50 m Länge hochgezogen werden.
Die Reibungszahl während der Bewegung ist 0,12.
a) Erstelle eine Skizze und zeichne die auftretenden Kräfte ein.
b) Welche Zugkraft ist für den Wagen erforderlich ?
4.
Ein Körper (m = 20 kg) bewegt sich auf einer schiefen Ebene (Neigungswinkel 15°).
Der Reibungskoeffizient zwischen Körper und Bahn ist 0,2.
a) Welche Geschwindigkeit hat der Körper nach 6 m, wenn er sich aus der Ruhe
hangabwärts bewegt ?
b) Mit welcher Kraft muss man den Körper auf der schiefen Ebene nach oben ziehen,
damit seine Beschleunigung 2 m / s2 beträgt ?
5.
Ein Motorrad (m = 280 kg) steht am Anfang einer Straße, die eine Steigung von 18%
aufweist. Bei einer konstanten Beschleunigung hangaufwärts soll nach 150 m die
Geschwindigkeit 30 m/s erreicht werden.
a) Welche konstante Beschleunigung ist dazu erforderlich ?
b) Wie groß ist Antriebskraft am Hinterrad, wenn die Reibungszahl 0,12 beträgt ?
6.
Ein Körper fällt mit der Anfangsgeschwindigkeit v = 0 frei aus der Höhe h senkrecht
nach unten.
Zeige, dass der Körper die gleiche Geschwindigkeit
erreicht, als wenn er sich aus der Höhe h eine
schiefe Ebene hinunterbewegt.
(Reibungseffekte bleiben unberücksichtigt).
Schi-Ebene_04A **** Lösungen 22 Seiten (Schi-Ebene_04L)
1 (5)
© www.mathe-physik-aufgaben.de
Gymnasium
Schiefe Ebene / Energieerhaltung
Klasse 10 / 11
7.
Die Masse m kann auf einer schiefen Ebene gleiten,
während Masse M über einen dünnen Faden
und eine kleine Rolle mit Masse m verbunden ist.
Fadenmasse und Reibungseffekte
bleiben unberücksichtigt.
Im Ausgangszustand ist diese
Anordnung in Ruhe weil M in der
Höhe h festgehalten wird.
a) Es sei m = 4,0 kg und M = 2,0 kg
Wie groß muss α sein, damit sich die Anordnung nicht in Bewegung setzt, wenn
man M loslässt ?
b) Nun sei α = 15° und h = 1,5 m .
Wie lange dauert es nach dem Loslassen, bis M die Höhe h zurückgelegt hat ?
Mit welcher Geschwindigkeit setzt M auf dem Boden auf ?
8.
Auf eine Masse m, die sich auf einer schiefen Ebene befindet,
wirkt über eine Rolle die Masse M ein (siehe Skizze).
Seil und Rolle sind als masselos zu betrachten.
Gegeben sind:
m = 3,0 kg; h = 1,0 m; α = 30°
Haftreibungszahl µH = 0,70
Gleitreibungszahl µG = 0,30
a) Gib die Grenzmasse für M an, so dass
sich das Gespann nicht nach rechts
in Bewegung setzt !
Ab hier gelte: M = 5,0 kg !
b) Das Gespann wird aus obiger Stellung losgelassen.
Nach welcher Zeit trifft M am Boden auf ?
c) Welche Geschwindigkeit hat m zu diesem Zeitpunkt ?
d) Was passiert mit m nach dem Aufsetzen von M ?
e) Würde m (ohne an M angehängt zu sein) vom Ruhezustand aus auf der schiefen
Ebene liegen bleiben oder zurück rutschen ?
Schi-Ebene_04A **** Lösungen 22 Seiten (Schi-Ebene_04L)
2 (5)
© www.mathe-physik-aufgaben.de
Gymnasium
Schiefe Ebene / Energieerhaltung
Klasse 10 / 11
9.
Die Masse m wird auf einer schiefen Ebene
durch die Masse M reibungsfrei nach oben
gezogen. Masse m startet aus der Ruhe im
Punkt A. Nachdem sie den Weg x = AB
zurückgelegt hat, reißt der Verbindungsfaden zwischen M und m.
(Die Massen von Faden und Rolle
bleiben unberücksichtigt)
Rechne mit Hilfe von Energiebilanzen.
a) Stelle eine Gleichung auf für die Geschwindigkeit
von m im Punkt B.
b) Wie groß ist bei der Masse m durch diese Bewegung die Zunahme an Energie ?
c) Wie weit bewegt sich m (nach der Trennung von M) noch über den Punkt B
der schiefen Ebene hinaus (allgemeine Lösung, ohne Zahlenwerte) ?
d) M fällt nach der Trennung von m noch 25 cm weiter, und schlägt dann auf dem
Boden auf. Wie hoch ist die Auftreffgeschwindigkeit, für
M = 5 kg, m = 3 kg, x = 3 m, α = 30°
GP_A0005 Nr. 3:
10.
Schiefe Ebene
a) Beschreibe allgemein, welche Berechnungsschritte notwendig sind, um zu entscheiden,
ob sich das skizzierte Gespann aus dem
Stillstand heraus in Bewegung setzt. (Keine
Berechnung, nur eine Beschreibung, wobei
zur Unterscheidung die Indizes 1 und 2 zu
verwenden sind !)
b) Die Bedingungen seien nun so, dass sich das Gespann nach rechts in Bewegung
setzt. Berechne die Beschleunigung, die das Gespann dabei erfährt.
Werte: α = 20°, β = 50°, m 1 = 1,2 kg, m2 = 5,6 kg, µ g1 = 0,20 , µ g2 = 0,30 .
11.
Ein Spielzeugauto (m = 300 g) soll eine Kreisbahn
mit r = 0,35 m durchfahren.
Das Auto hat an der Stelle A eine Geschwindigkeit
von v A = 5 m / s .
Reibungseffekte bleiben unberücksichtigt.
a) Mit welcher Geschwindigkeit
durchfährt das Spielzeugauto
die höchste Stelle B der Kreisbahn ?
b) Mit welchem Teil seiner Gewichtskraft FG wird das Auto im Punkt B gegen die Bahn
gepresst ?
Schi-Ebene_04A **** Lösungen 22 Seiten (Schi-Ebene_04L)
3 (5)
© www.mathe-physik-aufgaben.de
Gymnasium
Schiefe Ebene / Energieerhaltung
Klasse 10 / 11
12.
Eine Stahlkugel (m = 200 g) soll eine Kreisbahn
mit r = 25 cm durchlaufen.
Welche Mindest-Geschwindigkeit v A im Punkt A
ist notwendig, damit die Kugel im Looping
(im Punkt B) nicht herab fällt ?
Reibungseffekte bleiben unberücksichtigt.
13.
Ein Achterbahnwagen (m W = 220 kg)
mit einem Fahrgast (m G = 70 kg) startet
im Punkt A (h = 15 m) mit v 0 = 0 m / s
(antriebslos) und fährt dann durch einen
Looping mit Radius r = 4 m .
Reibungseffekte bleiben unberücksichtigt.
Wagen und Fahrgast sind als Massepunkte
zu betrachten.
a) Welche Geschwindigkeit hat der
Wagen (mit Fahrgast) in B ?
b) Mit welcher Geschwindigkeit passiert der Wagen die höchste Stelle C der
Kreisbahn ?
c) Berechnen Sie die Anpresskraft des Wagens auf die Bahn im höchsten Punkt C.
Erstellen Sie ein beschriftetes Kräftediagramm mit den wirkenden Kräften.
d) Mit welcher Beschleunigungskraft wird der Fahrgast im Punkt C in seinen Sitz
gedrückt ? Wie hoch ist dort die Beschleunigung ?
e) Wie hoch ist die Beschleunigung auf den Fahrgast im tiefsten Punkt B der Bahn ?
14.
Ein antriebsloses Spielzeugauto fährt mit
der Geschwindigkeit v A = 2,0 m / s beim
Punkt A in eine Schleifenbahn ein. Der Punkt B
liegt 1,4 m tiefer. Reibungseffekte bleiben
unberücksichtigt.
a) Welche Geschwindigkeit hat das Auto in B ?
b) Welchen Radius hat der Looping, wenn die
Bahn in B eine Belastung erfährt, die der
6-fachen Gewichtskraft des Autos entspricht ?
c) Nun soll die Bahn im Punkt C enden, so dass
das Auto dort die Bahn verlässt.
In welche Richtung fliegt es weiter, welche Höhe erreicht es und mit welcher
Geschwindigkeit schlägt es nach dem Flug auf dem Boden auf ?
Schi-Ebene_04A **** Lösungen 22 Seiten (Schi-Ebene_04L)
4 (5)
© www.mathe-physik-aufgaben.de
Gymnasium
Schiefe Ebene / Energieerhaltung
Klasse 10 / 11
15.
Ein Spielzeugauto ( m = 180 g ) durchfährt eine vertikale Kreisbahn ( r = 30 cm ).
Reibungseffekte sollen unberücksichtigt bleiben.
a) Welche Geschwindigkeit muss das
Spielzeugauto in D besitzen, wenn
an dieser Stelle der Betrag der
Gewichtskraft des Autos halb so groß
ist wie der Betrag der Kraft auf die
Unterlage ?
b) Wie hoch muss in diesem Fall der
Startpunkt A liegen ?
c) Berechnen Sie den Betrag der
Zentrifugalkraft im Punkt C.
c) Wie hoch ist die Geschwindigkeit des
Spielzeugautos in B ?
GP_A0003 Nr.1:
16.
Eine Bobbahn habe idealisiert das folgende Streckenprofil:
Auf der waagrechten Anschubstrecke s = 25 m wird der ruhende Bob der Masse
mBob = 220 kg von zwei Sportlern mit konstanter Kraft F1 = F2 auf v = 10 m / s
angeschoben. Der Reibungskoeffizient zwischen Kufen und Eis betrage µ = 0,02 . Nach
der Anschubphase springen die beiden Sportler im Punkt A in den Bob und beginnen
ihre l = 1200 m lange Fahrt ins Ziel. Die beiden Bobfahrer haben zusammen eine
Masse von 160 kg. Der Höhenunterschied ist h = 82 m . Die Zeitmessung beginnt im
Punkt A und endet im Ziel Z.
a) Welchen Neigungswinkel ϕ hat die Bobbahn?
b) Berechnen Sie die Beschleunigung in der Anschubphase. Wie lange dauert sie?
c) Berechnen Sie F1 und F2 .
d) Welche Beschleunigung a* hat der Bob auf der Fahrt bergab?
e) Welche Fahrzeit für die 1200 m erreicht der Bob und mit welcher Geschwindigkeit
v Ziel überquert der Bob die Ziellinie Z?
f)
Welche konstante Bremskraft muss aufgebracht werden, wenn der Bob nach dem
Ziel auf einer Länge von b = 110 m zum Stehen gebracht wird?
Berechnen Sie die erforderliche Bremszeit t Brems .
g) Erstellen Sie je ein qualitatives v - t - Diagramm und ein a - t - Diagramm des
gesamten Vorgangs vom Beginn des Anschiebens bis zum Stillstand 110 m nach
dem Ziel.
Kennzeichnen Sie in den Diagrammen die drei Teilstrecken s, l und b.
Schi-Ebene_04A **** Lösungen 22 Seiten (Schi-Ebene_04L)
5 (5)
© www.mathe-physik-aufgaben.de
Technikerschule / Fachhochschule
Technische Mechanik
Statik – Zentrale Kräftesysteme
1.
Auf das Fundament der Verankerung eines
abgespannten Mastes wirken zwei Seilkräfte
F1 = 300 N und F2 = 180 N unter den Winkeln
α = 45° und β = 30° zur Horizontalen.
a) Wie groß ist die resultierende Kraft auf das
Fundament ?
(Zeichnerische und analytische Lösung)
b) Welcher Winkel zur Horizontalen stellt sich ein ?
2.
An einem Block greifen die beiden Kräfte
F1 = 200 N und F2 = 120 N unter den
angegebenen Winkeln an.
a) Bestimmen Sie grafisch, grafoanalytisch
(mit Hilfe trigonometrischer Beziehungen)
und analytisch mit Vektoraddition die
Resultierende (Betrag und Richtung).
b) Welche Größe muss die Kraft F2 haben,
damit die vertikale Komponente der
Resultierenden verschwindet? (Richtung bleibt gleich)
c) Wie groß muss der Winkel zwischen F2 (120 N) und der Horizontalen werden,
damit bei gleichem Betrag von F2 die Resultierende nur eine horizontale
Komponente hat ?
3.
Ein Baum soll von vier Holzfällern umgelegt werden.
Welche Wirkung wird hervorgerufen, wenn jeder
der Holzfäller nach nebenstehendem Schema
mit einer Kraft von F = 600 N zieht ?
Berechnen Sie mit der analytischen Methode
und kontrollieren Sie mittels Kräfteparallelogramm.
Statik_01A **** Lösungen 12 Seiten (Statik_01L)
1 (4)
www.mathe-physik-aufgaben.de
Technikerschule / Fachhochschule
Technische Mechanik
Statik – Zentrale Kräftesysteme
4.
Ein Schiff soll von zwei Schleppern in
x - Richtung gezogen werden.
Die Seilkräfte betragen F1 = 3 kN und
F2 = 2 kN . Der Winkel zwischen den
Seilen beträgt 60°.
Unter welchem Winkel α zur Fahrtrichtung x muss F1 angreifen ?
Wie groß ist die Resultierende ?
5.
An einem Mast greifen zwei Seile unter den
gegebenen Winkeln an. Die Seilkräfte betragen
F1 = 4 kN und F2 = 2 kN .
a) Zu bestimmen ist die resultierende Kraft
(Betrag und Richtung).
b) Wie muss der Kraftvektor F1 beschaffen sein –
Betrag oder Wirkungslinie von Frage a) –
damit die Wirkungslinie der Resultierenden
in der Mastachse liegt ?
6.
Ein mit 4600 N belastetes Seil ist über eine Seilrolle
geführt, so dass das freie Seilende unter 60° Neigung
gegen die Senkrechte von der Rolle abläuft.
Die Rolle ist an einer beweglich gelagerten Stange
aufgehängt.
a) Unter welchem Winkel α gegen die
Senkrechte stellt sich die Pendelstütze ein ?
b) Wie groß ist der Betrag der Resultierenden ?
7.
An einer verschieblich gelagerten Buchse greift
eine Zugfeder in der gezeigten Weise an.
Die Länge der unbelasteten Feder ist I0 = 35 cm ,
ihre Federsteifigkeit c = 25 N / cm .
a) Berechnen Sie die Federkraft.
b) Bestimmen Sie die Tangential- und
Normalkomponenten der Federkraft.
Statik_01A **** Lösungen 12 Seiten (Statik_01L)
2 (4)
www.mathe-physik-aufgaben.de
Technikerschule / Fachhochschule
Technische Mechanik
Statik – Zentrale Kräftesysteme
8.
Ein Schlitten soll mit einer Kraft von
insgesamt 600 N in Richtung x gezogen werden.
Die zwei Zugseile greifen unter 30° und 15° zur
x - Richtung an.
Wie groß müssen die beiden Seilkräfte sein ?
9.
Für die dargestellte Kniehebelpresse bestimme man den Betrag, der am Gelenk B
wirkenden Kraft F, die eine Presskraft von FQ = 12 kN hervorruft.
Welcher Verstärkungsfaktor liegt vor ?
10.
An den 3 Seilen der dargestellten
Anordnung hängt jeweils ein Gewicht
(unterschiedliche Massen).
Die Rollen sind reibungsfrei.
a) Welche Winkel α und β
stellen sich ein ?
b) Welche Bedingungen
müssen für die Gewichte
gelten, damit sich eine
sinnvolle Lösung ergibt ?
11.
Zwei Zylinder werden nach nebenstehender Skizze gelagert.
Zyl.-Durchmesser: d1 = 50 mm, d2 = 30 mm ;
Gewichtskräfte: FG1 = 8 N, FG2 = 3 N
Winkel: α = 45°, β = 30°
a) Bestimmen Sie die Auflagerkräfte in den
Punkten A, B, C und die Kontaktkraft im Punkt D.
b) Wie groß müsste die Gewichtskraft FG2
mindestens sein, damit Zylinder 1
angehoben wird ?
(ohne Reibung und bei unveränderten Geometrien)
Statik_01A **** Lösungen 12 Seiten (Statik_01L)
3 (4)
www.mathe-physik-aufgaben.de
Technikerschule / Fachhochschule
Technische Mechanik
Statik – Zentrale Kräftesysteme
12.
Auf einen auf einer schiefen Ebene liegenden Block
(Gewichtskraft FG = 400 N ) greift die
Stangenkraft FS = 300 N an.
a) Wie groß ist die Resultierende ?
b) Bestimme Tangential- und Normalkomponente
(zur schiefen Ebene) der Resultierenden.
13.
Die Abbildung zeigt ein Knotenblech, das durch die Stäbe 1 bis 6 im Gleichgewicht
gehalten wird. Welche Kräfte F4 und F6 müssen im Gleichgewichtsfall wirken ?
Statik_01A **** Lösungen 12 Seiten (Statik_01L)
4 (4)
www.mathe-physik-aufgaben.de
Realschule / Gymnasium / Berufliche Schulen
Bewegungsaufgaben
1.
Zwei Lastwagen fahren von den Orten A und B mit der Entfernung 140 km einander
entgegen, der eine mit der Geschwindigkeit 60 km/h, der andere mit der
Geschwindigkeit 45 km/h. Die Abfahrt erfolgt gleichzeitig.
Wann und wo begegnen sie sich ?
2.
In 10 Std fährt ein Auto von A nach B. Ein anderes Auto fährt von B nach A in 15 Std.
Nach wie viel Stunden begegnen sie sich, wenn sie zugleich abfahren ?
3.
Mit einer Durchschnittsgeschwindigkeit von 48 km/h fährt ein Motorrad um 7 Uhr vom
Ort A ab. Zwei Stunden später folgt ein Pkw mit einer Durchschnittsgeschwindigkeit
von 80 km/h.
Wann und in welcher Entfernung von A wird das Motorrad eingeholt ?
4.
Ein Personenzug, der in 4 min 3 km zurücklegt, fährt von Station A nach Station B.
7 min später geht ein Schnellzug von Station B nach Station A ab, der in 5 min 6 km
fährt. In der Mitte der Strecke begegnen sich beide Züge.
Wie groß ist die Entfernung von A bis B ?
5.
In welcher Zeit fährt ein 300 m langer Eisenbahnzug der 12 m/s schnell ist, durch
einen 180 m langen Tunnel ?
6.
Ein 60 m langer Eilzug fährt mit 72 km/h an einem stehenden Personenzug vorüber.
Die Begegnung dauert 9 s.
Wie lang war der Personenzug ?
7.
In welcher Zeit fahren 2 Züge von 200 und 250 m Länge aneinander vorbei, wenn sie
mit 9 m/s und 13,5 m/s fahren ?
Berechne
a) gleiche Fahrtrichtung und
b) entgegengesetzte Fahrtrichtung.
8.
Ein 60 m langer Eilzug fährt an einem in gleicher Richtung fahrenden 120 m langen
Personenzug mit 72 km/h vorbei. Die Begegnung dauert 18 s.
Welche Geschwindigkeit hat der Personenzug ?
9.
Der große und der kleine Zeiger einer Uhr stehen um 12 Uhr genau übereinander.
Zu welchen Zeiten stehen beide Zeiger noch übereinander ?
10.
Zwei Uhren zeigen gleichzeitig auf 12 Uhr. Eine der beiden Uhren geht je Minute um
1,5 Sekunden vor.
Welche Zeit wird vergehen, bis beide Uhren wieder gleichzeitig auf 12 Uhr zeigen ?
11.
Wenn nach Überschreiten der Mittagszeit beide Zeiger einer Uhr genau einen rechten
Winkel bilden, wie viel Uhr ist es dann ?
Text_03A **** Lösungen 35 Seiten (Text_03L)
1 (6)
www.mathe-physik-aufgaben.de
Realschule / Gymnasium / Berufliche Schulen
Bewegungsaufgaben
12.
Wie viel Minuten nach 4 Uhr holt der Minutenzeiger den Stundenzeiger zum ersten
Mal ein ?
13.
Auf stillstehendem Wasser würde ein Schiff auf der Elbe durch die Kraft seiner
Maschine in jeder Minute 300 m zurücklegen. Es fährt stromaufwärts und erreicht in
1 Std 15min sein Ziel. Für dieselbe Strecke braucht es stromabwärts nur 50 min.
Wie groß ist die Geschwindigkeit des Wassers ?
14.
Die 30 km lange Strecke von Bonn nach Köln fährt ein Rheindampfer stromabwärts
in 1,5 Stunden, flußaufwärts in 2,5 Stunden.
Berechne die Stromgeschwindigkeit und die Eigengeschwindigkeit des Dampfers.
15.
Ein Personenzug fährt um 720 Uhr von einem Bahnhof ab. Mit einer Geschwindigkeit,
die 18 km/h höher ist als die des Personenzuges, fährt um 840 vom gleichen Bahnhof
ein Schnellzug in gleicher Richtung ab. Um 12 Uhr holt er den Personenzug ein. Wie
hoch ist die Geschwindigkeit des Personenzuges, und wie weit ist der Treffpunkt vom
Ausgangsbahnhof entfernt ?
16.
Ein Radfahrer und ein Fußgänger bewegen sich gleichzeitig von A nach B, der eine
legt stündlich 15 km und der andere 5 km zurück. In B hält sich der Radfahrer eine
Stunde auf und trifft auf dem Rückweg den Fußgänger 30 km von B entfernt.
Wie lang ist die Strecke zwischen A und B ?
17.
Zwei Züge kreuzen sich nach 3 Stunden, wenn sie von zwei 270 km voneinander
entfernten Stationen gleichzeitig abfahren. Würde der Zug mit der geringeren
Geschwindigkeit 45 Minuten vor dem anderen abfahren, so würde er diesen
2 Std. 40 Min. nach dessen Abfahrt treffen.
Wie groß ist die jeweilige Geschwindigkeit der Züge ?
18.
Aus einer Entfernung von 39 km gehen zwei Wanderer einander entgegen. Der erste
bricht eine Stunde eher auf als der zweite. Sie treffen sich 3 Stunden nach Aufbruch
des zweiten. Sie wären nach 3 Stunden noch 3 km von einander entfernt, wenn der
erste zur gleichen Zeit wie der zweite aufgebrochen wäre und jeder 0,5 km mehr pro
Stunde zurückgelegt hätte.
Wie groß ist die Geschwindigkeit von beiden ?
19.
Ein Auto fährt einem anderen nach, das 30 Minuten vorher abgefahren ist. Nach
2 Stunden ist es noch 8 km hinter dem ersten, nach weiteren 2 Stunden hat es das
erste Auto um 8 km überholt.
Wie groß ist die jeweilige Geschwindigkeit ?
Wann treffen sich beide Fahrzeuge und wie weit sind sie dann vom Ausgangspunkt
entfernt ?
20.
Ein Güterzug, der um 7 Uhr von A abfährt und in jeder Stunde 22,5 km zurücklegt,
kommt gleichzeitig mit einem Eilzug, der mittags 12 Uhr mit einer Geschwindigkeit
von 60 km/h in A abfährt, in B an.
Wie groß ist die Entfernung von A nach B ?
Text_03A **** Lösungen 35 Seiten (Text_03L)
2 (6)
www.mathe-physik-aufgaben.de
Realschule / Gymnasium / Berufliche Schulen
Bewegungsaufgaben
21.
Die Entfernung München - Frankfurt beträgt 300 km. Um 6 Uhr fährt ein Güterzug von
München ab, der um 18 Uhr in Frankfurt ankommt. Ein Personenzug verläßt um
10 Uhr München in Richtung Frankfurt. Der Personenzug fährt 1,8 mal so schnell wie
der Güterzug.
Wann holt der Personenzug den Güterzug ein, und wann kommt er in Frankfurt an ?
22.
In 3 Stunden fährt ein Motorboot 48,27 km flußabwärts. Für den Rückweg braucht es
5 Stunden.
Wie schnell würde das Boot in stillem Wasser fahren, und wie hoch ist die
Geschwindigkeit der Strömung ?
23.
Von Koblenz nach Köln fährt ein Dampfer in 3 Std. 36 min und von Köln nach Koblenz
in 6 Std. Wie groß sind seine Geschwindigkeit und die des Stromes, wenn die Strecke
Köln-Koblenz 90 km beträgt ? (Koblenz nach Köln ist rheinabwärts)
Wenn der Dampfer rheinaufwärts die Strecke in 5 Std. zurücklegen soll, wie muss sich
die Geschwindigkeit des Schiffes dann ändern?
24.
Ein Zug kommt 20 min zu früh an, wenn er auf einer Fahrt zwischen zwei Stationen
seine fahrplanmäßige Geschwindigkeit um 5 km/h erhöht. Verringert er sie um 5 km/h,
so verspätet er sich um 25 min.
Wie weit sind die Stationen von einander entfernt, und wie groß ist die fahrplanmäßige
Geschwindigkeit ?
25.
Aus 30 km Entfernung gehen 2 Wandergruppen aufeinander zu. Sie treffen sich
2,5 Std. nach dem Aufbruch der zweiten Gruppe, wenn die erste 2 Std. früher aufbricht
als die zweite. Bricht die zweite Gruppe 2 Std. früher auf, so treffen sie sich
3 Std. nach dem Aufbruch der ersten Gruppe.
Wie viel km legt jede Gruppe in einer Stunde zurück ?
26.
Ein Schnellzug braucht auf einer Strecke 2,5 Std. weniger als ein Personenzug, da er
stündlich 25 km mehr als dieser fährt. Ein Güterzug legt stündlich 15 km weniger als
der Personenzug zurück. Er braucht für die Strecke 3,5 Std. mehr als dieser.
Wie lang ist die Strecke, und wie groß sind die Geschwindigkeiten der Züge ?
27.
Mit einer Durchschnittsgeschwindigkeit von 112 km/h fährt ein D-Zug um 8 Uhr von
München in das 82 km entfernte Ingolstadt. Um 8 Uhr 15 Min. fährt ein Personenzug
mit einer Durchschnittsgeschwindigkeit von 68 km/h von Ingolstadt nach München.
Um 8 Uhr 30 Min. fährt ein Güterzug mit einer Durchschnittsgeschwindigkeit von
55 km/h von einem Ort auf der gleichen Strecke, der 30 km von München entfernt ist,
nach Ingolstadt.
a) Geben Sie Ort und Zeit der Begegnung von Personenzug mit D-Zug an.
b) Geben Sie Ort und Zeit der Begegnung von Personenzug mit Güterzug an.
c) Wann müsste der Güterzug abfahren, wenn Güterzug und D-Zug gleichzeitig in
Ingolstadt eintreffen sollen ?
Text_03A **** Lösungen 35 Seiten (Text_03L)
3 (6)
www.mathe-physik-aufgaben.de
Realschule / Gymnasium / Berufliche Schulen
Bewegungsaufgaben
28.
Mit einer Geschwindigkeit von 15 km/h fährt ein Radfahrer einem Fußgänger nach, der
eine Stunde vorher von einem 12 km entfernten Ort A aufgebrochen ist.
Die Geschwindigkeit des Fußgängers ist so bemessen, dass er die Strecke von
A nach B, die 9,4 km beträgt, in 2 Stunden bewältigt.
Welche Strecke muss der Radfahrer zurücklegen, um den Fußgänger einzuholen ?
29.
Ein Ochs und ein Esel wollen einander besuchen. Um 6 Uhr als der Ochs aufbricht,
schickt er eine Wespe zum Esel. Nach 20 Min. Flugzeit trifft diese den Esel, der in
diesem Moment beginnt, mit einer Geschwindigkeit von 3 km/h dem Ochsen
entgegenzutrotten. Sofort fliegt die Wespe wieder zum Ochsen zurück und kehrt, als
sie ihn getroffen hat, im gleichen Moment um und fliegt wieder dem Esel entgegen,
kehrt um, usw.
Die Wespe pendelt zwischen Ochs und Esel hin und her, bis sich schließlich alle drei
treffen. Die Fluggeschwindigkeit der Wespe ist 27 km/h und mit 2 km/h bewegt sich
der Ochse vorwärts.
Wann und wo treffen sich Ochs und Esel ? Wie viele Kilometer ist die Wespe bis zum
Zusammentreffen von Ochs und Esel hin- und hergeflogen ?
30.
Zwei geradlinige Straßen schneiden sich senkrecht. Ein Motorrad fährt in der Stunde
durchschnittlich 60 km. Es durchfährt die Kreuzung in südlicher Richtung.
Ein Kraftwagen, dessen Durchschnittsgeschwindigkeit 90 km/h beträgt, fährt 8 min
später in östlicher Richtung über die Kreuzung.
Wie viele Minuten nach der Durchfahrt des Kraftwagens sind beide Fahrzeuge der
Luftlinie nach 20 km voneinander entfernt ?
31.
Das Laufrad einer Dampflokomotive muss sich auf einer Strecke von 2,160 km
500 mal öfter drehen als das Treibrad, weil der Umfang des ersten um 3 m kleiner
ist als der des zweiten.
Berechne den Umfang der Räder !
32.
Bei der Verfolgung eines flüchtenden Kraftfahrers trennen sich zwei Polizeiwagen an
einer rechtwinkligen Straßenkreuzung. Sie sind über Sprechfunk (Reichweite 30 km)
miteinander im Kontakt. Auf den geradlinig verlaufenden Straßen fahren sie mit
Geschwindigkeiten von 100 km/h bzw. 80 km/h. Der langsamere Wagen sieht nach
15 Minuten den flüchtigen Fahrer vor sich.
Kann der Streifenwagen den anderen zu diesem Zeitpunkt noch über Sprechfunk
erreichen ?
33.
Frühmorgens wandert Arnold von einer Jugendherberge ab. 50 min später verlässt
Berthold die Herberge und holt Arnold nach 12 km um 10 Uhr ein. 50 min nach dem
Einholen ist Berthold bereits 1 km voraus.
Wie viele km legen beide in der Stunde zurück und wann marschierten sie von der
Herberge ab ?
Text_03A **** Lösungen 35 Seiten (Text_03L)
4 (6)
www.mathe-physik-aufgaben.de
Realschule / Gymnasium / Berufliche Schulen
Bewegungsaufgaben
34.
Ein Radfahrer fährt um 7 Uhr von A nach dem 146 km entfernten B ab;
ein Mopedfahrer startet um 8 Uhr von B nach A. In der Stunde legt der Mopedfahrer
20 km mehr zurück als der Radfahrer. In 90 km Entfernung von B treffen sie sich.
Welche Geschwindigkeit hat jeder und um wie viel Uhr treffen sie sich ?
35.
Ein Eilzug braucht zum Durchfahren einer 225 km langen Strecke 3,5 Stunden
weniger als ein Personenzug. Dabei legt der Eilzug 26,25 Kilometer in der Stunde
mehr zurück als der Personenzug.
Wie groß sind Geschwindigkeit und Fahrtdauer beider Züge ?
36.
Mit 5 km/h geht ein Fußgänger von A nach B. Er wird 90 Minuten nach seinem
Aufbruch von einem Radfahrer überholt, der eine halbe Stunde nach dieser
Begegnung in B ankommt, dort sofort wendet und in A zu derselben Zeit ankommt,
in welcher der Fußgänger B erreicht.
Wie groß ist die Entfernung zwischen A und B ?
Wie groß ist die Durchschnittsgeschwindigkeit des Radfahrers ?
37.
Ein Rheindampfer fährt von Bingen um 12 Uhr mit 18 km/h Geschwindigkeit ab.
Um 14 Uhr begegnet er einem Dampfer, der Koblenz um 12 Uhr verlassen hat.
Der erste kommt 1 Std. 40 min früher in Koblenz an als der zweite in Bingen.
Wie lang ist die Fahrtstrecke ?
38.
Ein Eisenbahnzug kann jetzt durch Verbesserung der Strecke eine um 9 km höhere
Durchschnittsgeschwindigkeit erreichen als vorher und erzielt dadurch auf einer
Strecke von 180 km eine Zeiteinsparung von 40 min.
Wie viel Stunden benötigte er für die Strecke vorher ?
39.
Zwei Häfen A und B sind 100 km von einander entfernt. Von diesen beiden Häfen
fahren ein Dampfer und ein Segelboot zur gleichen Zeit ab. Mit einer konstanten
Geschwindigkeit von 45 km/h fährt der Dampfer von A nach B. Das Segelboot fährt
von B aus senkrecht zur Verbindungsstrecke AB mit einer Geschwindigkeit von
15 km/h.
Nach welcher Zeit ist die Entfernung zwischen dem Dampfer und dem Segelboot am
kleinsten ?
40.
Ein Flugzeug verspätet sich auf der Strecke München-London (945 km) wegen
Gegenwind mit v = 17,5 m/s um 10 Minuten. Welche Geschwindigkeit hat das
Flugzeug bei Windstille ? Wie lang ist die Flugzeit bei Gegenwind ?
41.
Ein Auto fährt eine Strecke von 120 km.
Mit einer um 20 km/h größeren Geschwindigkeit durchfährt ein zweites Auto die
gleiche Strecke und braucht 1 Stunde weniger Zeit.
Wie groß sind die Geschwindigkeiten beider Autos ?
Text_03A **** Lösungen 35 Seiten (Text_03L)
5 (6)
www.mathe-physik-aufgaben.de
Realschule / Gymnasium / Berufliche Schulen
Bewegungsaufgaben
42.
Mit jeweils gleichförmigen Geschwindigkeiten fahren einander zwei Züge entgegen.
Zug 1 fährt 20 Minuten früher in A weg als Zug 2 in B. Der Ort der Begegnung liegt
15 km näher an B als an A. Nach der Begegnung benötigt Zug 1 noch 48 Minuten
um nach B zu kommen, dagegen Zug 2 noch 50 Minuten bis zu seiner Ankunft in A.
Gesucht sind die Geschwindigkeiten der Züge.
43.
Von Ort A fährt ein Radfahrer nach dem 60 km entfernten Ort B. Auf dem Heimweg
kommt Rückenwind auf. Bei der Heimfahrt ist dadurch die durchschnittliche
Geschwindigkeit um 4 km/h größer und die Fahrzeit um 30 Minuten kürzer als bei der
Hinfahrt.
Welche Zeit braucht der Radfahrer für die Hinfahrt ? Wie groß ist die Durchschnittsgeschwindigkeit bei der Rückfahrt ?
44.
Auf einer geschlossenen Rennbahn starten zwei Personen mit Rollschuhen in
entgegengesetzte Richtungen. Sie begegnen sich nach 40 Sekunden. Für eine ganze
Runde benötigt der Sieger 18 Sekunden weniger als der zweite.
In welcher Zeit durchfährt jeder eine Runde ?
45.
Zwei Fahrer starten gleichzeitig auf einer Radrennbahn in gleicher Richtung.
Der langsamere Fahrer wird nach 10 min 50 s überrundet. Zu einer Runde braucht
der schnellere Fahrer eine Sekunde weniger Zeit als der langsamere.
Welche Zeit benötigt jeder Fahrer für eine Runde ?
46.
Von zwei Orten A und B fahren zwei Radfahrer einander gleichzeitig entgegen. Die
Geschwindigkeiten der Radfahrer sind konstant, aber verschieden groß. An einem
Punkt, der 1 560 m vom nächstliegenden Ort entfernt ist, begegnen sie sich. Nachdem
beide Radfahrer den gegenüberliegenden Ort erreicht haben, legen sie
eine Pause von jeweils 15 Minuten ein, bevor sie zu ihren Ausgangsorten
zurückfahren. Sie treffen sich auf dem Rückweg 600 m vom anderen Ort entfernt.
Wie groß ist die Entfernung zwischen beiden Orten ?
Text_03A **** Lösungen 35 Seiten (Text_03L)
6 (6)
www.mathe-physik-aufgaben.de