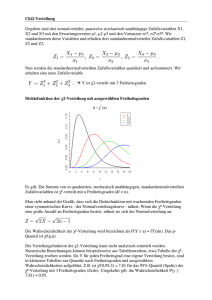
Zweiseitiger Test für den unbekannten Mittelwert µ einer

Zweiseitiger Test für den unbekannten Mittelwert µ
einer Normalverteilung bei unbekannter Varianz
Grundlage:
Die Testvariable T =
X − µ0
√
S/ n
genügt der t-Verteilung mit n − 1 Freiheitsgraden.
Auf der Basis einer Zufallsstichprobe x1 , x2 , . . . , xn vom Umfang n soll die
Nullhypothese H0 : µ = µ0
gegen die
Alternativhypothese H1 : µ 6= µ0
getestet werden.
Vorgehensweise:
1) Auswahl einer Signifikanzzahl α (meist α = 0.05 oder α = 0.01)
2) Berechnung des kritischen Wertes c aus der Bedingung 2F (c) − 1 = 1 − α,
wobei F die Verteilungsfunktion
der t-Verteilung mit n − 1 Freiheitsgraden
bezeichnet, d.h. c ist das
1−
α
2
-Quantil der t-Verteilung
mit n − 1 Freiheitsgraden ⇒ nicht-kritischer Bereich: −c ≤ t ≤ c
3) Berechnung des Mittelwertes x und der Standardabweichung s der konkreten
Stichprobe x1 , x2 , . . . , xn sowie des Test- oder Prüfwertes:
t̂ =
x − µ0
√
s/ n
4) Testentscheidung: Fällt der Test- oder Prüfwert t̂ in den nicht-kritischen
Bereich, d.h. gilt −c ≤ t̂ ≤ c, dann wird die Nullhypothese H0 nicht abgelehnt.
Anderenfalls wird sie zugunsten der Alternativhypothese H1 abgelehnt.
Mathematik III - Folie 61
Zweiseitiger Test für die Gleichheit der unbekannten Mittelwerte
µ1 und µ2 zweier NV unter Verwendung abhängiger Stichproben
Voraussetzungen: Die ZV X und Y seien normalverteilt mit den Mittelwerten µ1
und µ2 . Es liegen zwei abhängige Stichproben x1 , x2 , . . . , xn und y1 , y2 , . . . , yn vor.
Auf der Basis dieser Stichproben soll die Nullhypothese H0 : µ1 = µ2 gegen die
Alternativhypothese H1 : µ1 6= µ2 getestet werden (zweiseitiger Parametertest).
Vorgehensweise:
Dieser Parametertest wird auf einen Test des Hilfsparameters µ = µ1 − µ2
zurückgeführt. Dann wird die Nullhypothese H0 : µ = 0 gegen die
Alternativhypothese H1 : µ 6= 0 getestet.
Dazu werden aus den beiden abhängigen Stichproben die Differenzen zi = xi − yi
(i = 1, 2, . . . , n) gebildet. Diese werden als Stichprobenwerte einer neuen Stichprobe vom Umfang n betrachtet: z1 , z2 , . . . , zn . Mittels der auf Folie 60 bzw. 61
erläuterten Vorgehensweise (bezogen auf die Stichprobe z1 , z2 , . . . , zn ) kann
über die Nichtablehnung oder Ablehnung der Hypothese H0 : µ = 0
entschieden werden.
Dabei ist zu beachten: sind die Varianzen der Zufallsvariablen X und Y bekannt
oder gilt für den Stichprobenumfang n > 30, ist die auf Folie 60 beschriebene
Vorgehensweise anwendbar. Anderenfalls ist so vorzugehen wie auf Folie 61
beschrieben.
Mathematik III - Folie 62
Ein Beispiel für einen zweiseitiger Test für die Gleichheit der unbekannten
Mittelwerte zweier NV unter Verwendung abhängiger Stichproben
Beispiel 15.10:
Zwei verschiedene Messmethoden für elektrische Widerstände sollen miteinander verglichen werden. Dazu wurden an 6 Widerständen Parallelmessungen
durchgeführt, deren Ergebnisse in dem folgenden Messprotokoll dargestellt sind
(xi : Messwerte nach der Methode A, yi : Messwerte nach der Methode B).
i
1
2
3
4
5
6
xi /Ω
100.5
102.0
104.3
101.5
98.4
102.9
yi /Ω
98.2
99.1
102.4
101.1
96.2
101.8
Zu jedem der 6 Widerstände gehört genau ein Wertepaar (xi , yi ). Daher handelt
es sich um abhängige Stichproben. Durch Differenzbildung zi = xi − yi ergibt sich
als neue Stichprobe:
i
1
2
3
4
5
6
zi /Ω
2.3
2.9
1.9
0.4
2.2
1.1
Die beiden Messmethoden A und B werden als gleichwertig angesehen,
wenn diese Stichprobe aus einer (normalverteilten) Grundgesamtheit mit dem
Mittelwert µ = 0 stammt.
Mathematik III - Folie 63
Zweiseitiger Test für die Varianz einer Normalverteilung
Die Nullhypothese H0 : σ 2 = σ02 soll gegen die Alternativhypothese H1 : σ 2 6= σ02
getestet werden.
Grundlage: Die Zufallsvariable Z =
S2
(n − 1) 2
σ0
genügt der Chi-Quadrat-Verteilung
mit n − 1 Freiheitsgraden.
Vorgehensweise:
1) Festlegung einer Signifikanzzahl (Irrtumswahrscheinlichkeit) α
(üblicherweise: α = 0.05 od. α = 0.01)
2) Berechnung der Konstanten c1 und c2 aus den Bedingungen F (c1 ) =
α
2
α
2
und
(F : Verteilungsfunktion der Chi-Quadrat-Verteilung mit n − 1
α
α
Freiheitsgraden). Die Zahlen c1 bzw. c2 sind das - bzw. 1 −
-Quantil
F (c2 ) = 1 −
2
2
der Chi-Quadrat-Verteilung mit n − 1 Freiheitsgraden.
⇒ nicht-kritischer Bereich: c1 ≤ z ≤ c2
3) Berechnung der Varianz s2 der vorgeg. Stichprobe sowie des Testwertes:
s2
ẑ = (n − 1) 2
σ0
4) Testentscheidung: Fällt der Test- oder Prüfwert ẑ in den nicht-kritischen
Bereich, d.h. gilt c1 ≤ ẑ ≤ c2 , dann wird die Nullhypothese H0 nicht abgelehnt.
Anderenfalls wird sie zugunsten der Alternativhypothese H1 abgelehnt.
Mathematik III - Folie 64
Chi-Quadrat-Test zur Überprüfung einer Hypothese über die unbekannte
Verteilungsfunktion einer Grundgesamtheit
Die Nullhypothese H0 : F (x) = F0 (x) soll gegen die
Alternativhypothese H1 : F (x) 6= F0 (x) getestet werden.
Vorgehensweise:
1) Unterteilung der n Stichprobenwerte in k Klassen (Intervalle) I1 , I2 , . . . , Ik
und Feststellung der absoluten Klassenhäufigkeiten n1 , n2 , . . . , nk
2) Für jede Klasse Ii : mit Hilfe von F0 (x) die Wahrscheinlichkeit pi und
die Anzahl n∗i = npi der theoretisch erwarteten Stichprobenwerte berechnen
3) Berechnung des Testwertes
ẑ = χ̂2 =
k
X
(ni − n∗ )2
i
i=1
n∗i
=
k
X
(ni − npi )2
i=1
npi
4) Auswahl einer Signifikanzzahl α (meist α = 0.05 oder α = 0.01) und Bestimmung der kritischen Grenze c. Diese ist das (1 − α)-Quantil der Chi-QuadratVerteilung mit k − 1 Freiheitsgraden.
⇒ nicht-kritischer Bereich: z = χ2 ≤ c
5) Testentscheidung: Fällt der Test- oder Prüfwert ẑ = χ̂2 in den nichtkritischen Bereich, d.h. gilt ẑ = χ̂2 ≤ c, dann wird die Nullhypothese H0
nicht abgelehnt. Anderenfalls wird sie zugunsten der Alternativhypothese H1
abgelehnt.
Mathematik III - Folie 65
Ein Beispiel zum Chi-Quadrat-Test
Beispiel 15.11:
Bei 120 Würfen mit einem homogenen Würfel ergaben sich die folgenden Häufigkeiten:
i
1
2
3
4
5
6
abs. Häufigk. ni
15
19
22
21
17
26
Die Nullhypothese H0 : ”Alle 6 möglichen Augenzahlen sind gleichwahrscheinlich.” soll mit Hilfe
des Chi-Quadrat-Tests überprüft werden.
Bei der Einteilung der Stichprobenwerte in Klassen wird k = 6 gewählt; die Klassen entsprechen
genau den Augenzahlen. Gemäß der Hypothese H0 gilt: pi = 1/6.
Klasse
(Augenz. i)
ni
pi
1
15
1/6
20
-5
25/20
2
19
1/6
20
-1
1/20
3
22
1/6
20
2
4/20
4
21
1/6
20
1
1/20
5
17
1/6
20
-3
9/20
6
26
1/6
20
6
36/20
Σ
120
1
120
0
76/20
n∗i
= npi
∆ni = ni −
n∗i
(∆ni )2
n∗i
Berechnung der Testgröße: ẑ = χ̂2 = 76/20 = 3.8; Festlegung der Signifikanzzahl: α = 0.05;
1 − α = 0.95-Quantil der Chi-Quadrat-Verteilung mit k − 1 = 5 Freiheitsgraden: c = 11.07
⇒ nicht-kritischer Bereich: z = χ2 ≤ 11.07
Da ẑ = χ̂2 ≤ 11.07 gilt, wird die Hypothese H0 nicht abgelehnt.
Mathematik III - Folie 66