Vorschrift

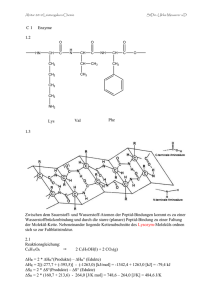
Grundpraktikum
Physikalische Chemie
Versuch 14:
Ladungstransport
überarbeitet: Tobias Staut, 2013.04
Inhaltsverzeichnis
1 Vorbereitung und Eingangskolloquium
3
2 Theorie
5
2.1
Ladungstransport in starken Elektrolytlösungen . . . . . . . . . . . . . . . .
5
2.2
Debye-Hückel-Onsager Korrekturen . . . . . . . . . . . . . . . . . . . . . . .
7
2.3
Ladungstransport in schwachen Elektrolytlösungen . . . . . . . . . . . . . .
8
2.4
Theorie vom Ladungstransport über Wasserstoffbrücken . . . . . . . . . . . 10
3 Versuchsdurchführung
13
3.1
Teil A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
3.2
Teil B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
Grundpraktikum Physikalische Chemie 2013
14 - Ladungstransport
1 Vorbereitung und Eingangskolloquium
Bereiten Sie folgende Themengebiete vor:
• Ladungstransport in Elektrolytlösungen
• Ladungstransport in schwachen Elektrolytlösungen
• Ladungstransport über Wasserstoffbrücken
Die gründliche theoretische Vorbereitung dieser Themengebiete ist unumgänglich zum Verständnis und zur sicheren Durchführung des Versuches!
3/13
Grundpraktikum Physikalische Chemie 2013
14 - Ladungstransport
Kolloqiumsfragen:
So oder so ähnlich werden die gestellten Fragen aussehen. Richten Sie Ihre Vorbereitung
daran aus. (∗) kennzeichnet Kernfragen.
(i) Was ist elektrischer Strom? Mechanismen des Ladungstransports? Wie werden Elektrolyte unterschieden? (∗)
(ii) Was bewirkt ein elektrisches Feld?
(iii) In den Herleitungen werden einige Annahmen und Näherungen gemacht. Nennen Sie
zwei. (∗)
(iv) Ist die Ionenbeweglichkeit u eine Materialkonstante?
(v) Wie wird die spezifische Leitfähigkeit κ gemessen? Skizzieren Sie den Versuchsaufbau
und schildern Sie ihr Vorgehen. (∗)
(vi) Ist die Messung von κ direkt oder indirekt?
(vii) Wovon hängt κ ab? Hinweis: (2.4) und (2.10) (∗)
(viii) Warum wird die Äquivalentleitfähigkeit eingeführt?
(ix) Wie entsteht eine Nahordnung in realen Lösungen?
(x) Skizzieren Sie ein Ion samt Ionenwolke ohne äußeres Feld. Welche Kräfte wirken auf
das System, wenn ein äußeres Feld angelegt wird? (∗)
(xi) Was bestimmt den Dissoziationsgrad α?
(xii) Wieso werden zur Bestimmung der Dissoziationsgrade der schwachen Säuren die
Äquivalentleitfähigkeiten der starken Säuren und ihrer Salze verwendet?
(xiii) Beschreiben Sie die graphische Auswertung des Versuchs. Was wird gemessen? Welche
sind die Zielgrößen? Welche Gleichungen liegen zu Grunde? (∗)
(xiv) Laut (2.4) und (2.10) ist κ umgekehrt proportional zum Ionenradius. Warum gilt
dies nicht für Alkalimetalle?
(xv) Beschreiben Sie den Grotthuß-Mechanismus.
(xvi) Warum verringern geringe Mengen H2 O die Leitfähigkeit von Alkoholen?
4/13
Grundpraktikum Physikalische Chemie 2013
14 - Ladungstransport
2 Theorie
2.1 Ladungstransport in starken Elektrolytlösungen
Abbildung 1: Gefäß zur Messung der Elektrolytlösungen im elektrischen Feld.
Wir betrachten eine Elektrolytlösung, die sich in einem Gefäß der Länge l und mit Seitenflächen A befindet, wie es in Abb. 1 dargestellt ist. An dessen Stirnseiten sind zwei
Elektroden gleicher Fläche angebracht. Wird an diese Elektroden die Gleichspannung U
angelegt, dann herrscht im Inneren der Lösung die Feldstärke
E=
U
.
l
(2.1)
In dem elektrischen Feld werden die Ionen beschleunigt, und zwar die Anionen zur positiven, die Kationen zur negativen Elektrode hin. Auf ein Ion der Ladung q = ze (mit e der
Elementarladung; z ∈ Z) wirkt die elektrische Kraft
Fel = q · E = zeE.
(2.2)
Durch diese Kraft werden die Ionen beschleunigt. Ihre Geschwindigkeit wächst so lange an,
bis die durch (2.2) gegebene Kraft genauso groß ist, wie die in entgegengesetzter Richtung
wirkende Reibungskraft FR . Unter der Annahme, dass sich die Ionen wie starre Kugeln mit
dem Radius r in einer viskosen Flüssigkeit verhalten, gilt das stokessche Reibungsgesetz:
FR = 6πηrv.
(2.3)
Dabei ist η die Viskosität des Lösungsmittels und v die Geschwindigkeit der Ionen. Gleichsetzen von (2.2) und (2.3) liefert für die Geschwindigkeit v
v=
ze
E = uE.
6πηr
5/13
(2.4)
Grundpraktikum Physikalische Chemie 2013
14 - Ladungstransport
Die Geschwindigkeit v ist also zum elektrischen Feld proportional. Die Proportionalitätskonstante u hängt nur vom betrachteten Ion und dem Lösungsmittel ab; u heißt Ionenbeweglichkeit.
Das Wandern der Ionen führt zu einem Strom I im Stromkreis. Ist ∆Q die Ladung derjenigen Ionen, die in der Zeit ∆t durch den Querschnitt A des Gefäßes treten, dann ist
∆Q
.
∆t
(2.5)
∆x = v∆t
(2.6)
I=
In der Zeit ∆t legt jedes Ion den Weg
zurück. Alle Ionen, die sich im Volumen A · ∆x befinden, wandern in der Zeit ∆t durch
den Querschnitt A des Gefäßes. Ist n =
N
V
die Teilchenzahldichte der Ionen, dann ist
∆Q = zen · A∆x = zen · Av∆t.
Daraus folgt mit c =
(2.7)
n
NA
I = eNA · czAv = F · cz
A
uU .
l
(2.8)
Mit c der Konzentration, NA der Avogadrokonstanten und F = eNA der Faradykonstanten.
Der Strom I ist nach (2.8) proportional zur Spannung U . Die Größe
κ=
I l
·
U A
(2.9)
heißt spezifische Leitfähigkeit der Lösung. κ lässt sich aus I, U und den Abmessungen der
Messzelle experimentell bestimmen.
Nach (2.8) hängt κ im betrachteten Modell von der Konzentration c und der Ionenbeweglichkeit u ab:
κ = F · c · z · u.
(2.10)
Diese Überlegungen beziehen sich auf den Fall, dass nur eine Ionensorte zur Leitfähigkeit
beiträgt; im Allgemeinen wandern jedoch mehrere Ionensorten im elektrischen Feld.
Wir wollen den Fall betrachten, dass ein Elektrolyt in zwei Ionensorten zerfällt. Dann gilt
κ = F (c+ · z+ · u+ + c− · z− · u− )
6/13
(2.11)
Grundpraktikum Physikalische Chemie 2013
14 - Ladungstransport
an Stelle von (2.10).
Aus Elektroneutralitätsgründen ist c+ z+ = c− z− , und daher gilt im Rahmen des Modells
κ = F · c+ z+ (u+ + u− ).
Die Größe Λ =
κ
c+ z+
(2.12)
wird als Äquivalentleitfähigkeit bezeichnet. In unserem Modell ist
also:
Λ = F · (u+ + u− ).
(2.13)
(2.13) ist von der Konzentration c unabhängig. Dies trifft jedoch nur im Grenzfall unendlicher Verdünnung zu. Aus diesem Grund wird Λ durch Λ0 (Äquivalentleitfähigkeit bei
unendlicher Verdünnung) ersetzt:
Λ0 = F · (u+ + u− ).
(2.14)
Bei realen Lösungen bewirken die elektrostatischen Anziehungskräfte der Ionen untereinander, dass jedes Ion bevorzugt von Gegenionen umgeben ist (→ Nahordnung). Ohne äußeres
Feld ist die Anordnung im Mittel kugelsymmetrisch. Wird die Kugelsymmetrie aufgehoben,
entstehen zusätzliche Kräfte, die die molare Leitfähigkeit verringern. Sie sind umso stärker,
je höher konzentriert die Elektrolyte sind. Diese Kräfte sollen jetzt für starke Elektrolyte
(d.h. für Salze, die vollständig dissoziieren) näher beschrieben werden.
2.2 Debye-Hückel-Onsager Korrekturen
Zwei Effekte reduzieren die molare Leitfähigkeit.
• Der elektrophoretische Effekt Λe :
Jedes Ion ist von einer Ionenwolke umgeben. Diese hat eine dem Zentralion entgegengesetzte Ladung, und bewegt sich daher im Feld auch in die andere Richtung. Es
entsteht Reibung, die die Beweglichkeit des Ions verringert.
• Der Relaxationseffekt Λr :
Durch die Bewegung im äußeren Feld wird das Ion aus seiner Ruhelage im Zentrum
der Ionenwolke ausgelenkt. Ein lokales elektrisches Feld übt nun eine Kraft auf das
Ion aus, welche wiederum dessen Beweglichkeit reduziert.
Beide Effekte sind proportional zu
√
c, so dass die Debye-Hückel-Onsager Korrekturen das
kohlrauschsche Quadratwurzelgesetz (2.15) theoretisch erklären:
7/13
Grundpraktikum Physikalische Chemie 2013
Λ
=
=
14 - Ladungstransport
Λ 0 − Λe − Λr
√
Λ0 − k · c.
(2.15)
Um die Ionenbeweglichkeiten u+ und u− aus Λ0 zu berechnen, müssen wir aus den Messwerten für Λ – die bei endlichen Ionenkonzentrationen gewonnen werden – auf Λ0 extra√
polieren. Dazu wird Λ in Abhängigkeit von c auftragen; nach (2.15) erwarten wir dann
eine Gerade, und der Achsenabschnitt ergibt Λ0 .
Beachten Sie, dass diese Herleitung nur für starke Elektrolyte gilt, d.h. für Salze, die als
völlig dissoziiert betrachtet werden können.
2.3 Ladungstransport in schwachen Elektrolytlösungen
In den vorangehenden Betrachtungen haben wir uns mit starken Elektrolyten beschäftigt,
die vollständig in Ionen dissoziieren (z.B. NaCl). Jetzt wollen wir die Leitfähigkeit von
schwachen Elektrolyten untersuchen. Als Beispiel wählen wir Essigsäure (HAc), die in H+ Ionen und Acetat-Ionen Ac− dissoziiert,
+
−
−
*
HAc −
)
−
− H + Ac .
(2.16)
Dabei stellt sich ein Gleichgewicht ein, das über die Gleichgewichtskonstante K beschrieben
werden kann. Ist C die Gleichgewichtskonzentration der Ionen (= Konzentration von H+
= Konzentration von Ac– ) und ist c0 die Gesamtkonzentration an Essigsäure, dann ist
K=
C2
.
c0 − C
(2.17)
C
c0
(2.18)
Den Bruchteil
α=
aller Essigsäuremoleküle, die dissoziiert vorliegen, wird Dissoziationsgrad genannt.
Eine Auftragung von α gegen c0 für verschiedene Werte von K zeigt, dass α mit steigender
Konzentration c0 drastisch abnimmt. Infolgedessen hängt auch die spezifische Leitfähigkeit
κ in komplizierter Weise mit c0 zusammen.
Im Fall der Essigsäure ist die Ionenkonzentration C so gering, dass das einfachste Leitfähigkeitsmodell (d.h. keine Wechselwirkungen zwischen den Ionen) anwendbar ist. Es gilt
also nach (2.12) für die spezifische Leitfähigkeit (mit c+ = C und z+ = 1)
8/13
Grundpraktikum Physikalische Chemie 2013
14 - Ladungstransport
κ = F · C · (u+ + u− ).
(2.19)
Durch Messung der spezifischen Leitfähigkeit kann der Dissoziationsgrad α der Essigsäure
berechnet werden:
α=
κ
C
=
.
c0
F · (u+ + u− ) · c0
(2.20)
Zur Bestimmung der Größe
(u+ + u− ) = (uH+ + uAc− )
(2.21)
in (2.20) werden die Äquivalentleitfähigkeiten Λ0 von NaCl-, NaAc- und HCl-Lösungen
herangezogen:
Λ0,NaCl = F · (uNa+ + uCl− )
(2.22)
Λ0,NaAc = F · (uNa+ + uAc− )
(2.23)
Λ0,HCl = F · (uH+ + uCl− ).
(2.24)
Daraus folgt:
uH+ + uAc− =
1
· (Λ0,HCl + Λ0,NaAc − Λ0,NaCl ) .
F
(2.25)
Nach (2.20) und (2.25) kann jetzt C für verschiedene Werte von c0 durch Messung der
spezifischen Leitfähigkeit ermittelt werden. Mit diesen Wertepaaren ergibt sich nach (2.17)
die Dissoziationskonstante der Essigsäure.
9/13
Grundpraktikum Physikalische Chemie 2013
14 - Ladungstransport
2.4 Theorie vom Ladungstransport über Wasserstoffbrücken
Die Kapitel soll einen kurzen Überblick über den wichtigen Grotthuß-Mechanismus geben.
Abbildung 2: Wanderung einer positiven Ladung über Wasserstoffbrücken.
In Abschnitt 2.1 wird die Leitfähigkeit von Elektrolytlösungen darauf zurückgeführt, dass
die Ionen wie geladene Kugeln durch die Lösung wandern. Für die meisten Ionen trifft
diese Vorstellung weitgehend zu. Bei dem H+ -Ion (bzw. H3 O+ -Ion) und dem OH– -Ion ist
die Ionenbeweglichkeit allerdings viel größer als aufgrund der Molekülgröße zu erwarten.
Deshalb wird angenommen, dass in diesen Fällen das Ion selbst gar nicht wandert, sondern
dass nur die positive bzw. negative Ladung über Wasserstoffbrücken weitertransportiert
wird.
Dazu betrachten wir Abb. 2. Zunächst lagert sich ein Proton am linken Ende der Kette
von H2 O-Molekülen an. Durch Umwandlung einer normalen Bindung in eine Wasserstoffbrückenbindung gelangt die Ladung an das zweite Molekül usw. Zur Umwandlung einer
normalen Bindung in eine Wasserstoffbrückenbindung ist nur eine geringe Aktivierungsenergie nötig, wenn gleichzeitig an einer benachbarten Stelle aus einer Wasserstoffbrückenbindung eine normale Bindung entsteht. In einem elektrischen Feld kann diese Art des
Ladungstransports gegenüber der Ionenwanderung überwiegen. Der H3 O+ -Komplex, der
sich in Abb. 2 anscheinend bewegt, wird Soliton genannt. Außer Wasser weisen Alkoho-
10/13
Grundpraktikum Physikalische Chemie 2013
14 - Ladungstransport
le diesen Effekt auf. In diesem (optionalen) Teil des Versuchs wird die Leitfähigkeit von
Alkohol-Wasser Mischungen experimentell untersucht.
Obwohl die Leitfähigkeit von Wasser größer ist als die von Alkohol, sinkt die Leitfähigkeit
der Lösung, wenn zu wasserfreiem Alkohol geringe Mengen Wasser hinzufügt werden. Das
liegt daran, dass das Gleichgewicht
+
−−
*
ROH+
−
− ROH + H3 O
2 + H2 O )
(2.26)
auf der rechten Seite liegt, weil Wasser eine stärkere Base als Alkohol ist. Die Protonen
werden im Alkohol auf diese Weise von den H2 O-Molekülen gebunden. Damit elektrische
Leitung in dem Alkohol stattfinden kann, müsste die H-OH+
2 -Bindung gelöst werden. Dazu
ist aber eine viel zu hohe Energie erforderlich. Erst bei genügend hoher Konzentration des
Wassers findet Leitung über die Wassermoleküle statt, so dass dann die Leitfähigkeit der
Lösung wieder ansteigt. Eine Messung der Leitfähigkeit bei verschiedenen Konzentrationen
an Wasser ermöglicht die Berechnung der Gleichgewichtkonstante K der Reaktion (2.26).
Bei kleinen Konzentrationen an H2 O kann die Konzentrationen an ROH als konstant ansehen werden und in die Gleichgewichtskonstante miteinbeziehen; dann gilt
K=
CH 3 O +
CH 2 O
· CROH+ .
(2.27)
2
Falls CH3 O+ << CH2 O ist, ist CH2 O durch cH2 O (Einwaagekonzentration an H2 O) gegeben.
Zu der Lösung von H2 O in ROH wird eine geringe Menge HCl hinzugefügt. Dann gilt
CH3 O+ + CROH+ = cCl− ,
(2.28)
2
da dann praktisch alle Protonen in der Lösung von der HCl herrühren. Damit folgt aus
(2.27)
CH3 O+ = cCl− ·
CH 2 O · K
1 + CH 2 O · K
(2.29)
und
CROH+ = cCl− ·
2
1
1 + CH 2 O · K
.
(2.30)
Für die spezifische Leitfähigkeit κ der Lösung gilt, falls cH2 O und cCl− genügend klein sind,
i
h
κ = F · cCl− · uCl− + cH3 O+ · uH3 O+ + cROH+ · uROH+ .
2
11/13
2
(2.31)
Grundpraktikum Physikalische Chemie 2013
14 - Ladungstransport
Dabei ist F die Faradaykonstante und u die Beweglichkeit. Wir nehmen an, dass auch hier
die Geschwindigkeit, mit der eine Ladung transportiert wird (d.h. die Geschwindigkeit der
Solitonen) zur elektrischen Feldstärke proportional ist. Dann gelten die in Abschnitt 2.1
gegebenen Beziehungen für κ auch hier. Einsetzen von (2.29) und (2.30) ergibt
κ = F · cCl− · uCl−
CH 2 O · K
1
+
·u
·u
+ .
+ +
1 + CH 2 O · K H 3 O
1 + CH2 O · K ROH2
(2.32)
Wir addieren in der Klammer „die Null“, also
CH 2 O · K
CH 2 O · K
,
·u
·u
+ −
+
1 + CH2 O · K ROH2
1 + CH2 O · K ROH2
(2.33)
dann folgt
κ = F · cCl− · (uCl− + uROH+ ) + F · cCl− · (uH3 O+ − uROH+ ) ·
2
2
1
cH
2
K
.
+K
O
(2.34)
Dabei wurde CH2 O = cH2 O gesetzt, weil cHCl << cH2 O ist. Im Fall cH2 O → 0 (wasserfreier
Alkohol) geht
1
cH O
gegen Unendlich, und κ ist durch den Summanden in (2.34) gegeben. Da
2
bei kleinen H2 O-Konzentrationen uH3 O− viel kleiner ist als uROH+ , ist der zweite Summand
2
in (2.34) negativ. Die Erwartung ist also, dass nach Zugabe von Wasser zum Alkohol (d.h.
Zunahme von cH2 O ) κ abnimmt.
Wir wollen (uCl− +uROH+ ), (uH3 O+ −uROH+ ) und K aus (2.34) ermitteln. Zur Bestimmung
2
2
von (uCl− + uROH+ ) wird κ gegen cH2 O aufgetragen. Extrapolation der erhaltenen Kurve
2
für cH2 O → 0 ergibt für die spezifische Leitfähigkeit κ0 in wasserfreiem Alkohol
κ0 = F · cCl− · (uCl− + uROH+ ).
(2.35)
2
Zur Bestimmung von (uH3 O+ − uROH+ ) und von K wird (2.34) umgeformt
2
cH2 O
1
=
κ − κ0
F · cCl− · (uH3 O+ − vROH+ )
2
Bei einer Auftragung von
cH O
2
(κ−κ0 )
1
cH2 O +
K
.
(2.36)
in Abhängigkeit von cH2 O , ergibt sich eine Gerade. Aus
der Steigung wird (uH3 O+ −uROH+ ), aus dem Achsenabschnitt die Gleichgewichtskonstante
2
K bestimmt.
12/13
Grundpraktikum Physikalische Chemie 2013
14 - Ladungstransport
3 Versuchsdurchführung
Lesen Sie sich aufmerksam die Anleitung durch und machen Sie sich mit dem Versuchsaufbau vertraut, bevor Sie mit dem Versuch beginnen.
Zuerst muss das Konduktometer auf die Temperatur kalibriert werden, bei der die Messungen stattfinden. Zu diesem Zweck wird eine Kalibrierlösung vermessen, die eine bekannte temperaturabhängige Leitfähigkeit besitzt. Der auf 25 ◦ C korrigierte Leitfähigkeitswert
kann nun dem Messgerät übergeben werden. Die folgenden Messungen werden im „korrigierte Modus“ durchgeführt.
3.1 Teil A
Die auf 25 ◦ C korrigierten spezifischen Leitfähigkeiten von wässrigen HCl-, NaCl- und
NaAc-Lösungen werden bei 10 Konzentrationen c zwischen 10−4 und 10−2 mol/l gemessen.
Die Äquivalentleitfähigkeit Λ wird berechnet und in Abhängigkeit von
√
c aufgetragen.
Aus dem Achsenabschnitt der erhaltenen Geraden wird die Äquivalentleitfähigkeit Λ0 bei
unendlicher Verdünnung bestimmt.
3.2 Teil B
Die auf 25 ◦ C korrigierten spezifischen Leitfähigkeiten von wässrigen Essigsäurelösungen bei
10 verschiedenen Konzentrationen c zwischen 10−4 und 10−2 mol/l werden gemessen. Daraus
wird der Dissoziationsgrad α in Abhängigkeit von c0 ermittelt (graphische Darstellung).
Mit diesem Wert sowie den Ergebnissen aus Teil A wird die Dissoziationskonstante K von
Essigsäure bestimmt. Dazu wird K für jedes Messwertpaar (κ, c0 ) nach (2.17) und (2.20)
berechnet. Die Werte werden mit Gewichtung gemittelt, indem K in Abhängigkeit von c0
aufgetragen und eine Ausgleichsgerade parallel zur c0 Achse bestimmt wird.
13/13