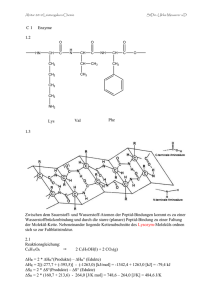
Ionisation

Massenspektrometrie
Seminar WiSe 2015/2016
PD Dr. Markus Nett
Nachwuchsgruppenleiter
L ib i I i für
Leibniz‐Institut
fü Naturstoff‐Forschung
N
ff F
h
und Infektionsbiologie
d I f k i bi l i
E‐mail: markus.nett@hki‐jena.de
Grundvorgänge der Massenspektrometrie
Ionisierung
Fragmentierung
MassenFokussierung
Zerfall in
geladene und ungeladene
Bruchstücke
Trennung der
gebildeten Bruchstücke
nach ihrer Masse
-2-
Wie werden organische Substanzen ionisiert?
durch Beschuss der Probenmoleküle mit Elektronen, Ionen oder Photonen
 Elektronenstoß-Ionisation
Elektronenstoß Ionisation (EI)
 Chemische Ionisation (CI)
 Fast-Atom-Bombardment (FAB)
 Matrix
Matrix-unterstützte
unterstützte Laserdesorptions
Laserdesorptions-Ionisation
Ionisation (MALDI)
durch elektrische Felder
 Elektrospray-Ionisation (ESI)
-3-
Elektronenstoß-Ionisation (EI)
Glühkathode
Elektronenstrahl
Hochvakuum
10-4 – 10-7 Torr
Spalte,
elektr. Linsensysteme
+
+
Vakuumschleuse
mit Probenheizung
+
+
+
+
+
positive Ionen
→ Massenanalysator
y
Elektronenauffänger
Hochvakuumpumpe
Beschuss mit energiereichen Elektronen (70 eV)
“harte” Ionisierung (Ionisierungspotential: 7-15 eV)
Spaltung chemischer Bindungen unter Bildung zahlreicher Fragmentionen
-4-
Chemische Ionisation (CI)
Glühk th d
Glühkathode
0,2 – 2 Torr
Elektronenstrahl (150 eV)
Probenmoleküle
Ionenstrom zum
Massenanalysator
Elektronenauffänger
Linsensystem der
Ionenquelle
Reaktandgas
Reaktandgas wird durch Elektronenbeschuss ionisiert
Protonenübertragung durch Zusammenstöße mit weiteren Reaktandgas-Molekülen
Reaktion mit dem gasförmigen Analyt unter Bildung von [M+H]+-Ionen
-5-
Chemische Ionisation – theoretische Grundlagen
Prinzip:
Ionisation erfolgt durch Ionenmolekülreaktion mit einem im Überschuß
zugesetzten Reaktandgas R, z.B. Methan, Isobutan, H2, NH3, ...
Primärreaktion:
Ionisation des Reaktandgases R mit hoher Energie (~150 eV)
R + e–
R+• + 2e–
(Ionisation)
R+• + R
RH+ + R •
(Protonierung)
Sekundärreaktionen: zwischen RH+ und dem Molekül M
RH+ + M
MH+ + R
(Protonierung)
[M+1]-Ion
RH+ + M
M-H+ + R + H2
((H-Abstraktion))
[M-1]-Ion
RH+ + M
MRH+
[M+RX]-Ion
-6-
(Anlagerung)
Fast-Atom-Bombardment (FAB)
Primärpartikel
(Ar, Xe)
Hochvakuum
Sekundärpartikel
Neutralteilchen,
Ionen, Elektronen
Selvedge
Region
Matrix
Analyt
Analyt in einer flüssigen, schwer flüchtigen Matrix
Beschuß mit 5-30 keV-Partikeln
Zerstäubung der Matrix, Stosskaskade, Bildung von Sekundärpartikeln
-7-
Matrix-unterstützte Laserdesorptions-Ionisation (MALDI)
Laserstrahl
Analyt-Ion
zum Massenanalysator
Matrix-Ion
Matrix/Analyt
Analyt in einer flüssigen Matrix
Ionisation mit einem gepulsten Laserstrahl
Beschleunigung der entstandenen Ionen in einem elektrischen Feld
-8-
Elektrospray-Ionisation (ESI) – Prinzip
Auslaß
Stickstoff:
nebulizer-gas
Atmosphärendruck
Gegenelektrode
–
Spraybildung
+
–
Kapillare
gelöste
Probe
Transferoptik
+
–
+
+
Spülgas
((bath-gas,
g
Stickstoff))
+
Mikroöffnung
(sample cone)
+
+
–
Ionen zum Hochvakuum
und Massenanalysator
+
–
Skimmer
2–6 kV
Zerstäubung der Probenlösung in einem elektrischen Feld
Verdampfung des Lösungsmittels => Coulomb-Explosion
Detektion von Quasi-Molekülionen, v.a. [M+H]+ und [M+Na]+ bzw. [M-H]–
-9-
Massenspektrum
Darstellung der Ionenhäufigkeit über das Masse-Ladungsverhältnis m/z,
normiert auf den Peak mit der größten Häufigkeit (Basispeak: I = 100%)
Basispeak
Fragmentpeaks
75 eV-EI-MS von Myrcen
41
93
69
+
Molpeak M •
136
- 10 -
m/z
rel. Intensität
41
69
93
136
100 %
78 %
94 %
6%
Identifizierung des Molpeaks in EI-MS-Spektren
 meist die höchste auftretende Massenzahl
 Peak kann sehr geringe Intensität aufweisen (Fragmentierung)
Abnahme der Intensität des Molpeaks
- 11 -
Identifizierung des Molpeaks in EI-MS-Spektren
Plausible Massendifferenzen zu den nächsten Signalen?
Δ4 - 14 sowie Δ21 - 25 zwischen Molpeak und erstem Fragmentpeak sind unwahrscheinlich.
Der Molpeak ist immer ein Radikalkation M+•
ungerade Elektronenzahl (OE+• , odd electron)
I mitit einer
Ion
i
geraden
d Elektronenzahl
El kt
hl (EE+, even electron)
l t )
C - Atome -
F
Fragmentpeak
t
k
H - Atome N - Atome

1
2
2
ja
OE+•
nein
EE+
Ergebnis gerade?
- 12 -
Identifizierung des Molpeaks – Übungsaufgabe
Durch peak matching wurde die Elementarzusammensetzung der
folgenden Ionen bestimmt. Welches Ion kommt als Molpeak in Betracht?
I #1
Ion
#1:
C10H14O
Ion #2:
C6H8NO2
- 13 -
Informationen aus dem Signal des Molpeaks
 Summenformel
 Stickstoffregel
• Eine ungerade Massenzahl des Molekülions weist auf das Vorhandensein einer
ungeraden Zahl von N-Atomen im Molekül hin.
• Ist die Massenzahl dagegen geradzahlig, enthält das Molekül entweder gar keinen
Stickstoff oder eine gerade Zahl von N-Atomen
N Atomen.
 Isotopenmuster
Hinweis auf das Vorkommen von Cl,
Cl Br,
Br Ni,
Ni Cu
Cu, Zn
Zn, etc
etc.
- 14 -
Hochauflösende Massenspektrometrie
Mit Ausnahme des Kohlenstoffisotops 12C sind die Atommassen der
Elemente nicht ganzzahlig.
1
14
16
=> Massendefekt
H hat eine Atommasse von
1.007825 u
N hat eine Atommasse von 14.003074
14 003074 u
O hat eine Atommasse von 15.994915 u
Wenn die Massenzahl eines Ions auf mindestens vier Dezimalstellen
genau bestimmt werden kann,, so läßt sich dessen monoisotopische
g
p
elementare Zusammensetzung berechnen.
Bestimmung der Summenformel
- 15 -
Peak-matching-Methode
Die experimentell bestimmte Masse wird mit der exakten Masse einer
Referenzsubstanz verglichen.
In dem folgenden Beispiel wurde die Masse des Molekülions mit 566,2179 u bestimmt:
- 16 -
Abschätzen der Summenformel mit der „Rule of 13“
1
Abstraktion: das Molekül besteht nur aus C- und H-Atomen;
die Zahl 13 entspricht der Summe der Atommassen eines C- und eines H-Atoms
M: Molekulargewicht
M/13 = n + r/13
/13
n: ganzzahliger Anteil
r:
Summenformel:
Rest
CnHn+r
Der Grad der Ungesättigtheit, d.h. die Anzahl der Doppelbindungen und/oder Ringe in
dem potentiellen Molekül, berechnet sich nach der Formel:
DBE = (n – r + 2)/2
J. Chem. Educ. 1983, 60, 557-558
- 17 -
„Rule of 13“ – Übungsaufgabe 1
Bestimmen Sie die Summenformel und den Grad an Ungesättigtheit für
ein Molekülion mit der Masse 78. Um was für eine Verbindung könnte
es sich handeln?
- 18 -
Abschätzen der Summenformel mit der „Rule of 13“
2
Für die Erweiterung der Summenformel CnHn+r um andere Elemente muss zunächst das
CH-Massenäquivalent subtrahiert werden.
Element
CH-Äquivalent
N
CH2
O
CH4
F
CH7
P
C2H7
S
C2H8
35
Cl
C2H11
79
Br
C6H7 od. C5H19
I
DBE =
2C + 2 – H + j Σ(B – 2)
2
C: Anzahl C-Atome in der erweiterten Summenformel
H: Anzahl H-Atome in der erweiterten Summenformel
j:
Anzahl der eingeführten Atome
B: Anzahl der Bindungen, die das eingeführte Atom eingeht
C10H7
J. Chem. Educ. 1983, 60, 557-558
- 19 -
„Rule of 13“ – Übungsaufgabe 2
Bestimmen Sie die Summenformel und den Grad an Ungesättigtheit für
ein Molekülion mit der Masse 142, das entweder (i) ein Sauerstoffatom
oder (ii) ein Chloratom enthält.
- 20 -
„Rule of 13“ – Übungsaufgabe 3
Sie erhalten EI-MS- und IR-Spektrum
einer nicht identifizierten Verbindung.
Machen Sie einen Vorschlag zu der
Summenformel des betreffenden
Moleküls nach Auswertung der Spektren.
Um was für eine Verbindung könnte es
sich handeln?
4000
3000
- 21 -
2000
1500
1000
500
Doppelbindungsäquivalente (DBE)
Berechnung Doppelbindungsäquivalente
1. O- und S-Atome in der Summenformel ersatzlos streichen
2. jedes Halogen durch ein H-Atom ersetzen
3. für jedes N- und/oder P-Atom die Anzahl der H-Atome um 1 reduzieren
(2 x n + 2) – m
DBE =
2
jede Doppelbindung
=
1 DBE
jeder Ring
=
1 DBE
jede Dreifachbindung
=
2 DBE
z.B. C=C, C=O, C=N, C=S, N=O, N=N, S=O
z.B. C≡C, C≡N
- 22 -
n: Anzahl der C-Atome
m: Anzahl der H-Atome
Doppelbindungsäquivalente (DBE) – Anwendungsbeispiele
Im Falle eines gesättigten, acyclischen Kohlenwasserstoffs gilt:
m = 2 x n +2
(2 x n +2) – (2 x n + 2)
DBE =
=0
2
Verbindung
Summenformel
Anzahl
Doppelbindungen
Anzahl
Ringe
C6H6
3
1
(2 x 6 +2)
2) – 6
2
=4
Essigsäure
C2H4O2
1
0
(2 x 2 +2) – 4
2
=1
Ethanol
C2H6O
0
0
(2 x 2 +2) – 6
2
=0
C2H5NO2
1
0
(2 x 2 +2) – 4
2
=1
C8H10O2N4
4
(2 x 8 +2) – 6
2
=6
Benzen
Glycin
Coffein
- 23 -
2
DBE
Übungsaufgabe 4
Berechnen Sie die Doppelbindungsäquivalente für die folgenden
Summenformeln und machen Sie Vorschläge zu den Strukturen der
jeweiligen Verbindungen!
1)
C5H5N
2))
C10H8
3)
C3H4O4
4)
C3H5NO
- 24 -
Isotopenmuster
Die natürlich vorkommenden Elemente sind häufig Mischungen aus mehreren Isotopen des
gleichen Elements, z.B. 12C/13C (98.90/1.10); 35Cl/37Cl (75.43/24.57); 79Br/81Br (50.44/49.56)
In der Massenspektrometrie werden die einzelnen Isotope eines Moleküls getrennt registriert.
Isotopenpeaks Die durch Kombination mit den schwereren Isotopen gebildeten Molekülionen
liegen bei entsprechend höheren MZ und werden bezeichnet: M+1, M+2, ...
Beispiel:
CH3Cl
MZ
12
C1H335Cl
50
M+•
13
C1H335Cl
51
M+1
(12C2H1H235Cl)
51
M+1
12
52
M+2
52
M+2
C1H337Cl
(13C2H1H235Cl)
- 25 -
sehr geringe Wahrscheinlichkeit
sehr geringe Wahrscheinlichkeit
Isotopenmuster
+
Molpeak M •
75 eV-EI-MS von m-Dichlorbenzen
m/z
rel. Intensität
146
147
148
149
150
100 %
7%
63 %
4%
10 %
146
148
Fragmentpeaks
111
75
50
150
- 26 -
Isotopenpeaks
Fragmentierungsreaktionen in der EI
EI--MS
Spaltung einer chem. Bindung
Spaltung zweier Bindungen
Folgespaltungen
• Alkylspaltung
• Retro-Diels-Alder-Reaktion
• Olefinspaltung
• Abspaltung von CO
• Allylspaltung
• Benzyl-/Tropyliumspaltung
• α-Spaltung
Umlagerungen
• McLafferty-Umlagerung
- 27 -
• Onium-Umlagerung
Fragmentierung bei der EI-MS
–e•
–e•
–e•
–e•
–e•
Molekül
Ionisierung
+
•
Molekülion
+
•
NeutralN
t l
molekül
RadikalR
dik l
Kation
+
•
Neutralmolekül
•
RadikalKation
Radikal
•
Radikal
+
Kation
+
Kation
+
Neutralmolekül
Kation
Stephenson-Audier-Regel
Die Ladung wird von dem Bruchstück mit dem kleineren Ionisierungspotential übernommen,
d.h. von jenem Fragment, das am leichtesten ein Elektron abgeben könnte.
Heteroaromaten,
Aromaten
und
konjugierte Polyene besitzen relativ
niedrige Ionisierungspotentiale.
- 29 -
Fragmentierungsreaktionen – allgemeine Prinzipien
Fragmentierungs-Reaktionen in der EI-MS sind
 monomolekular
 endotherm
 kinetisch kontrolliert
Welche Bindung gespalten wird, hängt ab von
 der Bindungsenergie
 der Stabilität der gebildeten Fragmente
? Neutralmoleküle
? durch induktive Effekte, Mesomerie oder Umlagerung stabilisierbare Kationen
- 30 -
Alkylspaltung (σ-Spaltung)
• Spaltung erfolgt an verzweigten C-Atomen
• Präferenz für den Verlust des größten Alkylradikals
Stabilisierung des CarboCarbo-Kations durch induktive Effekte
+
+
+
+
CH3 < RCH2 < R2CH < R3C
CH3
+
•
CH3
– CH2 – CH•2
– CH2 – CH2 – C –
+ +C –
CH3
CH3
- 31 -
Alkylspaltung (σ-Spaltung)
CH3
H3C – CH – CH2 – CH2 – CH2 – CH3
43
43
85
+
Molpeak M •
100
Übungsaufgabe 5
Ordnen Sie die den nachfolgenden
43
Stellungsisomeren (C8H18) die
zugehörigen MS-Spektren zu:
85
29
57
3-Ethylhexan
114
71
57
2,2-Dimethylhexan
29
99
- 33 -
Allylspaltung
Spaltung erfolgt in Allylstellung
Stabilisierung
g des CarboCarbo-Kations durch mesomere Effekte
– CH = CH – CH2 – CH2 –
– CH = CH – CH2+
+
•
–+CH – CH = CH2
- 34 -
+ • CH –
2
Allylspaltung
CH3
H3C – C = CH – CH2 – CH2 – CH3
69
69
+
Molpeak M •
98
Benzyl- oder Tropyliumspaltung
Spaltung erfolgt in der Benzylstellung
Stabilisierung
g durch Umlagerung
g
g zum TropyliumTropylium
py
-Kation
+
•
X•
– CH2 – X
+
– CH2+
Umlagerung
+
- 36 -
Benzyl- oder Tropyliumspaltung
BenzylSpaltung
+
+
+
C3H7•
+
H2C = CH – CH3
m/z 91
C6H5 – C4H9 •
m/z 134
C6H5 – CH2
+
McLaffertyUmlagerung
C6H5 – CH3 •
m/z 92
91
92
+
Molpeak M •
134
α-Spaltung
Bei einfach gebundenen Heteroatomen (O, S, N) wird bevorzugt die α-Bindung
gespalten, weil das entstehende Kation durch Mesomerie stabilisiert wird.
Der schwerere Substituent wird bevorzugt eliminiert.
R – X – CH2 – R´
–
R – X – CH2+
+
+
•
R – X = CH2
- 38 -
+ • R´
α-Spaltung
H
58
H3C – CH2 – N – CH2 – CH2 – CH3
72
58
+
Molpeak M •
87
72
α-Spaltung
• Spaltung erfolgt an der zur Carbonylfunktion benachbarten Bindung
Stabilisierung des CarboCarbo-Kations durch mesomere Effekte
• bevorzugte Eliminierung des größeren Radikals
• Säure < Ester < Keton
=
R – CH2 – C – R´
+
•
O
+
+
O
- 40 -
C – R´
≡
C – R´
=
R – CH2•
+O
α-Spaltung
57
H3C – CH2 – C – CH2 – CH2 – CH2 – CH2 – CH3
=
O
99
57
99
+
Molpeak M •
128
Retro-Diels-Alder-Reaktion (RDA-Reaktion)
• Sechsgliedrige cyclische Systeme, die eine Doppelbindung enthalten, zerfallen in
eine Dien- und eine En-Komponente.
• Ladung verbleibt i.d.R. am Dien
• alternative Ladungsverteilung?
Detektion der En-Komponente im MS
+
•
+
•
+
- 42 -
Retro-Diels-Alder-Reaktion (RDA-Reaktion)
+
•
+
•
+
m/z 68
m/z 136
68
+
Molpeak M •
136
McLafferty-Umlagerung
• Übertragung des γ-ständigen H-Atoms auf ein doppelt gebundenes Atom X
• X ist meistens ein Heteroatom
• Verschiebung der Doppelbindung
• Eliminierung eines Neutralteilchens mit den β- und γ-ständigen Atomen
+•
+• H
X
α
γ
β
H
γ
X
+
α
- 44 -
β
McLafferty-Umlagerung
γ
β
α
+
H2C = C (OH)2•
=
H3C – CH2 – CH2 – CH2 – C – OH
H3C – CH = CH2
+
•
m/z 102
O
m/z 60
60
Folgespaltungen
Die bei der Alkylspaltung entstandenen Kationen können durch Eliminierung
von Olefinen weiter fragmentieren (Olefinspaltung):
+
R – CH2+
R – CH2 – CH2 – C
+
H2C = C
Aus den durch α-Spaltung gebildeten Kationen wird leicht CO eliminiert
(CO-Verlust):
+
C–R
CO
O
- 46 -
+
R+
CO-Verlust
+
•
OH
m/z 94
+
•
O
m/z 66
+
CO
+
Molpeak M •
94
66
Folgespaltungen
Die bei der α-Spaltung gebildeten Onium-Ionen können einer Umlagerung
unterliegen (Onium-Umlagerung):
R – CH2 – CH2 – CH2 – X = C
+
R – CH2 – CH = CH2
+
H–X=C
+
- 48 -
Übungsaufgabe 6
Erläutern Sie die Fragmentierung der abgebildeten Verbindung bei der EI-MS.
205
220
57
- 49 -
Übungsaufgabe 7
Erläutern Sie die Fragmentierung der abgebildeten Verbindung bei der EI-MS.
- 50 -
Übungsaufgabe 8
Erläutern Sie die Fragmentierung der abgebildeten Verbindung bei der EI-MS.
41
93
69
+
M•
136
- 51 -
Übungsaufgabe 9
Erläutern Sie die Fragmentierung der abgebildeten Verbindung bei der EI-MS.
m/z
- 52 -
Übungsaufgabe 10
Interpretieren Sie das dargestellte MS-Spektrum im Hinblick auf
• charakteristische (M – X)-Signale
• Schlüsselbruchstücke und Serien
• stattgefundene Fragmentierungen
Arecolin
140
96
155
53
124