Trigonometrie Sinus und Kosinus - Mathe

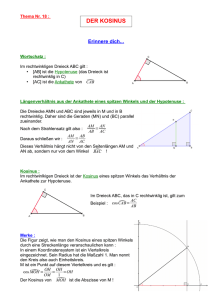
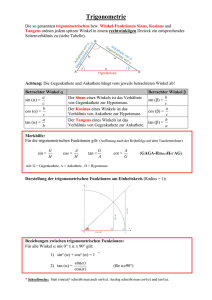
Trigonometrie
Sinus und Kosinus
© www.mathe-video.com
Sinus im rechtwinkligen Dreieck
Länge der Gegenkathete von (Winkel)
sin(Winkel) =
Länge der Hypotenuse
Hier gilt:
α
a
sin α =
c
© www.mathe-video.com
Sinus im rechtwinkligen
Dreieck
Länge der Gegenkathete von (Winkel)
sin(Winkel) =
Länge der Hypotenuse
Hier gilt:
d
sin δ =
e
δ
© www.mathe-video.com
Sinus im rechtwinkligen
Dreieck
Länge der Gegenkathete von (Winkel)
sin(Winkel) =
Länge der Hypotenuse
ϕ
Hier gilt:
sinϕ=?
f
sin ϕ =
e
© www.mathe-video.com
Sinuswert mit GTR
bestimmen
Länge der Gegenkathete von (Winkel)
sin(Winkel) =
Länge der Hypotenuse
sin 45° = (GTR) = 0,71
sin 60° = 0,87
(Pause)
sin70° = ? = 0,94
sin81° = ? = 0,99
sin31° = ? = 0,52
© www.mathe-video.com
Winkelmaß mit GTR
bestimmen
sin α = 0,4
| sin−1
−1
α = sin 0,4 = 23,58°
(Pause)
sin α 2 = 0,2
α 2 = 11,54°
sin α 3 = 0,95
α 3 = 71,81°
sin α 4 = 0,46
α 4 = 27,39°
© www.mathe-video.com
Kosinus im rechtwinkligen
Dreieck
Länge der Ankathete von (Winkel)
cos(Winkel) =
Länge der Hypotenuse
Hier gilt:
b
cos α =
c
α
© www.mathe-video.com
Kosinus im rechtwinkligen
Dreieck
Länge der Ankathete von (Winkel)
cos(Winkel) =
Länge der Hypotenuse
Hier gilt:
f
cos δ =
e
δ
© www.mathe-video.com
Kosinus im rechtwinkligen
Dreieck
Länge der Ankathete von (Winkel)
cos(Winkel) =
Länge der Hypotenuse
ϕ
Hier gilt:
cosϕ=?
d
cos ϕ =
e
© www.mathe-video.com
Kosinuswert mit GTR
berechnen
Länge der Ankathete von α
cos α =
Länge der Hypotenuse
cos 45° = (GTR) = 0,71
cos 60° = 0,5
(Pause)
cos70° = ? = 0,34
cos81° = ? = 0,16
cos36° = ? = 0,81
© www.mathe-video.com
Winkelmaß mit GTR
bestimmen
cos α = 0,55
| cos−1
−1
α = cos 0,55 = 66,42°
(Pause)
cos α 2 = 0,2
α 2 = 78,46°
cos α 3 = 0,95 α 3 = 18,19°
cos α 4 = 0,46 α 4 = 62,61°
© www.mathe-video.com
Beispielaufgabe
geg : Dreieck ABC mit a = 9 cm c = 7 cm und α = 90°
Berechne β, γ und b!
c 7cm 7
cos β = =
=
a 9cm 9
−1  7 
β = cos   = 38,94°
9
γ
β
γ = 180° − 90° - 38,94°
γ = 51,06°
© www.mathe-video.com
Beispielaufgabe
geg : Dreieck ABC mit a = 9 cm c = 7 cm und α = 90°
Berechne β, γ und b!
b berechnen:
γ
b
sin β =
a
β
b = sin38,94° ⋅ 9 cm
b = 5,66 cm
© www.mathe-video.com
Übungsaufgabe
geg : Dreieck ABC mit a = 8 cm c = 6 cm und α = 90°
Berechne β, γ und b!
γ
(Pause)
β
c 6cm 6
cos β = =
=
a 8cm 8
−1  6 
β = cos   = 41,41°
8
γ = 180° − 90° - 41,41°
γ = 48,59°
© www.mathe-video.com
Beispielaufgabe
geg : Dreieck ABC mit a = 8 cm c = 6 cm und α = 90°
Berechne β, γ und b!
b berechnen:
γ
b
sin β =
a
β
b = sin 41,41° ⋅ 8 cm
b = 5,29 cm
© www.mathe-video.com
Weitere Aufgaben und Lösungen
zu diesem Thema und zu
vielen anderen Themen:
www.mathe-video.com
© www.mathe-video.com