Viereck und Winkelhalbierende

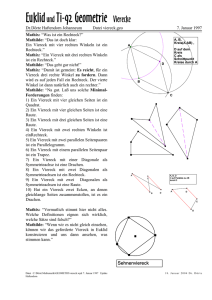
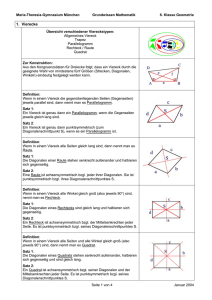
Viereck und Winkelhalbierende
oder, ... ein Viereck kommt selten allein
Konstruiert man bei einem Dreieck die 3 Winkelhalbierenden, so verlaufen diese bekanntlich durch einen Punkt W
und W ist der Mittelpunkt des Innenkreises des Dreiecks.
1.
Bei speziellen Vierecken verlaufen die 4 Winkelhalbierenden auch durch einen Punkt und dieser Punkt ist
dann der Mittelpunkt eines Innenkreises.
Gib begründet eine Bedingung an, die ein Viereck
erfüllen muss, damit die 4 Winkelhalbierenden durch
einen Punkt verlaufen. Nenne spezielle Vierecke aus
“dem Haus der Vierecke”, die diese Bedingung erfüllen.
Im Allgemeinen verlaufen die vier Winkelhalbierenden eines Viereckes nicht durch einen
Punkt, sondern sie schneiden sich paarweise in
vier neuen Punkten, die wiederum ein Viereck
bilden.
2.
Zeichne in dein Heft ein beliebiges Viereck (die Spezialfälle der Aufgabe 1 vermeiden) und konstruiere das Viereck, gebildet aus den 4 Schnittpunkten der Winkelhalbierenden. Bezeichne die Elemente
deiner Figur so wie in der nebenstehenden
Skizze und untersuche das neue Viereck
~EFGH auf Besonderheiten. - Schon etwas entdeckt? - Vergleiche mit den Ergebnissen der Nachbarn.
Bei mir sieht es so aus, als besäße das Viereck
einen Außenkreis. Ist es bei deiner Konstruktion und bei der deiner Nachbarn auch so?
3.
Gib begründet eine Bedingung an, die ein
Viereck erfüllen muss, damit alle 4 Punkte auf einem Kreis liegen, d.h. welcher
Bedingung genügt ein Sehnenviereck eines Kreises? - Nenne spezielle Vierecke
aus “dem Haus der Vierecke”, die diese
Bedingung erfüllen.
Viereck und Winkelhalbierende
oder, ... ein Viereck kommt selten allein
4.
Benenne in deiner Skizze die Winkel:
ËDHA ': ε
ËBFC ': n
und beweise: ε % n ' 180E .
Tipp:
Verwende den Winkelsummensatz in
den Dreiecken ∆AHD und ∆BCF.
5.
Beweise:
Im Viereck ~EFGH gilt: Die Summe der
Winkelmaße zweier gegenüber liegender
Winkel ist 180E, womit das Viereck ein
Sehnenviereck ist.
6.
(Hausaufgabe):
Untersuche den Spezialfall, dass das Ausgangsviereck ~ABCD ein Parallelogramm ist; welche
Auswirkungen hat dies für das Viereck ~EFGH, gebildet aus den paarweisen Schnittpunkten der
Winkelhalbierenden. Formuliere einen entsprechenden Satz in der Form: “Wenn ein Viereck ein
Parallelogramm ist, dann .... “. Beweise deine Behauptung.
Kennst du weitere Spezialfälle? - Könnte das Viereck ~EFGH ein Quadrat sein?
7.
In der nebenstehenden Skizze wurden an die Vierecksseiten des Vierecks ~ABCD die Ankreise konstruiert. Die Mittelpunkte E, F, G, H dieser Ankreise bilden ein neues Viereck.
Beweise:
Im Viereck ~EFGH gilt: Die Summe
der Winkelmaße zweier gegenüber
liegender Winkel ist 180E, womit das
Viereck ein Sehnenviereck ist.
Überlege:
Wie konstruiert man eigentlich die Mittelpunkte der Ankreise? - Was folgt aus den eingezeichneten Berührbedingungen?