Zusammenfassung: Elektromagnetische Schwingungen und Wellen

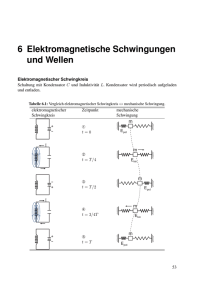
LGÖ Ks
Ph 13 4-stündig
21.11.2011
Zusammenfassung: Elektromagnetische Schwingungen und Wellen
Elektromagnetische Schwingungen
Ein elektromagnetischer Schwingkreis besteht aus einem Kondensator
und einer Spule. In der gezeichneten Schalterstellung wird der
I
Kondensator aufgeladen. Nach Umlegen des Schalters beginnt der
Kondensator, sich über die Spule zu entladen. Die Selbstinduktion der
Spule wirkt dem Stromstärkeanstieg entgegen, so dass sich der
U0
U
Kondensator nicht schlagartig entlädt. Die Stromstärke ist am größten,
wenn der Kondensator gerade entladen ist. Nun bewirkt die Selbstinduktion der Spule, dass der Strom weiterfließt. Dadurch lädt sich der
Kondensator mit umgekehrtem Vorzeichen wieder auf. Betrachtet man die Spule als ideal, so dass
keine Energie verloren geht, dann liegt schließlich am Kondensator wieder dieselbe Spannung wie zu
Beginn, nur mit umgekehrtem Vorzeichen. Nun wiederholt sich der ganze Vorgang mit umgekehrtem Vorzeichen, bis wieder der Ausgangszustand erreicht ist.
Bei einer solchen elektromagnetischen Schwingung pendelt die Energie periodisch zwischen dem
elektrischen Feld des Kondensators und dem Magnetfeld der Spule hin und her.
Wir betrachten einen Schwingkreis aus einem Kondensator der
Kapazität C und einer Spule der Induktivität L. Ist U die maximale
Spannung und I die maximale Stromstärke, dann gilt für eine
ungedämpfte Schwingung der Energieerhaltungssatz:
Wel = Wmag
I
U
C
L
2
1
1 2
CU = LI .
2
2
Wir leiten die Differenzialgleichung einer ungedämpften elektromagnetischen Schwingung her:
Die Spannung an der Spule, also die Induktionsspannung U ind ( t ) , ist gleich der Spannung U C ( t ) am
Kondensator:
Es ist C =
U ind ( t ) = U C ( t )
•
Q (t )
U
Q
, also U C ( t ) =
, und L = − •ind , also U ind ( t ) = − L ⋅ I ( t ) :
U
C
I
•
−L ⋅ I (t ) =
Q (t )
C
1
I (t ) = −
⋅ Q (t ).
LC
•
•
•
••
Stets gilt I ( t ) = Q ( t ) , also I ( t ) = Q ( t ) . Einsetzen ergibt die Differenzialgleichung einer
ungedämpften elektromagnetischen Schwingung:
••
Q (t ) = −
10b_zus_elektromagnetischeschwingungenundwellen 1/8
1
⋅ Q (t ) .
LC
LGÖ Ks
Ph 13 4-stündig
21.11.2011
Diese DGL ist analog zur DGL einer mechanischen Schwingung. Entsprechend ist die Lösung der
DGL die (von der maximalen Ladung Q und dem Phasenwinkel ϕ abhängende) Funktion
Q ( t ) = Q ⋅ sin (ω t + ϕ ) .
Zweimaliges Ableiten dieser Funktion ergibt
•
Q ( t ) = ω Q ⋅ cos (ω t + ϕ )
••
Q ( t ) = −ω 2 Q ⋅ sin (ω t + ϕ ) = −ω 2 ⋅ Q ( t ) ,
und Einsetzen in die DGL ergibt
1
−ω 2 ⋅ Q ( t ) = −
⋅ Q (t )
LC
1
ω2 =
LC
1
ω=
.
LC
2π
Wegen ω =
folgt daraus die
T
Thomson’sche Schwingungsgleichung: Ein ungedämpfter Schwingkreis aus
einem Kondensator der Kapazität C und einer Spule der Induktivität L
schwingt mit der Periodendauer
T = 2π LC .
C
L
Üblicherweise wird der Kondensator zunächst auf eine Spannung U 0 aufgeladen und von der
Spannungsquelle getrennt. Dann ist die maximale Spannung U = U 0 . Die maximale Ladung Q
Q
berechnet man aus der Beziehung C = , und die maximale Stromstärke I berechnet man aus der
U
2
2
1
1
Beziehung CU = LI (siehe oben). Wird der Kondensator zum Zeitpunkt t = 0 mit der Spule
2
2
verbunden, dann gilt
U ( t ) = U ⋅ cos (ω t )
Q ( t ) = C ⋅ U ( t ) = CU ⋅ cos (ω t ) = Q ⋅ cos (ω t )
•
I ( t ) = Q ( t ) = −ω Q ⋅ sin (ω t ) = − I ⋅ sin (ω t ) .
Häufig rechnet man die Stromstärke mit umgekehrtem Vorzeichen, also
I ( t ) = I ⋅ sin (ω t ) .
Einschub: Transistor
C
D
Ein bipolarer Transistor hat drei Anschlüsse:
B
Basis (B), Kollektor (C) und Emitter (E).
G
Ein Feldeffekttransistor hat die entsprechenden Anschlüsse:
E
S
Gate (G), Drain (D) und Source (S).
Wir zeichnen im Folgenden einen bipolaren Transistor; man kann aber genauso gut einen Feldeffekttransistor verwenden.
10b_zus_elektromagnetischeschwingungenundwellen 2/8
LGÖ Ks
Ph 13 4-stündig
21.11.2011
IC
Mit nebenstehender Schaltung
erhält man die Kennlinie eines
I
Transistors, also die AbhängigU0
keit der Stromstärke I C der
Kollektor-Emitter-Strecke von
U
der Spannung U BE zwischen
U Schw
U BE
Basis und Emitter.
Ab der sog. Schwellspannung U Schw wird der Transistor leitend. Die Schwellspannung ist bei einem
bipolaren Transistor ungefähr 0,7 V und bei einem Feldeffekttransistor ungefähr 3 V.
Meißner-Schaltung zur Erzeugung ungedämpfter Schwingungen:
Stelle mit dem Potentiometer den Arbeitspunkt des
Transistors ein, d. h. eine Spannung knapp unterhalb der
Schwellspannung.
Die Schwingkreisspule ist über einen Eisenkern mit einer
Induktionsspule gekoppelt. Wird in der Induktionsspule
eine Spannung mit der eingezeichneten Polarität induziert,
dann wird der Transistor leitend. Dadurch wird das
U0
Aufladen des Kondensators unterstützt, und dem
Schwingkreis wird Energie zugeführt.
Der Transistor wird also nach dem Prinzip der
Rückkopplung gesteuert, d. h. der Schwingkreis steuert
selbst den Zeitpunkt, zu dem der Transistor leitend wird.
Der Widerstand dient zur Strombegrenzung bei der Aufladung des Kondensators.
Elektromagnetische Wellen
1. Hertz’scher Dipol
Denkt man sich bei einem Schwingkreis die Kondensatorplatten auseinander gebogen und jeweils zu
einem Stück Draht entartet und denkt man sich die Spule zu einem geraden Draht auseinander
gezogen, dann erhält man ein gerades Stück Draht. Ein solcher Hertz’scher Dipol ist zu elektromagnetischen Schwingungen fähig: Koppelt man einen Hertz’schen Dipol an einen hochfrequenten
Schwingkreis, dann entsteht in der Umgebung des Dipols ein sich änderndes elektrisches Feld (am
stärksten in der Umgebung der Dipolenden) und ein sich änderndes Magnetfeld (am stärksten in der
Umgebung der Dipolmitte):
3
T
T
t= T:
t= :
t= :
t = 0:
4
4
2
E
I
B
E
I
B
2. Ausbreitung elektromagnetischer Wellen
Aus dem Kapitel „Induktion“ ist bekannt:
Ein sich änderndes Magnetfeld erzeugt ein elektrisches Wirbelfeld, d. h. die elektrischen Feldlinien
verlaufen kreisförmig um die Magnetfeldlinien.
10b_zus_elektromagnetischeschwingungenundwellen 3/8
LGÖ Ks
Ph 13 4-stündig
Nebenstehend ist ein anwachsendes
Magnetfeld dargestellt.
Die Richtung der elektrischen Feldlinien
bestimmt man mit der Lenzschen Regel.
21.11.2011
B
E
Ohne Begründung: Es gilt auch die „Umkehrung“:
Ein sich änderndes elektrisches Feld erzeugt ein magnetisches Wirbelfeld, d. h. die magnetischen
Feldlinien verlaufen kreisförmig um die elektrischen Feldlinien.
Nebenstehend ist ein anwachsendes
elektrisches Feld dargestellt.
Die Richtung der Magnetfeldlinien soll
hier nicht begründet werden.
E
B
Betrachte das von einem schwingenden Hertz’schen Dipol erzeugte sich ändernde elektrische Feld.
Es erzeugt ein sich änderndes Magnetfeld. Dieses erzeugt wiederum ein sich änderndes elektrisches
Feld usw.: eine elektromagnetische Welle breitet sich aus.
Man zeigt experimentell, dass elektromagnetische Wellen Transversalwellen sind, d. h. die elektrischen und die magnetischen Feldlinien verlaufen orthogonal zur Ausbreitungsrichtung (und sind
orthogonal zueinander).
Wie jede fortschreitende Welle transportiert eine elektromagnetische Welle Energie.
3. Ausbreitungsgeschwindigkeit einer elektromagnetischen Welle
Trifft eine elektromagnetische Welle auf eine Metallwand, dann wird sie (zu einem erheblichen Teil)
reflektiert, und vor der Wand bildet sich eine stehende Welle, wobei an der Wand ein Knoten der
elektrischen Feldstärke ist. Hat die Welle die Wellenlänge λ, dann haben (wie bei jeder stehenden
λ
. Durch Ausmessen der Abstände der Knoten der
2
elektrischen Feldstärke kann man also experimentell die Wellenlänge einer elektromagnetischen
Welle bestimmen. Kennt man die Frequenz f der Welle, dann kann man ihre Ausbreitungsgeschwindigkeit c berechnen.
Welle) zwei benachbarte Knoten den Abstand
Herleitung siehe „Für Experten“: In einem Stoff der Dielektrizitätszahl ε r und der Permeabilitätszahl
µ r breitet sich eine elektromagnetische Welle mit der Geschwindigkeit
1
c=
ε 0 ε r µ0 µ r
aus. In Vakuum (und näherungsweise in Luft) ist ε r = µ r = 1 , also
c = c0 =
1
ε 0 µ0
1
=
≈ 2,99792 ⋅ 108
m
.
s
F
Vs
⋅ 4π ⋅ 10−7
m
Am
Also breitet sich eine elektromagnetische Welle im Vakuum mit der (Vakuum-)Lichtgeschwindigkeit
m
km
c0 ≈ 3, 00 ⋅ 108
= 300 000
s
s
aus.
8,85419 ⋅ 10−12
10b_zus_elektromagnetischeschwingungenundwellen 4/8
LGÖ Ks
Ph 13 4-stündig
21.11.2011
4. Resonanzbedingung bei einem Hertz’schen Dipol
An einem schwingenden Hertz’schen Dipol läuft eine elektromagnetische Welle entlang, die an den
Enden des Dipols reflektiert wird. Der Dipol schwingt nur kräftig, wenn sich dabei eine stehende
Welle bildet. An den Dipolenden
• häufen sich die elektrischen Ladungen am stärksten an; das elektrische Feld hat dort einen
Bauch;
• ist die Stromstärke Null, also auch die magnetische Flussdichte; das Magnetfeld hat dort
einen Knoten.
Dies sind die Randbedingungen eines beidseitig begrenzten Wellenträgers mit zwei festen bzw. mit
zwei freien Enden. Also tritt bei der Wellenlänge λ nur Resonanz auf, wenn für die Länge l des
Hertz’schen Dipols gilt:
l =k⋅
λ
2
Die kürzeste mögliche Dipollänge ist also l =
( k = 1; 2; 3; …).
λ
2
.
5. Elektromagnetische Wellen in Materie
Eine elektromagnetische Welle breitet sich
1
in Vakuum mit der (Vakuum-)Lichtgeschwindigkeit c0 =
•
in einem Stoff der Dielektrizitätszahl ε r und der Permeabilitätszahl µ r mit der Geschwindig1
aus.
keit c* =
ε 0 µ0
= 3, 00 ⋅ 108
m
aus;
s
•
ε 0ε r µ0 µr
Für alle nicht ferromagnetischen Stoffe (also alle Stoffe außer Eisen, Nickel und Kobalt) ist µ r ≈ 1 .
In solchen Stoffen gilt in guter Näherung
c
c* = 0 .
εr
Definition: Die Brechungszahl n eines Stoffs ist
n=
c0
.
c*
c0
, und für Stoffe mit µ r ≈ 1 ist n = ε r .
n
Beim Übergang einer elektromagnetischen Welle von Vakuum in einen Stoff der Brechungszahl n
bleibt die Frequenz gleich; also ändert sich die Wellenlänge. In Vakuum ist c0 = λ0 f , und in dem
Also ist c* =
Stoff ist c* = λ * f . Daraus folgt (dividiere die erste Gleichung durch die zweite Gleichung und
vertausche im Ergebnis die Seiten):
λ0 c0
= .
λ * c*
Die rechte Seite der Gleichung ist nach Definition die Brechungszahl n; also gilt
λ0
=n.
λ*
Merke: Die Wellenlängen verhalten sich wie die Ausbreitungsgeschwindigkeiten.
Stets ist ε r ≥ 1 , also n ≥ 1 , also c ≤ c0 und λ * ≤ λ0 .
10b_zus_elektromagnetischeschwingungenundwellen 5/8
LGÖ Ks
Ph 13 4-stündig
21.11.2011
6. Polarisation
Eine elektromagnetische Welle (z. B. Licht) heißt linear polarisiert, wenn die elektrischen Feldlinien
längs eines Wellenstrahls immer in derselben Ebene liegen.
Beispiele:
• Von einem Hertz’schen Dipol erzeugte elektromagnetische Wellen sind linear polarisiert.
• Laserlicht ist linear polarisiert.
• Sonnenlicht ist unpolarisiert.
• Das Licht einer Glühlampe ist unpolarisiert.
Trifft eine elektromagnetische Welle auf einen Polarisator (z. B. Licht auf eine Polarisationsfolie),
dann wird nur die zur Durchlassrichtung des Polarisators parallele Komponente E des elektrischen
Felds E durchgelassen.
Die Intensität einer elektromagnetischen Welle (z. B. von Licht) ist proportional zum Quadrat des
maximalen Betrags der elektrischen Feldstärke.
7. Messung der Lichtgeschwindigkeit
Drehspiegelmethode nach Foucault:
Aufbau:
Endspiegel
Drehspiegel
Ein Laserstrahl fällt auf einen Drehspiegel D, läuft von
d
D
E
dort zum Endspiegel E, wo er in sich reflektiert wird,
trifft wieder auf den Drehspiegel D und wird in die
l
Laser
∆ϕ
s
Laseröffnung zurückreflektiert. Neben dem Laser ist
Schirm
ein Schirm angebracht.
Durchführung:
Der Drehspiegel wird in Rotation versetzt. Während der Laufzeit ∆t des Lichts von D nach E und
zurück hat sich der Drehspiegel um den Winkel ∆ϕ weitergedreht. Deshalb wird der vom Endspiegel kommende Laserstrahl nicht in die Laseröffnung zurückreflektiert, sondern trifft um eine
kleine Strecke s versetzt auf dem Schirm auf.
Auswertung:
Die Strecke s wird auf einer Millimeterskala abgelesen.
Den Winkel ∆ϕ , um den sich der Drehspiegel gedreht hat, erhält man aus der Strecke s auf dem
Schirm und der Entfernung l des Schirms vom Drehspiegel.
Die Drehfrequenz des Drehspiegels bestimmt man mit einem Stroboskop.
Die Laufzeit ∆t erhält man aus dem Drehwinkel ∆ϕ und der Drehfrequenz des Drehspiegels.
Ist d die Entfernung zwischen dem Drehspiegel und dem Endspiegel, dann ist die Licht2d
geschwindigkeit c =
.
∆t
Für Experten: Seit 1983 ist die Lichtgeschwindigkeit im SI-System eine Grundeinheit; sie ist
definiert als die Geschwindigkeit 299 792 458 m s . Dafür ist seither die Einheit Meter eine
abgeleitete Einheit. Streng genommen misst man also nicht die Lichtgeschwindigkeit, sondern die
Einheit Meter.
10b_zus_elektromagnetischeschwingungenundwellen 6/8
LGÖ Ks
Ph 13 4-stündig
21.11.2011
Vergleich: Mechanische Schwingungen und elektromagnetische Schwingungen
Elektromagnetische Schwingung
Mechanische Schwingung
Trägheit der Masse
••
s (t ) = −
D
⋅ s (t )
m
Masse m
(Richtgröße D)
s ( t ) = s ⋅ sin (ω t + ϕ )
ω=
Eigenschaft, die das „Durchschwingen“ bewirkt:
Selbstinduktion der Spule
Differenzialgleichung:
••
1
Q (t ) = −
⋅ Q (t )
LC
entsprechende Größen:
Induktivität L
1
(Kehrwert
der Kapazität)
C
Lösung der DGL:
Q ( t ) = Q ⋅ sin (ω t + ϕ )
Winkelgeschwindigkeit:
1
ω=
LC
D
m
Periodendauer:
T = 2π
m
D
T = 2π LC
Für Experten
Herleitung der Ausbreitungsgeschwindigkeit einer elektromagnetischen Welle:
Aus dem Kapitel „Induktion“ ist bekannt:
Bewegt sich ein Leiter der Länge d in einem Magnetfeld der Flussdichte B mit der Geschwindigkeit v ( d ⊥ B und v ⊥ d und v ⊥ B ), dann werden in dem Leiter Elektronen verschoben, und in
dem Leiter entsteht ein elektrisches Feld der Feldstärke E. Es stellt sich ein stationärer Zustand ein,
in dem die elektrische Kraft Fel auf ein Elektron gleich der Lorentzkraft FL ist; es gilt also
Fel = FL
eE = Bev
E = Bv
Betrachtet man diesen Vorgang im Bezugssystem des Leiters, dann bewegt sich das Magnetfeld der
Flussdichte B mit der Geschwindigkeit v; die elektrische Feldstärke E bleibt gleich.
Ohne weitere Begründung: Dies gilt auch ohne Vorhandensein eines Leiters:
Ein mit der Geschwindigkeit v über einen Punkt hinwegziehendes Magnetfeld der Flussdichte B
erzeugt dort ein elektrisches Feld der Feldstärke
E = Bv .
10b_zus_elektromagnetischeschwingungenundwellen 7/8
LGÖ Ks
Ph 13 4-stündig
21.11.2011
Nimmt man an, dass bei einer elektromagnetischen Welle die Energiedichte ρel des elektrischen
Felds gleich der Energiedichte ρ mag des Magnetfelds ist, dann kann man die Ausbreitungsgeschwindigkeit v in einem Stoff der Dielektrizitätszahl ε r und der Permeabilitätszahl µ r berechnen:
ρel = ρ mag
1
1
B2
ε 0ε r E 2 =
2
2µ 0 µ r
ε 0ε r ( Bv ) =
2
ε 0ε r v 2 =
v=
10b_zus_elektromagnetischeschwingungenundwellen 8/8
1
µ0 µr
B2
1
µ0 µr
1
ε 0ε r µ0 µr