Vorkurs Mathematik 2014

Dr. Mario Helm et al.
Institut für Numerische Mathematik und Optimierung
Fakultät für Mathematik und Informatik
Vorkurs Mathematik 2014
Winkelmessung
und trigonometrische Funktionen
6.-10.10.2014
1 Winkel und Winkelmessung
Winkel. . . Teil der Ebene, der von zwei Strahlen („Schenkeln“) mit
gleichem Anfangspunkt („Scheitel“) begrenzt wird
Winkelmessung. . . Quantitative Erfassung der „Öffnungweite“, d. h.
lediglich der relativen Lage der Strahlen zueinander
Vorkurs
TU Bergakademie Freiberg
1
Bogenmaß
Die Winkelmessung im Bogenmaß erfolgt unter Beachtung des
Drehsinns am Einheitskreis:
1
ϕ
ϕ
0
1
Die Größe des Winkels im Bogenmaß entspricht der Länge des
ausgeschnitten Bogens auf dem Einheitskreis. Der Vollkreis entspricht
einem Winkel von 2π (Umfang des Einheitskreises).
Einheit: Zur Identifikation als Winkel verwendet man mitunter den
Radiant: 1 rad= 1 m
m = 1. Mathematisch gesehen ist das verzichtbar.
Vorkurs
TU Bergakademie Freiberg
2
Gradmaß
Beim Gradmaß wird die Größe des Vollkreises auf 360◦ normiert.
Damit entspricht dem Winkel π im Bogenmaß die Gradangabe 180◦ .
Für beliebige Winkel gelten die Umrechnungsformeln
180
· Winkel in Radiant
π
π
Winkel in Radiant =
· Winkel in Grad
180
Winkel in Grad =
Wie groß ist der rechte Winkel (90◦ ) im Bogenmaß? Wieviel Grad
entspricht 1 rad?
Vorkurs
TU Bergakademie Freiberg
3
Winkelmesser mit Grad und Radiant
Prägen Sie sich einige Werte auch im Bogenmaß ein. Achten Sie beim
Rechnen mit Winkeln auf korrekte Taschenrechnereinstellung (◦ /rad).
Vorkurs
TU Bergakademie Freiberg
4
Bogenminuten und Bogensekunden
Im Zusammenhang mit der Gradskala sind neben der üblichen
Dezimaldarstellung auch kleinere Einheiten in Gebrauch:
Eine Bogenminute (10 ) ist der 60-te Teil eines Grads.
Eine Bogensekunde (100 ) ist der 60-te Teil einer Bogenminute bzw.
der 3600-te Teil eines Grades.
Angaben mit Grad, Bogenminuten und Bogensekunden verwendet man
vor allem in der Geographie und in der Astronomie.
In Google Earth kann man für den Hörsaal WIN 1005 die geografischen
Koordinaten 50◦ 550 3000 N und 13◦ 200 0100 O ablesen. Wie lauten die
Angaben in Grad mit den gewohnten Nachkommastellen?
Vorkurs
TU Bergakademie Freiberg
5
Geographische Längen und Breiten
Positionen auf der Erdoberfläche lassen sich immer mittels zweier
Winkel (geogr. Länge (links) und Breite (rechts)) angeben:
Welchem Weg entspricht 1◦ (10 , 100 ) Breite auf der Erdoberfläche, wenn
man sich entlang eines Meridians bewegt? Gehen Sie von einer
kugelförmigen Erde mit 40000 km Umfang aus.
Vorkurs
TU Bergakademie Freiberg
6
Schätzen Sie Blickwinkel
In der Astronomie erfasst man Durchmesser und Abstände von Objekten
an der Himmelskugel ebenfalls über Winkelgrößen. Schätzen Sie:
den Winkel, den die gespreizte Hand (Ringfinger- bis
Daumenspitze); der Handrücken; der Zeigenfinger bei gestrecktem
Arm überdeckt,
die „Länge“ des Großen Wagens,
den Durchmesser der Sonne (des Mondes),
den Abstand Mizar-Alkor (mittlerer Deichsel(doppel)stern des
Großen Wagens),
die Auflösung des menschlichen Auges / die minimale Distanz
zweier getrennt sichtbarer Sterne,
den maximale Abstand des Gallileischen Jupitermondes Ganymed
zum Jupiter,
den Durchmesser des Jupiterscheibchens.
Vorkurs
TU Bergakademie Freiberg
7
Gon und Strich
Neben Grad und Radiant sind vereinzelt noch weitere Einheiten in
Gebrauch. Insbesondere wären zu nennen:
das Gon ist der 400-te Teil eines Vollkreises, ein rechter Winkel
entspricht also 100 gon.
Gebrauch vor allem im Vermessungs- und Markscheidewesen.
der nautische Strich ist der 32-te Teil eines Vollkreises.
Gebrauch vor allem in der Seefahrt zur Grobpeilung.
Kompassrose mit Strichteilung
Vorkurs
TU Bergakademie Freiberg
8
2 Winkelfunktionen und Trigonometrie
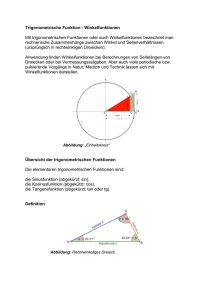
Unter dem Begriff Winkelfunktionen fasst man die Funktionen Sinus,
Kosinus, Tangens und Kotangens zusammen. Wir erinnern uns zunächst
an die Definition von Sinus und Kosinus am Einheitskreis.
1
sin ϕ
ϕ
ϕ
0
cos ϕ
1
Durch Skalieren der Skizze erhält man die klassischen
Winkelbeziehungen im rechtwinkligen Dreieck – doch dazu später.
Vorkurs
9
TU Bergakademie Freiberg
Betrachtet man Sinus und Kosinus in Abhängigkeit vom Winkel x,
entstehen zwei 2π-periodische Funktionen, deren Graphen lediglich um
π
2 gegeneinander verschoben sind:
Sinus
1
0
−1
−2π
−π
π
0
2π
Kosinus
1
0
−1
−2π
−π
π
0
Vorkurs
2π
TU Bergakademie Freiberg
10
Eigenschaften von Sinus und Kosinus
sin(x + 2π) = sin(x), cos(x + 2π) = cos(x),
d. h. Sinus und Kosinus sind 2π-periodisch,
sin(−x) = − sin(x), cos(−x) = cos(x),
d. h. der Sinus ist ungerade, der Kosinus gerade,
sin(x) = cos(x − π/2) und cos(x) = sin(x + π/2),
d. h. die Graphen sind um π/2 gegeneinander verschoben,
sin2 (x) + cos2 (x) = 1 (Satz des Pythagoras),
sin(x) = 0 ⇔ x = kπ mit k ∈ Z und
cos(x) = 0 ⇔ x = (k + 0.5)π mit k ∈ Z,
sin(x) ist auf [−π/2, π/2] streng monoton wachsend und
cos(x) ist auf [0, π] streng monoton fallend.
Vorkurs
TU Bergakademie Freiberg
11
Markante Funktionswerte
Es ist empfehlenswert, sich wenigstens einige Funktionswerte für Sinus
und Kosinus einzuprägen:
0/0◦
sin x
cos x
0
1
π
◦
6 /30
1
√2
3
2
π
◦
4 /45
√
2
√2
2
2
π
◦
3 /60
√
3
2
1
2
π
◦
2 /90
1
0
Aufgrund von Periodizität, Symmetrien usw. kann man daraus auf eine
Reihe weiterer Werte schließen. Zum Beispiel ist
√
3
sin 120◦ = sin 60◦ =
.
2
Vorkurs
TU Bergakademie Freiberg
12
Bestimmen Sie sämtliche Lösungen der Gleichungen
√
π
3
sin(2x + 1) = 0
und
cos( − 3x) =
.
2
2
Nutzen Sie die die Eigenschaften von Seite 11 wie auch die
Funktionswerttabelle auf Seite 12.
Zeichnen Sie die Graphen der Funktionen
f (x) = sin(2x + 1) = 0
und
g(x) = cos(
π
− 3x).
2
Interpretieren Sie Ihre Ergebnisse aus dem vorigen Beipiel graphisch.
Was ändert sich am Graphen einer Funktion y = f (x), wenn man x
durch kx (k > 0), −x bzw. x − c ersetzt? Was ändert sich wenn man
y = kf (x) (k > 0) statt y = f (x) betrachtet?
Vorkurs
TU Bergakademie Freiberg
13
Tangens und Kotangens
Der Tangens von x ist definiert durch
f : R \ k + 12 π : k ∈ Z → R,
x 7→ tan(x) :=
sin(x)
.
cos(x)
Der Kotangens von x ist definiert durch
f : R \ {kπ : k ∈ Z} → R,
x 7→ cot(x) :=
cos(x)
.
sin(x)
Im Gebrauch ist vor allem der Tangens.
Wichtige Eigenschaften:
tan und cot sind π-periodische Funktionen,
tan(−x) = − tan(x) und cot(−x) = − cot(x), d. h. beide
Funktionen sind ungerade,
tan ist auf (−π/2, π/2) streng monoton wachsend und
cot ist auf (0, π) streng monoton fallend.
Vorkurs
TU Bergakademie Freiberg
14
Graphische Darstellung
Tangens
Kotangens
4
cot(x)
1
2
x
tan(x)
0
sin(x)
0
−2
cos(x)
−4
−2π
−π
−1
2π
π
0
−1
0
1
Dargestellt sind die Graphen von Tangens und Kotangens sowie die
graphische Interpretation am Einheitskreis.
Vorkurs
TU Bergakademie Freiberg
15
Seiten-Winkel-Beziehungen im rechtwinkligen Dreieck
Im rechtwinkligen Dreieck sollten Sie zumindest folgende Beziehungen
(auswendig!) kennen:
Satz des Pythagoras: a2 + b2 = c2 .
Winkelbeziehungen:
sin β =
Flächeninhalt:
A=
b
c
1
2 ab
cos β = ac ,
tan β =
b
a
α
c
b
β
a
Machen Sie sich klar, dass die Winkelbeziehungen unmittelbar aus der
Definition von Sinus und Kosinus am Einheitskreis folgen.
Vorkurs
TU Bergakademie Freiberg
16
Seiten-Winkel-Beziehungen im allgemeinen Dreieck
Allgemein gelten in Dreiecken die folgenden Beziehungen:
Kosinussatz:
c2 = a2 + b2 − 2ab cos γ
Sinussatz:
a
sin α
Flächeninhalt:
A = 12 chc = 21 ab sin γ
=
b
sin β
=
c
sin γ
γ
b
a
hc
α
β
c
Man leite Sinus- und Kosinussatz unter Rückführung auf die
Beziehungen in rechtwinkligen Dreiecken her.
Vorkurs
TU Bergakademie Freiberg
17
Arkusfunktionen
Die Umkehrfunktionen der trigonometrischen Funktionen nennt man
Arkusfunktionen.
Da die trigonometrischen Funktionen auf R nicht eineindeutig sind,
muss man Einschränkungen auf bestimmte Intervalle vornehmen.
Man schränkt Kosinus
und Kotangens auf [0, π] sowie Sinus und
Tangens auf − π2 , π2 ein, und erhält die Umkehrfunktionen
arcsin : [−1, 1] → − π2 , π2 ,
y = arcsin(x) :⇔ x = sin y, y ∈ [− π2 , π2 ],
arccos : [−1, 1] → [0, π] , y = arccos(x) :⇔ x = cos y, y ∈ [0, π],
arctan : R → − π2 , π2 , y = arctan(x) :⇔ x = tan y, y ∈ [− π2 , π2 ],
arccot : R → [0, π] ,
y = arccot(x) :⇔ x = cot y, y ∈ [0, π].
mit Namen Arkussinus, Arkuscosinus, Arkustangens und
Arkuskotangens.
Vorkurs
18
TU Bergakademie Freiberg
Graphische Darstellung
π
π
arccot
arccos
π/2
π/2
0
0
arcsin
−π/2
−1
0
arctan
1
−π/2
−4
−2
0
2
4
Graphen sämtlicher Arkusfunktionen.
Vorkurs
TU Bergakademie Freiberg
19
Vielen Dank für Ihre Aufmerksamkeit
und einen guten Start ins Studium
an der TU Bergakademie Freiberg!
Originalfoto: Regi51
Vorkurs
TU Bergakademie Freiberg
20