Arcustangens, Arcussinus, Arcuscosinus – Übungsblatt

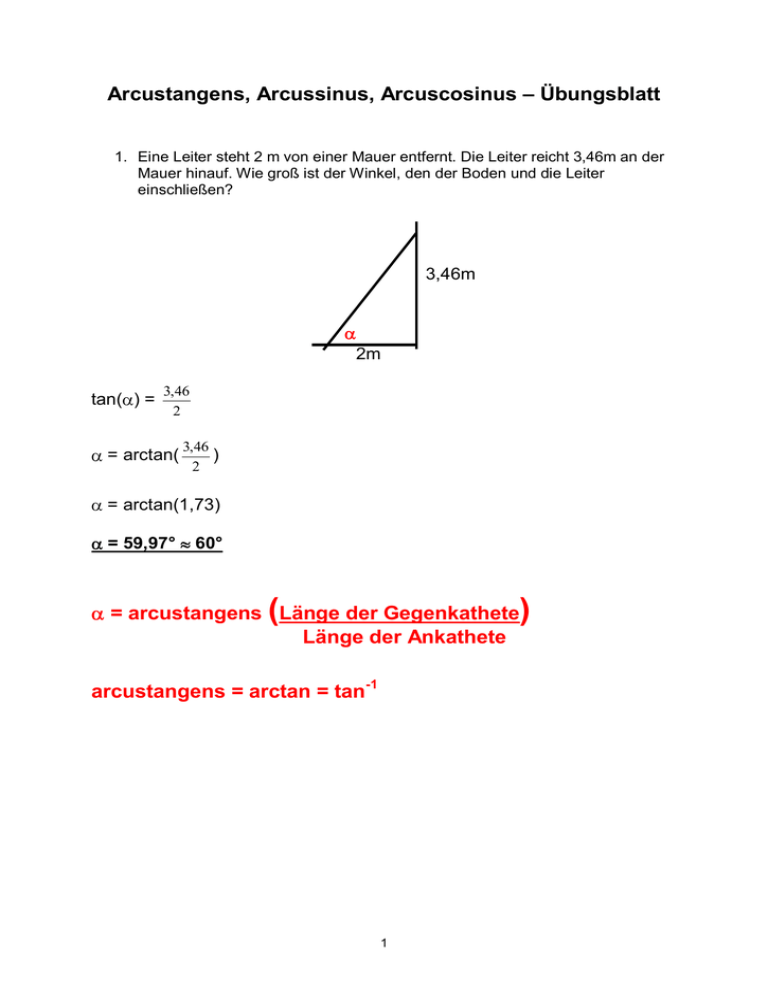
Arcustangens, Arcussinus, Arcuscosinus – Übungsblatt
1. Eine Leiter steht 2 m von einer Mauer entfernt. Die Leiter reicht 3,46m an der
Mauer hinauf. Wie groß ist der Winkel, den der Boden und die Leiter
einschließen?
3,46m
2m
tan( ) =
3,46
2
= arctan(
3,46
)
2
= arctan(1,73)
= 59,97°
60°
(
= arcustangens Länge der Gegenkathete
Länge der Ankathete
arcustangens = arctan = tan-1
1
)
2. Barbara möchte wissen, unter welchem Höhenwinkel sie die Spitze eines
42,21 m hohen Kirchturms betrachten muss, wenn sie 65 m vom Kirchturm
entfernt steht.
42,21m
65m
tan( ) =
42,21
65
= arctan(
42,21
)
65
= arctan(0,6494)
= 32,99°
33°
2
3. Eine 4 m hohe Leiter ist an einer Mauer angelehnt. Sie steht am Boden 2 m
von der Mauer entfernt. Wie groß ist der Winkel zwischen Leiter und Mauer?
4m
b
2m
b² = 4² -2²
b = 3,46
tan ( ) = (
2
)
3,46
= arctan(
2
)
3,46
= arctan(0,58)
= 30,11°
30°
3
oder kürzer:
2
4
sin( ) = ( )
2
4
= arcsin( )
= arcsin(0,5)
= 30°
(
= arcussinus Länge der Gegenkathete
Länge der Hypotenuse
arcussinus = arcsin = sin-1
4
)
4. Eine 966,88 m lange Seilbahn überwindet eine Höhe von 714 m. Wie groß ist
ihr Neigungswinkel?
714m
sin( ) = (
966,88m
714
)
966,88
= arcsin(
714
)
966,88
= arcsin(0,738)
= 47,6°
5
5. Eine 3 m hohe Leiter ist an eine Mauer angelehnt. Sie steht am Boden 1,5 m
von der Mauer entfernt. Wie groß ist der Winkel zwischen Leiter und Boden?
3m
1,5m
b² = 3² - 1,5²
b = 2,59
sin( ) = (
2,59
)
3
= arcsin(
2,59
)
3
= arcsin(0,866)
= 60°
oder kürzer:
cos( )=(
1,5
)
3
= arccos(
1,5
)
3
= arccos(0,5)
= 60°
(
)
= arcuscosinus Länge der Ankathete
Länge der Hypotenuse
arcuscosinus = arccos = cos-1
6
6. Von einem rechtwinkeligen Dreieck sind die Hypotenuse c=49,4 cm und die
Ankathete a=30,6cm von gegeben. Berechne die Größe der Winkel.
30,6cm
49,4cm
cos( ) = (
30,6
)
49,4
= arccos(
30,6
)
49,4
= arccos(0,6194)
= 51,73°
sin( ) = (
30,6
)
49,4
= arcsin(
30,6
)
49,4
= arcsin(0,6194)
= 38,27°
oder:
180°= 90° + 51,73° +
= 180° - 90° - 51,73°
= 38,27°
7
7. Eure Klasse geht ins Einkaufszentrum. Dort gibt es eine Rollband das 3,8 m
lang ist und eine Höhe von 2,9 m überwindet. Berechne den Winkel zwischen
Boden und Rollband. Berechne den Winkel zwischen Mauer und Rollband.
3,8m
2,9m
cos( ) = (
2,9
)
3,8
= arccos(
2,9
)
3,8
= arccos(0,763)
= 40,26°
sin( ) = (
2,9
)
3,8
= arcsin(
2,9
)
3,8
= arcsin(0,763)
= 49,73°
oder:
180°= 90° + 40,26° +
= 180° - 90° - 40,26°
= 49,74°
8