5. Dynamik: Kräfte, Newtonsche Gesetze

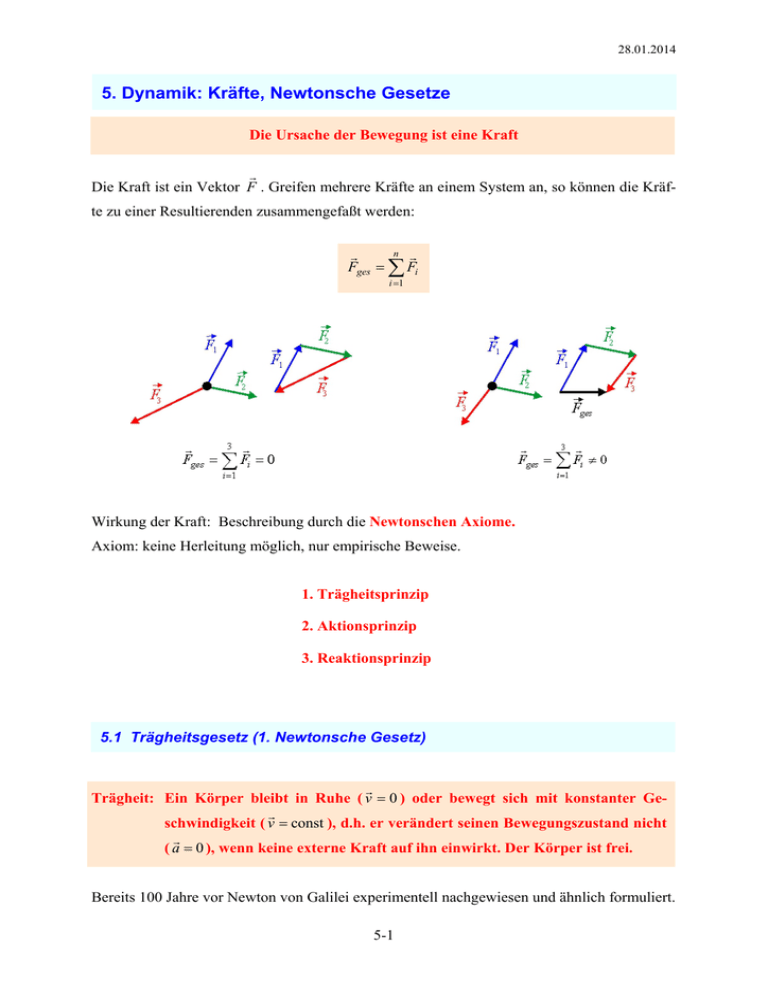
28.01.2014
5. Dynamik: Kräfte, Newtonsche Gesetze
Die Ursache der Bewegung ist eine Kraft

Die Kraft ist ein Vektor F . Greifen mehrere Kräfte an einem System an, so können die Kräfte zu einer Resultierenden zusammengefaßt werden:
n 

Fges   Fi
i 1
Wirkung der Kraft: Beschreibung durch die Newtonschen Axiome.
Axiom: keine Herleitung möglich, nur empirische Beweise.
1. Trägheitsprinzip
2. Aktionsprinzip
3. Reaktionsprinzip
5.1 Trägheitsgesetz (1. Newtonsche Gesetz)

Trägheit: Ein Körper bleibt in Ruhe ( v  0 ) oder bewegt sich mit konstanter Ge
schwindigkeit ( v  const ), d.h. er verändert seinen Bewegungszustand nicht

( a  0 ), wenn keine externe Kraft auf ihn einwirkt. Der Körper ist frei.
Bereits 100 Jahre vor Newton von Galilei experimentell nachgewiesen und ähnlich formuliert.
5-1
28.01.2014
Widerspricht etwas der alltäglichen Erfahrung: Bewegtes Auto stoppt nach Abschalten des
Motors (Kraft). Aristoteles: v = 0, wenn keine Kraft einwirkt = bevorzugter Ruhezustand =
Erde. Unterschied zu Newton: auch v = const. wenn keine Kraft einwirkt.
mit Motor:

Gegenkräfte FBrems : Gegenwind, Rollwiderstand


F
Motorkraft = Widerstandskräfte
 i  0  v  const.
ohne Motor:
F
Warum:

i

 0  a Brems
Beispiele:
Welcher Faden reißt? 3 Fälle sind möglich:
keiner: F zu klein, d.h. dünneren Faden nehmen
langsame Steigerung der Kraft:
oben:
FO  m  g  F
ruckartig. Trägheit der Masse:
unten:
FO  m  g < FU  F  m  a
Tablecloth.mpg
FU  F
tpaper.mpg
5.2 Aktionsprinzip: Kraft und Masse (2. Newtonsche Gesetz)
Kraft ist die Größe, die einen Körper dazu veranlaßt, seine Geschwindigkeit zu ändern.
Änderung der Geschwindigkeit = Beschleunigung:
Resultierende Kraft = Richtung der Beschleunigung


Fges  m  a
 kgm 
F  2   F N  = 1 Newton
 s 
gilt nur für m = const. ! (siehe Kap. 7.1 allgem. Def.)
5-2
28.01.2014
Die Masse widersetzt sich der Beschleunigung: „träge Masse“. Je größer m umso kleiner ist
die resultierende Beschleunigung a.
unabhängig von der Art der Kraft:
Elektron:
elektrisches Feld
Erde:
Gravitation
Beispiel:
1. ohne Bewegung (starrer Körper):  statisches Gleichgewicht

v 0 

F  0



v  0 FMauer  FZug  0


FMauer   FZug
actio = reactio
gleich groß aber entgegengesetzt

Die Kraft FMauer muß vorhanden sein für v  0
2. mit Bewegung:
Frage: Wie groß ist die Beschleunigung a des Autos ?


 F  FZ  0
FZ bewirkt eine Beschleunigung a:
5.3


FZ  m  a
Actio = Reactio (3. Newtonsche Gesetz)
Actio = Reactio
Die auf einen Körper einwirkende Kraft kann nicht aus diesem selbst stammen. Es muß
mindestens noch ein zweiter Körper vorhanden sein, von dem diese Kraftwirkung ausgeht. Kraft und Gegenkraft müssen auf zwei verschiedene Körper wirken.
5-3
28.01.2014
Baron Münchhausen sah das etwas anders:
Versuch: Federwaage (Video#5)
Frage: Wie weit wird die Feder im rechten Fall ausgelenkt ?
Die Auslenkung der Testfedern ist gleich groß! Gleichgültig wer die Reaktion erzeugt. Die
Kräfte erscheinen paarweise
Woher kommt m · g ?
Mond
F  0
Kreisbahn
Gezeiten
5-4
 v System  0
28.01.2014
Die Erde wird auch in Richtung Mond bewegt. Bewegung um den gemeinsamen Schwerpunkt. Meist vernachlässigbar, da Masse der Erde sehr groß im Vergleich zum Mond.
heben sich nicht auf, da Angriff auf unterschiedliche Körper 
G greift an Körper an
G‘ greift an Erde an
Körper fällt
Der Massenschwerpunkt bewegt sich aber nicht  vSystem = 0 da F1 = - F2
5.4 Fundamentale Kräfte
Kein direkter Kontakt zwischen den Körpern. Trotzdem besteht eine wechselseitige Wir-
kung = Wechselwirkung (WW). Schwer vorstellbar.
4 Grundlegende Arten:
Art der WW
Ursprung
Stärke
Reichweite
Gravitation
Masse
10-38
lang (r-2)
Elektromagnetische
WW
elektrische Ladungen
10-2
lang (r-2)
Schwache WW
Elementarteilchen
10-13
kurz (10-15 m)
Starke WW
Kernteilchen
1
kurz (10-15 m)
Gravitation:
Bestimmt u.a. Lauf der Planeten
Elektromagnetische: Elektrische u. magnetische Kräfte. Wesentlich stärker als Gravitation.
Beide haben eine große Reichweite.
Schwache WW:
Zwischen Elementarteilchen wie Elektronen, Protonen, Neutronen.
Starke WW:
Zwischen bestimmten Elementarteilchen (Neutronen, Protonen)
Reichweite nur auf atomarer Ebene.
Nichtsichtbare Kräfte. Ursache ? Wie wirken sie? Auch im Vakuum, ohne Kontakt.
Versuch der Physiker: Vereinheitlichung aller WW zu einer Kraft.
5-5
28.01.2014
5.4.1 Newtonsche Gravitationsgesetz
Annahme: 2 Massepunkte

F12 Kraft von m1 auf m2
m1 Ursache
m2 Wirkung auf


F12  F21 actio = reactio

 
r12  r2  r1


m m
r
F12    1 2 2  12
r12
r12

r12

r12,0  
r12
  6,67  10 11
Nm 2
kg 2
Gravitationskonstante
entgegengesetzt zu r12
Einheitsvektor von m1 nach m2
empirisches Gesetz: Bestimmung von  aus Experimenten. Naturkonstante oder „Mogelgröße“ zur Anpassung der Beobachtung an die Theorie. Warum genau diese Zahl ?



F ist ein Kraftfeld (Vektorfeld) da F  f ( r ) vom Ort abhängig ist.
Zentralkraft:
Kugel- oder radialsymmetrische Kraft, ausgehend vom Zentrum (Kugelmittelpunkt). Im Abstand r vom Mittelpunkt ist die Kraft const.
Beispiele:
Schwerefeld der Erde, Kraftfeld einer elektrischen Ladung
r 2 -Abhängigkeit (siehe auch Coulombsches Gesetz): im 3-dimensionalen Raum nimmt die
Wirkung einer Zentralkraft quadratisch ab. Verteilung der Wirkung auf einer Kugeloberfläche
O  r2  .
Für hypothetischen 2-dimensionalen Raum: Verteilung auf einen Kreisumfang U  r   also
r 1 -Abhängigkeit, für 4-dimensionalen Raum r 3 - Abhängigkeit.
5-6
28.01.2014
Beispiel: 2 Massen mit je 1 kg und 10 cm Abstand
F
6,67  10 11  1 1 Nm 2  kg  kg

 6,67 10  9 N
2
2
2
kg  m
(0,1)
für 2 Personen a 70 kg: F  6,67  10 9  4900  32,6  10-6 N
vgl. Anziehung Erde auf 1 kg: F  1  9,81  9,81 N (siehe 5.4.2)
d.h. meist venachlässigbar. Nicht bei sehr großen Massen (Kosmologie), oder im atomaren Abstand (AFM)!
5.4.2 Erdbeschleunigung g, Gewichtskraft G
Annahme: (Beweis Kap. 10.7 Tipler)

Ausgedehnte Kugelmasse:
Masse vereint im Kugelmittelpunkt:
homogene Massenverteilung
F  
Massepunkt
m E  m2
 m2  g ( r )
r2
g Erdbeschleunigung
g (r)   
Erdoberfläche:
mit
g (h)   
r  rE  h
m E  5,98  10 24 kg
r  rE ( rde )  6370 km ;
g ( h  0)   
allgemein:
mE
r2
mE
m
 9,81 2
2
rE
s
mE
rE  h  2
h Höhe über der Erdoberfläche
5-7
28.01.2014
Beispiel:
a) Für welche Höhe ist g = 0?
b) Für welche Höhe h ist g ( h ) 

1
g ( h  0)
2
h = 0: Erdoberfläche
mE
1 m
  2E
2
2 rE
( rE  h )
2rE2  rE2  2rE  h  h 2
 h  2640 km
in 350 km Höhe (ISS): g 350  0,9  g 0
Gewichtskraft G oder Erdanziehung


G  mg
mit
g  9,81
m
s2
g ist für alle Körper auf der Erde gleich, unabhängig von der Masse, d.h. unterschiedlich
schwere Massen (Feder, Eisenkugel) fallen gleich schnell bei Vernachlässigung des Luftwiderstandes): Fallzeit:
t
2h
(siehe Kap. 4.2.3)
g
siehe auch Versuch von Aristoteles (Vogelfeder im Vergleich mit Eisenkugel)
Versuch: Vakuumrohr Vergleich Feder - Eisenplatte (Video #7)
Kraft G hängt von der Masse des Körpers ab, nicht aber die Beschleunigung
g (r)   
mE
. Damit gilt: v  g  t
r2
und y  0,5  g  t 2 , d.h. die Fallgeschwindigkeit und
–zeit sind unabhängig von der Masse des Körpers. Widerspricht der täglichen „Erfahrung“.
5-8
28.01.2014
Versuch: Bestimmung von g (Video #6)
Messen der Fallzeit der Eisenkugel mit 3 Zählern
s
1
g  t2
2
g
2s
t2
(siehe 4.1.3 für a = const.) 
s [m]
t [s]
g [m s-2]
0,1
0,14
10,2
0,4
0,28
10,2
0,9
0,42
10,2
g ist örtlich nicht konstant: (meist vernachlässigbar)
1.
g hängt ab vom Ort:
Erde nicht exakt rund und inhomogene Dichteverteilung
Für sehr große m z. B. Meer meßbar: Südl. Indien entspricht
ca. 110m tiefe „Delle“, bei Neu-Guinea 80m hoher „Berg“
 
 g ( r ) Gravitationsfeld = Vektorfeld
5-9
28.01.2014
Gewichtskraft G ist damit vom Ort abhängig. Die Masse m dagegen ist unabhängig vom
Ort = charakteristische Größe eines Körpers.
Wie sie zustande kommt ist noch unbekannt: Gibt es eine unteilbare „Elementarmasse“
Beispiel: Waagrechter Wurf auf dem Mond.
Erde
Mond
1 kg
Masse
m
1 kg
„schwere Masse“
mg
1 kg  9,81
„träge Masse"

Horizontaler Stoß a

1 kg  a
m
s2
~ 1 kg 

9,81 m
6 s2

1 kg  a
d.h. Gewichtheben ist leichter auf dem Mond, Billardspielen ist identisch.
„schwere Masse“ und „träge Masse“ sind nicht mehr verwendete Bezeichnungen, da die Massen gleich sind. Besser:
“Schwere“ und „Trägheit“ sind Eigenschaften der Masse
Einsteinsche Äquivalenzprinzip: Gleichheit der Gravitations- und Trägheitskraft.
Ausgangspunkt der allgemeinen Relativitätstheorie (siehe Kap. 13.5).
Umgangssprache:
Ich wiege 90 kg ist falsch!
Richtig:
Meine Masse beträgt 90 kg
Mein Gewicht = Gewichtskraft G  m  g  90 N
2. g nimmt ab mit der Höhe ( Abstand 2). Raumschiff auf einer Kreisbahn um die Erde in
großer Höhe. Heißt Schwerelosigkeit: g  0 ?
Nein: Zentripetalkraft wird benötigt sonst keine Kreisbahn (Raumschiff hat kein Seitenruder,
also woher kommt die Kreisbahn ?)
Zentripetalbeschleunigung

v2
aR 
r
wird benötigt für Kreisbahn (Kap. 4.3.4)
Zentripetalkraft

v2
FR  m
r
zur Erde hin gerichtet
gegeben ist die Erdbeschleunigung g = f(r):
Wenn für gegebene r, g:
g  a R : freier Fall
g  a R : Schwerelosigkeit
g  a R : Flucht (kein Kreis)
5-10
28.01.2014
z.B.: Flugzeug in 10 km Höhe mit
Zentripetalbeschleunigung:
v  1000 km/h v 
106 m
m
 278
3600 s
s

v2
m
2782
m2
aR 

 0,012 2  g (h  10 km)
2
r (6400  10)  1000 s m
s
Erdradius (km)
in der Regel vernachlässigbar gegen 9,81 m s-2
9,799 m s-2
das Flugzeug stürzt ab ohne zusätzliche Kraft = Auftriebskraft durch Flügel
Offene Fragen nach Newton:
1. Wie schnell ändert sich die Kraftwirkung, wenn eine Masse sich entfernt oder ihre Masse
ändert? Unendlich schnell ? Lösung durch Einsteinsche Relativitätstheorie. Maximal mit c.
2. Wieso kollabiert ein statisches Universum nicht auf Grund der Gravitation? Daß es expan-
diert, entdeckte Hubble erst 1929. Selbst Einstein glaubte noch an das statische.
5.5 Bezugssysteme und Scheinkräfte
5.5.1 Inertialsysteme
Inertialsysteme sind unbeschleunigt
Inertia = Trägheit
Gedankenexperiment: Unbeschleunigtes System v = const. (ohne Reibung)
In beiden Systemen keine Kraft nach 1. Newtons Axiom (v = 0 oder v = const.)
Wagen:
vWagen  0 = const.
vWagen = 0
1. Wahl des Bezugsystems (entspricht Videokamera):
2. S’:
S:
vBuch  0
vBuch  0
relativ zum Wagen
relativ zur Erde
vBuch  0
vBuch  vWagen
5-11
relativ zum Wagen
relativ zur Erde
28.01.2014
3. Ergebnis:
a) Es gilt das 1. Newtonsche Gesetz (Trägheitsgesetz). Daher der Name Inertialsystem.
b) Die Geschwindigkeit ist abhängig vom Bezugssystem: v Buch 
x x2  x1

t
t
Die Ortsdifferenz erfordert einen Bezugspunkt.
Auch das Auge erkennt Geschwindigkeiten nur relativ zur Umgebung.
c) Es gibt keine Möglichkeit zu entscheiden, wer sich bewegt: Erde oder Wagen, d.h. es
gibt keinen ausgezeichneten Ruhepunkt. Beide haben daher das Recht sich als ruhend
zu betrachten und es gelten in beiden Systemen die Newtonschen Gesetze.
d) Es gibt keine absolute Position oder Raum: Newtonsche Relativität
e) Es gibt keine Möglichkeit zu entscheiden, ob 2 aufeinander folgende Ereignisse am
gleichen Ort stattfinden. z.B. Ball springt im Wagen auf und ab.
e) Newton: die Zeit ist absolut, d.h. unabhängig von der Geschwindigkeit.
Erweiterung durch Einsteinsche allgemeine Relativitätstheorie (siehe Kap. 13)
5.5.2 Beschleunigtes System
System 2 (S): Erde: in Ruhe
Buch bleibt in Ruhe vBuch = 0
(Inertialsystem), da keine Kraft auf das
Buch wirkt (reibungsfrei)
System 1 (S’): Wagen: beschleunigt
Buch wird nach hinten beschleunigt, obwohl keine Kraft auf das Buch wirkt.
Widerspruch zum 1. Newtonschen Axiom
5-12
28.01.2014
Auflösung: Einführung einer Scheinkraft ma’ = - ma da System 1 kein Inertialsystem
ist. Ein Beobachter auf der Erde sieht das Buch in Ruhe. Eine Kamera im Zug (kein Inertialsystem) sieht das Buch nach hinten fliegen ohne Grund.
Scheinkraft: Es gibt keinen Körper, der diese Kraft erzeugt. Die Wirkung aber ist real.
Entsteht nur in beschleunigten Bezugssystemen, deshalb auch Trägheitskraft genannt.
Für Kreisbewegungen gilt: Beschleunigtes System
5.5.3 Zentrifugalkraft
Beispiel: rotierende Scheibe
Inertialsystem
beschleunigtes System (Kreisbewegung)
im System a (Inertialsystem): Beobachter extern (od. Kamera über dem Tisch fest auf
dem Boden montiert:
Drehbewegung der Masse m:  Zentripetalkraft FR  m   2  r
wird benötigt um das Teil
auf der Kreisbahn zu halten; wird von Seil erledigt. Trennen des Seil: Masse fliegt weg.
System b (kein Inertialsystem): Beobachter auf der rotierenden Scheibe (od. Kamera
auf dem Tisch fest montiert). Rotation heißt beschleunigte Bewegung:
Beobachtung: Scheibe rotiert nicht und wenn Seil getrennt wird fliegt Masse nach außen:
m liegt in Ruhe auf der Scheibe: v = 0. Beim Trennen des Seils fliegt sie weg, d.h. wird beschleunigt ohne sichtbare Kraft  Widerspruch zum 1. Newtonsche Axiom!
5-13
28.01.2014
Einführen einer Scheinkraft:



FZ  m  aZ   FR
Zentrifugalbeschleunigung:
 


aZ    v    a R
Zentrifugalkraft
keine echte physikalische Kraft. Wenn es eine echte physikalische Kraft wäre, müsste die
Masse nach dem Durchtrennen des Seils auch mit einer radialen Komponente wegfliegen.
Fliegt aber rein tangential!
Beispiele: Diskuswerfer, Schleifscheibe und Funken
nur tangentiale Bewegung
Aufgabe: Berechnen Sie die Zentrifugalbeschleunigung der Erdrotation
in München ( = 48° Breite). Radius der Erde: RE = 6,38·106 m
aZ 

FZ
  2  r   2  RE cos 
m
d v 2 r
2
1
 

 7,27  10 5
dt r r  T 24  3600
s
aZ  0,0225
m
s2
Senkrechter Anteil aS: Wirkung auf g:
aS  aZ  cos   0,0151
aS
 0,154%
g
Tangentiale Anteil at: Zusätzlich eine geringfügige Ablenkung  g’
r
 
s 
m
v 
s
m
aZ  2 
s 
Erdrotation Äquator
6,38·106 m
7,27  10 5
464
0,0337
Sonnenumlauf
1,5·1011 m
1,99 107
3·105
0,00594
2,5·1020 m  25000 Lj
0,8 1015
2·105
1,6·10-10
Rotation Galaxie
1 
5-14
28.01.2014
5.5.4 Corioliskraft
bewegte Masse im rotierenden System (kein Inertialsystem)
System a:
System b
Beobachter außen:
Beobachter auf drehender Scheibe:
Inertialsystem
kein Inertialsystem
gerader Flug: keine Kraft
Kurvenflug: Ablenkung durch eine zusätzliche Scheinkraft: Corioliskraft
für v = const: Wurfgeschwindigkeit nicht Rotationsgeschw.
Ball erreicht nach t  r / v den Rand
In dieser Zeit hat sich der Rand um
s  r    r    t  v    t 2 unter dem Ball weiter bewegt.
mit r  v  t
Beobachter auf Scheibe sieht die Ablenkung der Kugel nach
hinten und schließt auf eine Beschleunigung s  t 2
vgl. konstante Beschleunigung: s 
s
1
aC  t 2  v    t 2
2
FC  2  m  v  
vektoriell:
gilt auch für v  const.
5-15
1 2
at
2
(siehe 4.1.3)
aC  2  v  

 
FC  2  m  v   
tangential
28.01.2014
Aufgabe:
Sie lassen am Äquator in einem Zug, der sich mit mit vZ = 100 km/h nach Osten bewegt einen
Ball nach unten fallen (Fallhöhe h = 1m). Wo kommt der Ball im Zug an: Vor, hinter oder
genau senkrecht unter dem Startpunkt?
a) In einem Inertialsystem (Zug) besteht nach Newton kein Unterschied ob vZ = 0 od. vZ =
const. Der Zug wird daher im folgenden als ruhend betrachtet: vZ = 0
b) Steht der ruhende Zug in einem Inertialsystem? Nein, er bewegt sich mit der rotierenden
Erde.
Erdansicht von oben auf den Nordpol
Rotiationsgeschwindigkeit der Erde:
va  ra  
vb  rb    va
Abwurfgeschw. va in 1 m Höhe ist größer
als die Geschwindigkeit vb am Boden.
Vergleichbar einem Wagen mit linearer Bewegung, der während des Fluges des Balls
nach unten auf vb abgebremst wird. Der Ball
landet in Erddrehrichtung vor dem Startpunkt.



Coriolisbeschleunigung: aC  2  vF   
Wie groß ist die Verschiebung?
c) Fallhöhe h 
1 2
gt F
2
 Fallzeit
2h
g
tF 
und Fallgeschwindigkeit: vF  g  t
keine Vektoren, da am Äquator vF  
aC  2vF    2 g    t
tF
 vC   aC  dt  g    t 2  vC 0 mit vC 0  0 ;   7,27  10 5
 2h 
1
1
s   g    t dt  g    t F3  g     
3
3
 g 
0
2
3
2
1
s
1
8h 3
 
 22 μm meist vernachläßigbar
3
g
Für h = 100 m: s = 22 mm
Weitere Anwendung: Hoch- und Tiefdruckgebiete, Foucaultsches Pendel
5-16
28.01.2014
5.6 Kontaktkräfte (Feder, Reibung)
5.6.1 Federkraft FR
im statischen Gleichgewicht: v = 0
 
F  FR  0


 

FR   F   K ( x  x0 )   K  x
K
Federkonstante
Hooke´sche Gesetz
N
 m 
x0 meist = 0 Ruhelage (freie Wahl der Koordinaten)
Ziehen:
x  0
neg. Kraft = Rückstellkraft (FR entgegen x)
Hooke´sche Gesetzt gilt nur im elastischen Bereich, kleine Auslenkung, keine
plastischen Verformungen.
Beispiel:
masselose Feder


Im statischen Gleichgewicht: keine Bewegung v  0  Fges  0
 


G  FR  0 ;
mg  K  x  0
x in g Richtung
m
K  x
g
Federwaage, Messen von x
5-17
28.01.2014
5.6.2 Reibung
Beobachtung: Schieben einer Kiste: Zuerst großer Widerstand bis Kiste in Bewegung 
Haftreibung. Dann etwas kleinerer Widerstand  Gleitreibung
Versuch: Förderband: Übergang von Haft- auf Gleitreibung (Video #8)
Haftreibung: Gedankenexperiment: von was hängt die Reibung ab?
FN = Normalkraft  zur reibenden Fläche
doppelte Masse  doppelte Reibungskraft
Größere Fläche = größere Reibung
aber kleinerer Auflagedruck

 FReibung  f (m  g )
 FReibung  f ( A)
Haftreibung (keine Bewegung): für v = 0:


FH   H  FN
F ≤ FH


FH  FN
Näherung !
Betrag wg. unterschiedlichen Richtungen von FH und FN
µH Haftreibungszahl
H = f (Oberflächenbeschaffenheit, Material)
für F > FH  Bewegung  Gleitreibung


FG  G  FN
G   H
Näherung !
Betrag wg. unterschiedlichen Richtungen von FG und FN
µG Gleitreibungszahl
G = f (Geschwindigkeit) für große v
5-18
28.01.2014
Ursache der Reibung:
- mikroskopische Rauhigkeit
- Wechselwirkung der Moleküle
- noch nicht vollständig verstanden (Tribologie)
Tabelle 5.1: Näherungswerte einiger Reibungszahlen
Materialien
H
G
Stahl auf Stahl
0,7
0,6
Blech auf Stahl
0,5
0,4
Kupfer auf Gußeisen
1,1
0,3
Glas auf Glas
0,9
0,4
Teflon auf Teflon
0,04
0,04
Teflon auf Stahl
0,04
0,04
Gummi auf Beton (trocken)
1,0
0,8
Gummi auf Beton (naß)
0,3
0,25
Gewachster Ski auf Schnee (0°C)
0,1
0,05
Gummi auf Asphalt
0,8.....1,1
0,7....0,9
Eis-Eis (0°C)
0,05.....0,19
0,02
Beispiel: Schiefe Ebene
Frage: max. Steigungswinkel kurz vor dem Gleiten
Kräfte am Körper:
in y-Richtung:
 Fy  FN  FGy  0
wg. ay = 0
FGy  m  g  cos 
FN  m  g  cos 
5-19
28.01.2014
 Fx   FGx  FR  0
in x-Richtung:
gerade noch keine Bewegung: ax = 0
FGx  m  g  sin 
FR  FN   H
Mit
Haftreibung
FGx  FR
mg  sin    H m g  cos 
Ergebnis:
 H  tg
für größere Winkel: Gleiten d.h. a x  0
 Fx   FGx  FR  m  a x
ax entgegen x-Richtung
 m g  sin   G m  g  cos   m  a x
Ergebnis: a x  g (sin    G  cos  )
Antrieb
Bremsen
Sonderfall: ax = 0 für G 
Beispiel Reifen:
beschleunigtes Gleiten
sin 
 tg  vx = const (Gleiten mit konstanter Geschw.)
cos 
Rollen ̂ Haftreibung. Durchdrehen oder Blockieren ̂ Gleitreibung
 ABS-System.
Breitreifen: Einfluß der Fläche über Verformung (nicht bei steifen Reifen). Mehr Kleben als
Reibung.
5-20