Grundwissen 6-1

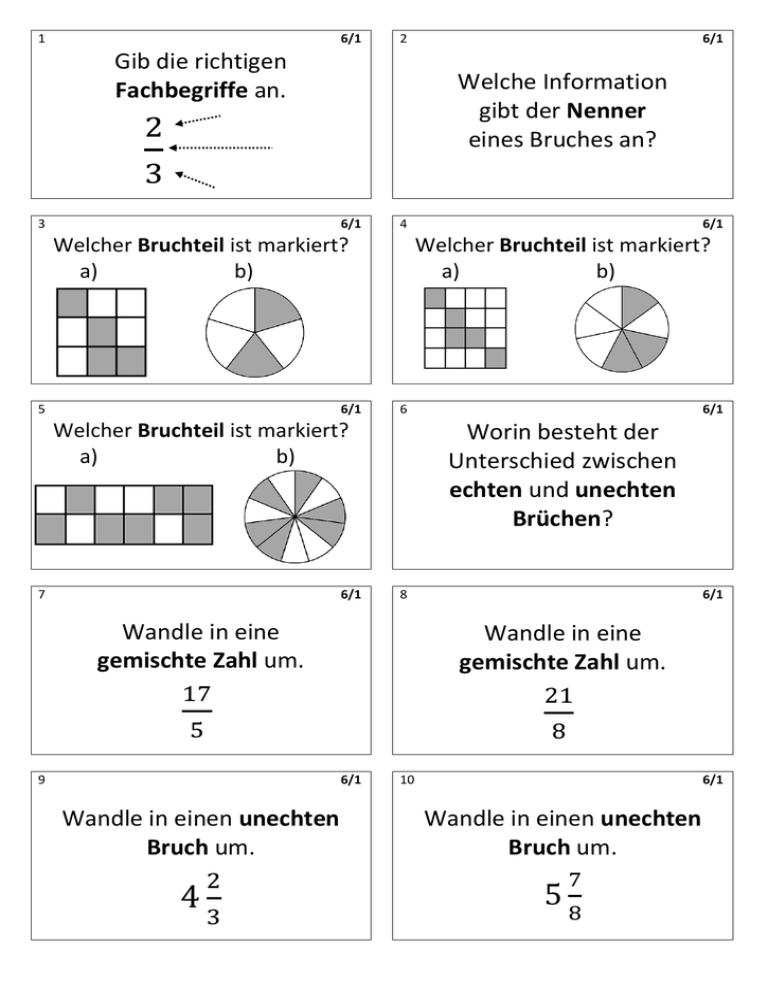
1
6/1
2
Gib die richtigen
Fachbegriffe an.
3
Welche Information
gibt der Nenner
eines Bruches an?
6/1
4
Welcher Bruchteil ist markiert?
a)
b)
5
6/1
6/1
6
8
6/1
Wandle in eine
gemischte Zahl um.
6/1
Wandle in einen unechten
Bruch um.
6/1
Worin besteht der
Unterschied zwischen
echten und unechten
Brüchen?
Wandle in eine
gemischte Zahl um.
9
6/1
Welcher Bruchteil ist markiert?
a)
b)
Welcher Bruchteil ist markiert?
a)
b)
7
6/1
10
6/1
Wandle in einen unechten
Bruch um.
2-L
6/1
1-L
Er gibt an, in wie viele
gleich große Teile
ein Ganzes zerlegt wurde.
6/1
Zähler
Bruchstrich
Nenner
4-L
6/1
3-L
6/1
6-L
6/1
5-L
6/1
Bei einem echten Bruch ist der
Zähler immer kleiner als der Nenner,
bei einem unechten Bruch ist der
Zähler immer größer als der Nenner.
8-L
6/1
7-L
6/1
10-L
6/1
9-L
6/1
11
6/1
12
Was bedeutet
„einen Bruch erweitern“?
13
Was bedeutet
„einen Bruch kürzen“?
6/1
14
6/1
6/1
Kürze soweit wie möglich.
a)
Gibt es eine Zahl, mit der
man einen Bruch nicht
erweitern oder kürzen darf?
15
6/1
b)
16
Kürze soweit wie möglich.
a)
6/1
Kürze soweit wie möglich.
b)
17
6/1
Erweitere auf den Nenner 20.
a)
19
b)
18
6/1
Erweitere auf den Nenner 54.
c)
a)
6/1
Wie addiert bzw. subtrahiert
man zwei gemeine Brüche?
b)
c)
20
6/1
Berechne.
Gib das Ergebnis als vollständig
gekürzte gemischte Zahl an.
12-L
6/1
Zähler und Nenner eines Bruches
werden durch dieselbe Zahl dividiert.
Der Wert des Bruches ändert sich
dabei nicht!
14-L
6/1
11-L
6/1
Zähler und Nenner eines
Bruches werden mit derselben Zahl
multipliziert. Der Wert des Bruches
ändert sich dabei nicht!
13-L
6/1
a)
Ja, die 0.
b)
16-L
6/1
15-L
6/1
a)
b)
(Für die Zwischenschritte gibt
es mehrere Möglichkeiten.)
18-L
a)
20-L
6/1
b)
c)
17-L
a)
6/1
6/1
b)
c)
19-L
1. Schritt: Man bestimmt den
Hauptnenner und macht die
Brüche gleichnamig.
2. Schritt: Man addiert bzw.
subtrahiert die Zähler, aber behält
den gemeinsamen Nenner bei.
6/1
21
6/1
22
Berechne.
Gib das Ergebnis als vollständig
gekürzten Bruch an.
23
Berechne.
Gib das Ergebnis als vollständig
gekürzte gemischte Zahl an.
6/1
24
Berechne im Kopf.
Gib das Ergebnis als vollständig
gekürzten Bruch an.
25
26
Berechne.
Gib das Ergebnis als vollständig
gekürzten Bruch an.
28
Wie multipliziert man zwei
gemischte Zahlen?
6/1
Berechne.
Gib das Ergebnis als vollständig
gekürzte gemischte Zahl an.
6/1
Berechne.
Gib das Ergebnis als vollständig
gekürzten Bruch an.
6/1
29
6/1
Wie lautet die
Regel zum Multiplizieren
zweier gemeiner Brüche?
6/1
27
6/1
6/1
Wie multipliziert man
einen gemeinen Bruch
mit einer ganzen Zahl?
30
6/1
Berechne.
Gib das Ergebnis als vollständig
gekürzten Bruch an.
22-L
6/1
21-L
6/1
24-L
6/1
23-L
6/1
oder
26-L
6/1
25-L
oder besser
28-L
oder besser
6/1
Verwandle die ganze Zahl
in einen Bruch mit dem
Nenner 1.
Rechne danach normal mit der Regel
27-L
6/1
Man muss die gemischten Zahlen
zuerst in unechte Brüche
umwandeln, danach rechnet man
normal mit der Regel
weiter.
30-L
6/1
weiter.
6/1
29-L
6/1
31
6/1
32
Berechne.
Gib das Ergebnis als vollständig
gekürzten Bruch an.
33
Wie dividiert man
zwei gemeine Brüche?
6/1
34
Berechne.
Gib das Ergebnis als vollständig
gekürzten Bruch an.
35
6/1
6/1
Berechne.
Gib das Ergebnis als vollständig
gekürzten Bruch an.
6/1
36
6/1
Wie dividiert man
einen gemeinen Bruch
durch eine ganze Zahl?
Wie dividiert man zwei
gemischte Zahlen?
[Bzw. wie dividiert man eine ganze
Zahl durch einen Bruch?]
37
6/1
38
Berechne.
Gib das Ergebnis als vollständig
gekürzten Bruch an.
39
Berechne.
Gib das Ergebnis als vollständig
gekürzten Bruch an.
6/1
Berechne.
Gib das Ergebnis als vollständig
gekürzten Bruch an.
6/1
40
6/1
Was bedeutet
das Symbol
?
32-L
6/1
31-L
6/1
34-L
6/1
33-L
6/1
36-L
6/1
35-L
6/1
Man bildet den Kehrwert des
zweiten Bruchs und multipliziert
anschließend die beiden Brüche.

Verwandle die ganze Zahl
in einen Bruch mit dem
Nenner 1.
Rechne danach normal mit der Regel
Man muss die gemischten Zahlen
zuerst in unechte Brüche
umwandeln, danach rechnet man
normal mit der Regel
weiter.
weiter.
38-L
6/1
37-L
6/1
40-L
6/1
39-L
6/1
steht für die Menge aller
positiven rationalen Zahlen
mit der Zahl 0
(das sind alle natürlichen Zahlen, alle
positiven Brüche und die Zahl 0).
41
6/1
42
Welches Rechenzeichen kann
man statt eines Bruchstrichs
schreiben?
43
6/1
6/1
Wie wandelt man einen
gemeinen Bruch in einen
Dezimalbruch um?
44
6/1
Erweitere auf eine Zehnerpotzenz
im Nenner und wandle in einen
Dezimalbruch um.
Erweitere auf eine Zehnerpotzenz
im Nenner und wandle in einen
Dezimalbruch um.
45
46
6/1
Wandle in einen
Dezimalbruch um.
47
Wandle in einen
Dezimalbruch um.
6/1
48
Wandle in einen
Dezimalbruch um.
49
6/1
Wandle in einen
Dezimalbruch um.
6/1
Wandle in einen
Dezimalbruch um.
6/1
50
6/1
Wandle in einen
Dezimalbruch um.
42-L
6/1
41-L
- Zähler durch Nenner
dividieren ODER
- auf Nenner 10; 100; 1000…
erweitern und umwandeln
6/1
:
(Die 2. Methode ist nicht immer möglich.)
44-L
6/1
43-L
6/1
46-L
6/1
45-L
6/1
ODER
48-L
6/1
47-L
6/1
ODER
50-L
6/1
ODER
49-L
6/1
ODER
51
6/1
52
Wandle in einen
Dezimalbruch um.
53
Wandle in einen
Dezimalbruch um.
6/1
54
Wie wandelt man einen
endlichen Dezimalbruch in
einen gemeinen Bruch um?
55
6/1
6/1
6/1
Wandle in einen
gemeinen Bruch um.
0,16
56
6/1
Wandle in einen
gemeinen Bruch um.
Wandle in einen
gemeinen Bruch um.
3,41
0,25
57
6/1
58
6/1
Wandle in einen
gemeinen Bruch um.
Wandle in einen
gemeinen Bruch um.
0,125
0,0325
59
6/1
60
6/1
Wandle in einen
gemeinen Bruch um.
Wandle in einen
gemeinen Bruch um.
3,58
4,2
52-L
6/1
51-L
6/1
54-L
6/1
53-L
6/1
- Zähler: Schreibe die Zahl aus allen
Dezimalen in den Zähler.
- Nenner: Notiere hier die
entsprechende Stufenzahl
(10; 100; 1000; …).
- Ganze: Schreibe die Ganzen davor.
56-L
6/1
55-L
6/1
58-L
6/1
57-L
6/1
60-L
6/1
59-L
6/1
61
6/1
10,35
6/1
64
Wandle in einen
gemeinen Bruch um.
65
66
Wandle in einen
gemeinen Bruch um.
68
Wandle in einen
gemeinen Bruch um.
6/1
Wandle in einen
gemeinen Bruch um.
6/1
Wandle in einen
gemeinen Bruch um.
6/1
Wandle in einen
gemeinen Bruch um.
6/1
69
6/1
Wandle in einen
gemeinen Bruch um.
6/1
67
6/1
Wie wandelt man einen unendlich
periodischen Dezimalbruch, bei
dem die Periode gleich nach dem
Komma beginnt, in einen
gemeinen Bruch um?
Wandle in einen
gemeinen Bruch um.
63
62
70
6/1
Wandle in einen
gemeinen Bruch um.
62-L
6/1
61-L
6/1
- Zähler: Schreibe die Periode in den
Zähler.
- Nenner: Notiere im Nenner die Zahl,
die aus so vielen Ziffern 9 besteht, wie
die Länge der Periode vorgibt.
- Ganze: Schreibe die Ganzen davor.
64-L
6/1
63-L
6/1
66-L
6/1
65-L
6/1
68-L
6/1
67-L
6/1
70-L
6/1
69-L
6/1
71
6/1
72
Erkläre das Abrunden von
ganzen Zahlen oder
Dezimalbrüchen.
73
6/1
Erkläre das Aufrunden von
ganzen Zahlen oder
Dezimalbrüchen.
6/1
74
6/1
Runde wie angegeben.
Runde wie angegeben.
(G = Ganze)
(h = Hundertstel)
123,8 (G)
6,983 (h)
75
6/1
76
6/1
Runde wie angegeben.
Runde wie angegeben.
(z = Zehntel)
a) 67,2345 (h)
12,057 (z)
b) 7,987 (z)
77
6/1
Runde wie angegeben.
78
6/1
Wie addiert bzw. subtrahiert
man zwei Dezimalbrüche?
a) 123,354 (h)
b) 2,009 (z)
79
6/1
Berechne im Kopf.
a) 23,4 + 5,38 =
b) 70,357 – 4,12 =
80
6/1
Berechne.
24,812 + 300,4 + 18,5673 =
72-L
6/1
71-L
Die zu rundende Ziffer
wird um 1 erhöht,
wenn eine der Ziffern
5; 6; 7; 8; 9 folgt.
74-L
Die zu rundende Ziffer
bleibt unverändert,
wenn eine der Ziffern
0; 1; 2; 3; 4 folgt.
6/1
73-L
6,983  6,98
76-L
6/1
75-L
6/1
12,057  12,1
b) 7,987  8,0
6/1
77-L
1. Schritt: Man bringt die Dezimalbrüche durch
Anhängen von Endnullen auf
gleich viele Dezimalstellen.
2. Schritt: Man addiert bzw. subtrahiert
Ziffern mit gleichem Stellenwert.
6/1
6/1
a) 123,354  123,35
b) 2,009  2,0
WICHTIG: Achte beim schriftlichen Addieren und
Subtrahieren darauf, dass die Kommas der
Dezimalbrüche genau untereinander stehen!
80-L
6/1
123,8  124
a) 67,2345  67,23
78-L
6/1
79-L
a)
b)
6/1
81
6/1
82
6/1
Berechne.
Berechne.
12,98 – 4,0082 + 3,2 – 0,056 =
(45,32 + 4,907) – (34,564 – 6,02) =
83
6/1
84
Berechne im Kopf.
Wie multipliziert man
zwei Dezimalbrüche?
85
6/1
6/1
a)
2,5 0,3 =
b)
0,02 0,03 =
c)
1,2 0,5 =
86
6/1
Berechne.
Wie dividiert man
einen Dezimalbruch durch
eine natürliche Zahl?
a) 32 0,024 =
b) 8,61 6,02 =
c) 1,5 1000 =
87
6/1
88
Berechne.
Berechne.
79,482 : 6 =
89
6/1
625,48 : 4 =
6/1
Wie dividiert man
einen Dezimalbruch
durch einen Dezimalbruch?
90
6/1
Berechne.
4,97 : 3,5 =
82-L
6/1
=
(45,320 + 4,907) – (34,564 – 6,020) =
50,227
–
28,544
=
21,688
(45,32 + 4,907)
– (34,564 – 6,02)
84-L
6/1
6/1
12,98 – 4,0082 + 3,2 – 0,056 =
12,98 + 3,2 – 4,0082 – 0,056 =
16,18 –
4,0642 =
12,1158
83-L
6/1
1. Schritt: Man multipliziert die beiden
Dezimalbrüche zunächst
ohne Komma.
2. Schritt: Man setzt das Komma so, dass
das Ergebnis so viele
Dezimalstellen besitzt, wie die
beiden Faktoren zusammen.
a) 0,75
b) 0,0006
c) 0,06
86-L
81-L
6/1
85-L
Man dividiert zunächst nach dem
bekannten schriftlichen Verfahren
(wie bei zwei natürlichen Zahlen).
6/1
a) 0,768
b) 51,8322
Überschreitet man jedoch beim
Herunterholen der Stellen im Dividenden
das Komma, so muss man auch im Ergebnis
das Komma an dieser Stelle setzen.
c) 1500,0 = 1500
88-L
6/1
87-L
90-L
6/1
89-L
6/1
1. Schritt: Man verschiebt das Komma bei Dividend
UND Divisor um so viele Stellen nach
rechts, bis der Divisor eine natürliche Zahl
ist, also kein Komma mehr besitzt.
2. Schritt: Man dividiert wie in .
Dabei muss man aber beachten:
Man setzt im Ergebnis ein Komma, wenn
man im Dividenden das Komma
überschreitet.
= 49,7 : 35
= 1,42
6/1
91
6/1
92
6/1
Berechne.
Berechne.
15,606 : 3,06 =
624 : 0,06 =
93
6/1
Gib für die beiden gemeinen
Brüche die entsprechenden
Dezimalbrüche an.
a)
a)
6/1
Gib für die beiden gemeinen
Brüche die entsprechenden
Dezimalbrüche an.
a)
Gib für die beiden gemeinen
Brüche die entsprechenden
Dezimalbrüche an.
a)
b)
6/1
Gib für die beiden gemeinen
Brüche die entsprechenden
Dezimalbrüche an.
b)
6/1
Gib für die beiden gemeinen
Brüche die entsprechenden
Dezimalbrüche an.
b)
98
b)
99
6/1
Gib für die beiden gemeinen
Brüche die entsprechenden
Dezimalbrüche an.
6/1
a)
b)
96
b)
97
6/1
Gib für die beiden gemeinen
Brüche die entsprechenden
Dezimalbrüche an.
b)
95
a)
94
b)
100
6/1
Gib für die beiden Dezimalbrüche
die entsprechenden gemeinen
Brüche an.
a) 0,5
b) 0,2
92-L
6/1
91-L
= 62400 : 6
=…
= 10 400
94-L
= 1560,6 : 306
=…
= 5,1
6/1
a) 0,25
a) 0,6
a)
b)
6/1
a) 0,4
6/1
b) 0,375
97-L
b) 0,8
100-L
6/1
a) 0,125
6/1
b) 0,2
95-L
b) 0,875
98-L
6/1
a) 0,5
6/1
a) 0,625
93-L
b) 0,75
96-L
6/1
b) 0,
99-L
6/1
a) 0,
b) 0,
101
6/1
Gib für die beiden Dezimalbrüche
die entsprechenden gemeinen
Brüche an.
a) 0,25
a) 0,125
6/1
Gib für die beiden Dezimalbrüche
die entsprechenden gemeinen
Brüche an.
Gib für die beiden Dezimalbrüche
die entsprechenden gemeinen
Brüche an.
a) 0,6
6/1
Gib für die beiden Dezimalbrüche
die entsprechenden gemeinen
Brüche an.
a) 0,4
6/1
b) 0,375
104
b) 0,875
105
6/1
Gib für die beiden Dezimalbrüche
die entsprechenden gemeinen
Brüche an.
b) 0,75
103
a) 0,625
102
b)
106
6/1
Gib für die beiden Dezimalbrüche
die entsprechenden gemeinen
Brüche an.
a) 0,
b) 0,8
b) 0,
107
6/1
108
6/1
109
6/1
110
6/1
102-L
6/1
a)
b)
104-L
a)
6/1
a)
6/1
b)
103-L
b)
106-L
6/1
a)
6/1
a)
101-L
b)
105-L
6/1
a)
b)
b)
108-L
6/1
97-L
6/1
110-L
6/1
109-L
6/1