Ferromagnetismus: Heisenberg-Modell
Werbung
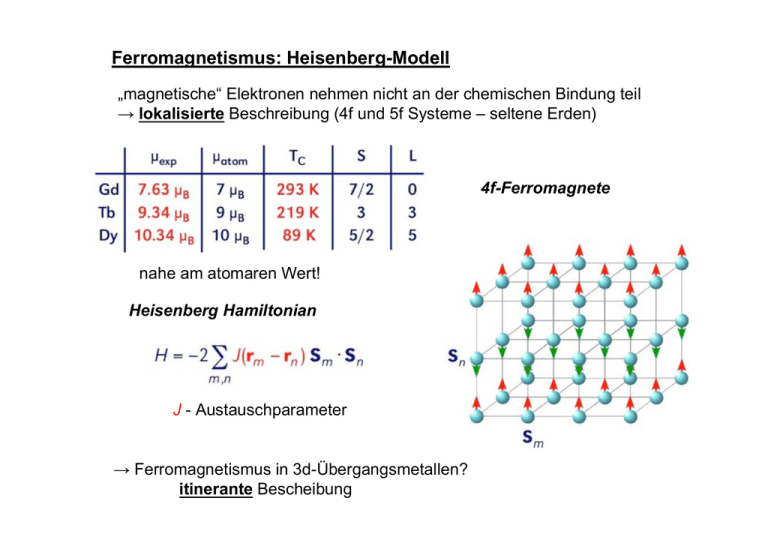
Ferromagnetismus: Heisenberg-Modell „magnetische“ Elektronen nehmen nicht an der chemischen Bindung teil → lokalisierte Beschreibung (4f und 5f Systeme – seltene Erden) 4f-Ferromagnete nahe am atomaren Wert! Heisenberg Hamiltonian J - Austauschparameter → Ferromagnetismus in 3d-Übergangsmetallen? itinerante Bescheibung Modellsystem: freies Elektronengas Eigenwertgleichung Energieeigenwerte E Zahl der Zustände N Zwei Spins (Pauli-Prinzip) mit ebenen Wellen: Besetzt bis k = kF (Fermi-Niveau) E ~ k2 Volumen des k-Raums Volumen jedes Zustands im k-Raum Abstand der Punkte 2π / L Erhöhung der Zustandsdichte g(E) = Anzahl der Zustände im Energieintervall dE mit bzw. freies Elektronengas: Zustandsdichte aus Fermi Energie EF bei T = 0 K → Je größer die Ladungsträgerdichte N/V, desto höher liegt EF aus und Zustandsdichte bei EF : Oft: Renormierung der e--Masse m→ m* (fast) freies Elektronengas im periodischen Gitter E ~ k2 Endliche Temperaturen: Fermi-Verteilung f(E,T) chemisches Potential μ Definiert durch f(E,T) = 0.5 für T=0 T≠0 Maxwell-Boltzmann-Verteilung und μ = EF Für Metalle unterhalb des Schmelzpunkts kT << EF Fermifläche ist definiert als die Punkte im k-Raum, deren Energie gleich dem chemischen Potential μ ist Wenn die Fermifläche in einer Bandlücke liegt → Halbleiter / Isolator Hamiltonoperator für das freie Elektronengas im Magnetfeld siehe WMI Skript bereits erwähnt, jetzt nochmal Überraschenderweise gilt: genauer oder Anmerkung: Langevin Diamagnetismus und Paramagnetismus haben den identischen Hamilton, dieser wird aber für das Elektron im Wasserstoffpotential betrachtet „Zeeman“ Effekt des freien Elektronengases: Pauli Paramagnetismus Vernachlässigung des Bahndrehimpulses (freie e- !) modifizierte Energie-Impulsbeziehung Daraus folgt die Pauli-Suszeptibilität : Integrand durch EF ersetzen sehr kleiner Effekt !! Bandferromagnetismus (itinerant) „magnetische“ Elektronen nehmen an der chemischen Bindung teil → itinerante („bandartige“) Beschreibung (3d Übergangsmetalle) 3d-Ferromagnete Werte weit weg vom atomaren magnetischen Momenten mit oder ohne Bahnmoment → woher kommen die starken Abweichungen der experimentell bestimmten magnetischen Momente? starre Verschiebung der Bänder mit Spin up oder down gegeneinander („rigid band behavior“) Bandferromagnetismus – Stoner Kriterium Energiebilanz der magnetische Ordnung: (Energieschuld) Energiegewinn durch Magnetisierung M 1 μB pro e- λ - Molekularfeld Energiegewinn (= Ferromagnetismus) für ΔEtot < 0 Stoner Kriterium – Stoner Verstärkung U – Maß für die Stärke des Molekularfelds Oft wird auch I (Austauschintegal) verwendet: → hohe Zustandsdichte an der Fermikante favorisiert FM Verstärkung: „fast“ ferromagnetisches Metall (z.B. Pt, Pd) Energieänderung im Feld Energieänderung minimieren → Modifikation der Pauli-Suszeptibilität um „Reale“ Bandstruktur von Fe, Co, Ni Molekularfeld – Austauschwechselwirkung Molekularfeld der „Stäke“ λ Anschaulich: Magnetisierung eines einzelnen (freien) Elektrons im Feld der anderen (magnetisierten) Elektronen (↔ Pauli-Suszeptibilität) → „Henne – Ei Problem“ Erster Versuch: Dipol-Dipol Wechselwirkung Zwei magnetische Dipole μ1 und μ2 im Abstand r Abschätzung für Parallelstellung, Moment ~ μB, Abstand ~ Angstrom Das entspricht ca. 1.2 K → nur bei sehr tiefen Temperaturen relevant → Molekularfeld muß andere Ursachen haben Molekularfeld – Austauschwechselwirkung Zweiter Versuch: Heisenbergmodell Austauschintegral J = Überlapp der Wellenfkt. Häufige Näherungen: nur nächste-Nachbar-Wechselwirkung; Jij = J = const. Betrachte nun die mittlere WW eines Spins j mit dem restlichen Ensemble <S> „mean field“ Näherung <S> wirkt auf einen Spin wie ein effektives Magnetfeld Oder ersetze B durch Weißsches Molekularfeld ~ 103 T Molekularfeld (Korrelationen werden vernachlässigt)











