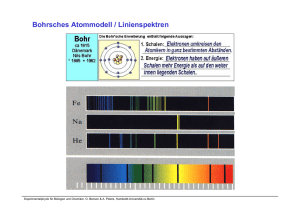
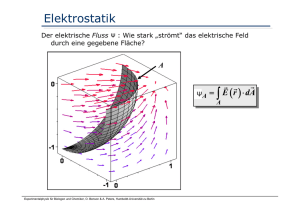
Maxwellsche Gleichungen

Maxwellsche Gleichungen
James Clerk
Maxwell
(1831-1879)
bisherige Grundgleichungen ...
Ladungen erzeugen elektrische Felder:
r
ρ
div E =
ε0
Es gibt keine Ladungen, die magnetische Felder erzeugen:
r
div B = 0
Ströme erzeugen magnetische (Wirbel-)Felder:
r
r
r
∂E
rot B = μ 0 j + μ 0ε 0
∂t
Zusätzlicher Term mit enormen
Konsequenzen:
Maxwellscher Verschiebungsstrom
Das statische E-feld wirbelfrei, aber zeitabhängige B-Felder erzeugen ein
elektrisches Wirbelfeld:
r
r
∂B
rot E = −
∂t
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Maxwellsche Gleichungen (1873)
Verknüpfung von
elektrischen Feldern und Ladungsverteilung (1)
Das elektrische Feld hat die Ladungsdichte als Quelle
magnetischen Feldern und Strömen (4)
Quelle der zeitlichen Änderung des elektrischen
Feldes und der Wirbelstärke des magnetischen Feldes
ist die Stromdichte j.
elektrischen und magnetischen Feldern (3)
Quelle der zeitlichen Änderung des Magnetfeldes ist
die“Wirbelstärke“ des elektrischen Feldes
Quellfreiheit von magnetischen Feldern (2)
Das Magnetfeld hat keine Quellen
r r ρ
(1) ∇ ⋅ E =
ε0
r r
(2) ∇ ⋅ B = 0
r
r r
∂B
(3) ∇ × E = −
∂t
r
r
r r
∂E
(4) ∇ × B = μ 0 j + ε 0 ⋅ μ 0 ⋅
∂t
⎛ ∂ ⎞
⎜ ∂x ⎟
⎜ ⎟
r ⎜ ∂ ⎟
∇=
= Nabla − Operator
⎜ ∂y ⎟
⎜ ⎟
⎜⎜ ∂ ⎟⎟
⎝ ∂z ⎠
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
James Clerk
Maxwell
(1831-1879)
Einordnung der Maxwelltheorie
Ziel moderner Physik: Vereinigung der verschiedenen Theorien
Magnetismus
Elektrostatik
Elektromagnetismus
(Maxwelltheorie)
Gravitations WW
(Einstein-Theorie)
schwache WW
(Fermitheorie)
elektroschwache WW
(Glashow-Salam-Weinberg)
starke WW
(Quanten-Chromo-Dynamik)
Große Vereinigung
Supergravitation
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Elektromagnetische Wellen
Maxwellsche Gleichungen
• Annahme:
es gibt keine (freien) Ströme und keine (freien) Ladungen
(betrachte z.B. Vakuum)
• Frage: können dann trotzdem E- und B-Felder existieren?
Maxwellgleichungen:
( A)
(C )
r r
∇⋅E = 0
r r
r&
∇ × E = −B
( B)
( D)
r r
∇⋅B = 0
1 r r r&
∇× B = E
μ0 ⋅ ε 0
• Antwort: ja, wenn sie erst einmal existieren, können sie sich gegenseitig
„am Leben erhalten“.
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Wellengleichung/Quellen des EM Feldes
Schritt 1
sich änderndes E-Feld
erzeugt B-Feld
Schritt 2
Schritt 3
sich änderndes B-Feld
erzeugt E-Feld
sich änderndes B-Feld
erzeugt sich
änderndes E-Feld, das
wiederum sich
änderndes B-Feld
erzeugt,...
ABER: irgendwann irgendwo müssen zeitlich
variierende Ladungen oder Ströme E- und B-Feld
erzeugt haben
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Hertzscher Dipol [1]
r
E
• Aufklappen eines
r
B
Schwingkreises bestehend
aus Kondensator und
Leiterschleife (Spule)
• beim Schwingkreis ist E-Feld auf Raum zwischen Kondensatorplatten,
B-Feld auf Innenraum der Spule beschränkt
• beim linearen Oszillator (d) erstrecken sich E- und B-Feld
über den gesamten Raum und sind „untrennbar verbunden“, daher :
elektromagnetisches Feld
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Hertzscher Dipol [2]
• Hertzscher Oszillator stellt ein
schwingungsfähiges System für E- und BFelder dar.
• E- und B-Felder können zu Stehwellen angeregt werden. Randbedingung
I = 0 an den Enden legt die Form der möglichen Stehwellen fest
• Stehwellen für I wie bei Stab mit fest eingespannten Enden
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Hertzscher Dipol [3]
3
1
r
E
+
–
+
–
4
2
+
–
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
–
+
Hertzscher Dipol [4]
E
B
λ
„Fernfeld“
„Nahfeld“ bis r ≈λ
• im Fernfeld lösen sich E- und B-Felder vom Dipol
• lokal ist das Feld eben, E und B stehen senkrecht
aufeinander und senkrecht zur Ausbreitungsrichtung
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Hertzscher Dipol [5]
• Abstrahlungscharakteristik
(lokale) Energiestromdichte eines EM-Feldes wird beschrieben durch
Poyntingvektor:
Richtung
und Betrag
r
von S im Fernfeld
I
r r r
1 r r
S = E×H =
E×B
μ0
Poyntingvektor
- maximal in Ebene, die
Dipol teilt und senkrecht
zum Strom I steht
- verschwindet entlang der
Achse des Dipols
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Elektromagnetisches Spektrum
Licht
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Lichtspektrum
Energie [eV]:
Frequenz [Hz]:
Wellenlänge [nm]:
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Elektromagnetische Wellengleichung
Wie erhält man im freien Raum (i.e., keine Ströme oder Ladungen) aus den
Maxwellgleichungen eine Wellengleichung ?
r
r
∂B
rot E = −
∂t
r
r
⎛ ∂B ⎞
rot (rot ( E )) = − rot ⎜⎜ ⎟⎟
⎝ ∂t ⎠
r
r
∂E
rot B = μ 0ε 0
∂t
r
r
2
⎛ ∂B ⎞
∂ E
rot ⎜⎜ ⎟⎟ = μ 0ε 0 2
∂t
⎝ ∂t ⎠
r
r
∂ E
rot (rot ( E )) = − μ 0ε 0 2
∂t
2
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Elektromagnetische Wellengleichung
Kombinierte Gleichungen von vorhin
Aus der Mathematik
r
2
r
∂ E
rot (rot ( E )) = − μ 0ε 0 2
∂t
r
r
r
rot (rot ( E )) = − div (grad ( E )) + grad (div ( E ))
r
⎛ ∂2
∂2 ⎞ r
∂2
= ⎜⎜ 2 + 2 + 2 ⎟⎟ E = Δ E
∂z ⎠
∂y
⎝ ∂x
=0
Damit folgt die elektromagnetische Wellengleichung
⎛ ∂2
∂2
∂2 ⎞ r r
∂2 r r
− ⎜⎜ 2 + 2 + 2 ⎟⎟ E (r , t ) = − μ 0ε 0 2 E (r , t )
∂y
∂z ⎠
∂t
⎝ ∂x
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Erinnerung: Wellengl. d. Mechanik
Harmonische Wellen in 3D sind Lösungen der Wellengleichung
2
2
2
⎞ r
⎛
∂2 r
∂
∂
∂
2
y (r , t ) − c ⎜⎜ 2 + 2 + 2 ⎟⎟ y (r , t ) = 0
2
∂z ⎠
∂t
∂y
⎝ ∂x
r
r = ( x, y , z )
Oder in Kurzschreibweise
r
r
∂2 r
2 2
y (r , t ) − c ∇ y (r , t ) = 0
2
∂t
r ⎛∂ ∂ ∂⎞
∇ = ⎜⎜ , , ⎟⎟
⎝ ∂x ∂y ∂z ⎠
Oder noch kürzer mit dem „Lapace-Operator“
r
∂2 r
2
y (r , t ) − c Δy (r , t ) = 0
2
∂t
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
⎛ ∂2
∂2
∂2 ⎞
Δ = ⎜⎜ 2 + 2 + 2 ⎟⎟
∂y
∂z ⎠
⎝ ∂x
Wellengleichungen im Vergleich
Wellengleichung der Mechanik („skalar“)
2
2
2
⎛
⎞ r
∂2 r
∂
∂
∂
2
y (r , t ) − c ⎜⎜ 2 + 2 + 2 ⎟⎟ y (r , t ) = 0
2
∂t
∂y
∂z ⎠
⎝ ∂x
Wellengleichung der Elektrodynamik
∂2 r r
∂2
∂2 ⎞ r r
1 ⎛ ∂2
⎜⎜ 2 + 2 + 2 ⎟⎟ E (r , t ) = 0
E (r , t ) −
2
∂t
μ 0ε 0 ⎝ ∂x ∂y ∂z ⎠
Vergleich zeigt für die Ausbreitungsgeschwindigkeit (i.e. die Lichtgeschwindigkeit):
c =
1
2
μ 0ε 0
c =
1
μ 0ε 0
Für jede Komponente Ex, Ey, Ez des elektrischen Vektorfeldes gilt eine eigene
Wellengleichung. Diese sind aber nicht völlig unab-hängig voneinander (wg. der beiden
anderen Maxwellgleichungen)!
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Lichtgeschwindigkeit
Seit 1983 ist c0
eine definierte
Größe …
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Wellengleichung
einfacher in 1D:
2 r
∂2 r
∂
2
E
x
t
−
c
E ( x, t ) = 0
(
,
)
2
2
∂t
∂z
und noch einfacher in 1D für nur eine E-Feld Komponente:
2
∂2
∂
2
E
(
x
,
t
)
−
c
E y ( x, t ) = 0
y
2
2
∂t
∂x
Vergleich mit Mechanik erlaubt sofort folgende Schlüsse über Eigenschaften EM-Wellen
1. jede Lösung der Wellengleichung lässt sich durch
Überlagerung von ebenen Wellen beschreiben
r r
r r
E = E0 ⋅ cos k ⋅ r − ω ⋅ t + ϕ
(
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
)
r r
r r
E = E0 ⋅ cos k ⋅ r − ω ⋅ t + ϕ
(
Wellengleichung
2. Phasengeschwindigkeit
(„Lichtgeschwindigkeit“)
c=
1
μ0 ⋅ ε 0
3. Wellenlänge (räumliche Periodizität):
r
λ = 2π k
4. Schwingungsdauer/Frequenz
T = 2π ω
(zeitliche Periodizität)
5. Wellenvektor/Wellenzahl
(Ausbreitungsrichtung)
6. EM-Wellen können
- interferieren
- gebeugt werden
- gebrochen werden
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
r
r
er = k k
k
)
Wellengleichung/Transversalwellen
aus Maxwellgleichungen:
E- und B-Feld stehen senkrecht zur
r
Ausbreitungsrichtung e r , sind also
k
Transversalwellen
-
E- und B-Feld stehen senkrecht zueinander
rr
ek
y
λ
B0z
z
E0y
-
-
x
und sind proportional zueinander:
r
rr r
B = c ⋅ ek × E
damit gibt es 2 orthogonale lineare Polarisationen, hier
r r
E ⊥ ey
und
r r
E ⊥ ex
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Wellengleichung/Energietransport
• EM-Wellen können (auch im Vakuum !) Energie transportieren.
• Dies wird beschrieben durch den Poyntingvektor, mathematische eine
„Energiestromdichte“, der die Intensität angibt:
Ebene Welle
(
)
r
r ⎛ r r 1⎞
r 2⎞ r
1 r r
2
⎛
S =
E × B = c ⋅ ε 0 ⋅ E × ⎜ ekr × E ⋅ ⎟ = ⎜ c ⋅ ε 0 ⋅ E ⎟ ekr
⎝
⎠
μ0
c⎠
⎝
(
)
• Die lokale „Energiedichte“ des EM Feldes wird konsistent damit beschrieben durch:
Ebene Welle
dW
dV
r 2 1 r 2⎞
r
1⎛
⎜⎜ ε 0 ⋅ E +
B ⎟⎟ = ε 0 ⋅ E
=
2⎝
μ0
⎠
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
2
Wellengleichung/Impulsübertragung
r
r r
S = (1 /μ 0 ) E ⋅ B
r
r r
S = (1 /μ 0 ) E × B
c
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Ebene Welle
Wellengleichung/Impulsübertragung
Crooke's Radiometer
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
Wellengleichung/Impulsübertragung
Nichols Radiometer
Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin