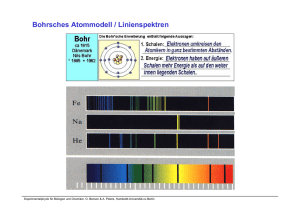
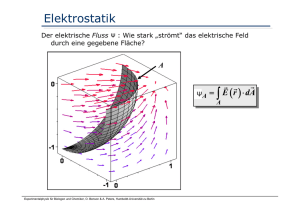
Der elektrische Strom - Humboldt
Werbung

Der elektrische Strom Bisher: Ruhende Ladungen Jetzt: Abweichungen vom elektrostatischen Gleichgewicht Elektrischer Strom Æ Transport von Ladungsträgern Damit Ladungen einen Strom bilden, müssen sie „frei“ sein. Materialen für welche dies möglich ist bezeichnet man als Leiter. Beispiele Vakuum: Elektronen in Elektronenröhre Gasen: Neonröhre Flüssigkeiten: Ionen in Autobatterie Festkörper: Leiter: Elektronen im Metall Halbleiter: Zahl der Elektronen stark von Temperatur abhängig Nichtleiter: (fast) keine freien Elektronen Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Der elektrische Strom / Definitionen Elektrische Stromstärke verschobene Ladung ΔQ I = = Δt Zeit Coulomb [I ] = = Ampere Sekunde Stromdichte r I Strom j = = A Fläche r r I = ∫ j ⋅ dA Stromrichtung Æ Bewegungsrichtung der positiven Ladungsträger (Also auch: Bewegung von Elektronen im Leiter entgegengesetzt zur Stromrichtung) Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Wirkungen des elektrischen Stroms Magnetische Wirkung Ein stromdurchflossener Leiter ist von einem Magnetfeld umgeben (Oerstedt 1820) Auf stromdurchflossene Leiter wirkt im Magnetfeld eine Kraft Also zusammen: Zwischen zwei oder mehr stromdurchflossenen Leitern wirken Kräfte R r dr r dA r r B Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Einschub: Strom als Basiseinheit Strom ist eine der 7 Basiseinheiten des SI-Systems d.h. sie muss definiert werden. (wie z.B. Meter, Kilogramm, und Sekunde) Eichung über die magnetische Wechselwirkung I1=I2=1A André-Marie Ampère (1775-1836) Die Stromstärke I hat den Wert 1 A, wenn zwei im Abstand d = 1 m angeordnete parallele, geradlinige und unendliche lange Leiter mit vernachlässigbaren Querschnitt von dem gleichen Strom I durchflossen werden und pro l = 1 m Leiterlänge eine Kraft F = 2 · 10-7 N aufeinander ausüben. Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin 1m Wirkungen des elektrischen Stroms Wärmewirkung In den meisten Leitern (Ausnahme: freie Teilchen im Vakuum) erzeugt ein Stromfluss Wärme d.h. es wird Energie umgewandelt ... Beispiele: Heizdraht, Glühlampe, ... Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Wirkungen des elektrischen Stroms Chemische Wirkung Anode Kathode + – I Elektrolyse Abscheidung von Substanzen Quantitative Ausmessung möglich Faraday 1833: Menge der Zersetzungsprodukte ist proportional zur durchgeleiteten Elektrizitätsmenge Die abgeschiedene/erzeugte Substanzmenge im mg/C nennt man das elektrochemische Äquivalent eines Stoffes Möglichkeit zu einer alternativen Definition elektrischer Einheiten! Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Elektrolyse Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Elektrolyse Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Das Ohmsche Gesetz Stromfluss bei Vorhandensein einer Potentialdifferenz (Spannung) Gesucht wird ein gesetzmäßiger Zusammenhang zwischen Strom und angelegter Spannung Beispiel: Entladung eines Plattenkondensators Kurzschluss mit Leiter Æ schnelle Entladung „Geschwindigkeit“ der Entladung ist proportional Stromstärke I Spannung Beobachtungen: I nimmt mit der Länge des Leiters ab I nimmt mit dem Querschnitt des Leiters zu I ist stoffspezifisch Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Das Ohmsche Gesetz Ursache des Elektrischer Strom bewegte Ladung q Leiter − + Anlegen einer Spannung bewirkt elektrisches Feld Coulombkraft beschleunigt Elektronen r E e v= ⋅E ⋅t me – U ⇒ Geschwindigkeit müsste ständig steigen Dies wird nicht beobachtet! Erinnerung: strömende Flüssigkeit: Strömungswiderstand, Reibungseffekte Im Metall: I=U/R v(t) vD Stöße der Elektronen mit Gitteratomen ⇒ Ausbilden einer konstanten Driftgeschwindigkeit vD ⇒ Konstanter Strom Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Steigung a=e·E·/me Zeit t Das Ohmsche Gesetz Beim Stromfluss durch einen Leiter sind Strom I und Spannung U proportional: U U R= I großer Widerstand kleiner Widerstand I R wird als Ohmscher Widerstand bezeichnet. Er ist bei konstanter Temperatur unabhängig von I Einheit [R ] = V = Ω = Ohm A Ohmsches Gesetzt gilt z.B. nicht für Glühbirnen, da Erwärmung bei hohem Strom Widerstand vergrößert. Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Georg Simon Ohm ( 1789-1854 ) Das Ohmsche Gesetz Ohmsches Gesetz gilt zum Beispiel auch für elektrische Leitung in elektrolytischen Flüssigkeiten Spannung zwischen Messköpfen des Spannungsmessers ist proportional zum Strom und zum Abstand zwischen den Messköpfen Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Spezifischer Widerstand Der elektrische Widerstand eines Leiters hängt vom atomaren Aufbau und von der Geometrie des Leiters ab. l l: Länge des Leiters R = ρ⋅ A: Querschnittsfläche A ρ:spezifischer elektrischer Widerstand (unabhängig von Geometrie) [ρ]=Ω·m σ=1/ρ: Leitfähigkeit [σ]=1/(Ω·m) Material Eisen Kupfer Platin Germanium Silizium dest. Wasser Glas Papier Porzellan Teflon Bernstein ρ [Ωm] 9.81·10-8 1.68·10-8 1.05·10-7 0.5 2·103 2.3·105 1013-1014 1015-1016 1010-1016 1·1017 >1017 Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Leiter: Widerstand steigt mit Temperatur Halbleiter: Widerstand sinkt mit Temperatur Isolatoren: indifferent Temperaturabhängigkeit von R Der elektrische Widerstand eines Leiters ändert sich im allgemeinen mit der Temperatur. Wie stark und mit welchem Vorzeichen ist Temperaturabhängig. Leiter 1. Klasse: Cu, Al, Fe Æ Widerstand steigt mit steigender Temperatur Æ „positive Temperature coefficient“, PTC Leiter 2. Klasse: C, Si, Halbleiter, elektrolytische Leiter Æ Widerstand fällt mit steigender Temperatur Æ „negative Temperature coefficient“, PTC Für den spezifischen Widerstand gilt dabei im Falle kleiner Temperaturänderung näherungsweise eine lineare Abhängigkeit: ρT = ρ 0 (1 + αT ) Mit dem „Temperaturkoeffizienten“ Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin ρT − ρ 0 α= Tρ T Leitfähigkeit Leitfähigkeit σ • Metalle: σ nimmt mit steigendem T ab, da Beweglichkeit der Ladungsträger abnimmt. (PTC-Widerstände, Positive Temperature Coefficient) • Halbleiter: σ nimmt mit steigendem T zu, da Ladungsträgerdichte zunimmt. Die Änderung der Beweglichkeit spielt keine Rolle (NTCWiderstände) Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Beispiele für Ladungstransport In einem Stromkreis fließt 1 A. Wie viele Elektronen bewegen sich in 1 s durch den Querschnitt eines Leiters? ΔQ N ⋅ e 1.6 ⋅ 10 −19 A / s 1 I= = =N⋅ = 1A ⇒ N = ≈ 6 ⋅ 1018 −19 Δt Δt 1s 1.6 ⋅ 10 Zusatzfrage: Wie schnell bewegen sich die Elektronen im Metall? Zunächst: Elektronendichte ? im Metall ca. 1 freies Elektron pro Atom nCu ≈ N Anzahl der Cu − Atome N N = = = A* ⋅ ρM Volumen V M / ρM M 6 ⋅ 1023 ⋅ mol ⋅ 8.9g = = 8.4 ⋅ 1022 cm −3 3 mol ⋅ 63.6g ⋅ cm ρM : Massendichte N A : Avogadrozahl M * : molare Masse ( Atomgewicht ) Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Beispiele für Ladungstransport Mit welcher mittleren Geschwindigkeit vD („Driftgeschwindigkeit“) bewegen sich die Elektronen falls ein Strom I=1A durch einen Leiter mit einem Querschnitt von 1mm2 fließt? Ladung Q durch Fläche A in Zeit Δt: Q= e·ne·dx·A = e·ne·vD· Δt·A vorher: ne ≈ 8·1022 cm-3 für Kupfer; bewegliche Ladungsdicht ρe= e·ne r v dx vD = Q I ⋅ Δt I = = e ⋅ ne ⋅ Δt ⋅ A e ⋅ ne ⋅ Δt ⋅ A e ⋅ ne ⋅ A C ⋅ 1000mm 3 1A s = = −19 −3 −19 22 2 1.6 ⋅ 10 C ⋅ 8 ⋅ 10 cm ⋅ 1mm 1.6 ⋅ 10 C ⋅ 8 ⋅ 1022 ⋅ 1mm 2 mm m ≈ 0.08 ≈ 0.3 s h 1 Weinbergschnecke: maximal 4 m/h Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin r A Einfacher Stromkreis Schaltbild für einfachen Stromkreis = verlustfrei Leiter (keine Potentialveränderung) Gleichspannungsquelle: zeitlich konstante Spannung Ideale Messgeräte für Strom bzw. Spannung: kein Einfluss auf Ströme und Spannungen im Stromkreis. Strom Leiter Gleichspannungsquelle + - U Spannung gleiches Potential Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin R Messgeräte Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Kirchhoff‘sche Regeln: Knotenregel Knotenregel: „Die vorzeichenrichtige Summe aller Ströme, die in einen Netzwerkknoten herein- oder herausfließen, ist immer 0A.” I1 I5 I4 ∑I = I 1 I2 Gustav Robert Kirchhoff (1824 –1887) + I2 + I3 + ... = 0 I3 Die Richtung der Zählpfeile kann beliebig angenommen werden. Hereinfließend wird dann positiv gezählt, herausfließend negativ. I1 Richtung des Stroms zwischen zwei Knoten muss konsistent sein. I2 Physikalisches Prinzip: Ladungserhaltung Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin I5 I4 I3 Maschenregel Maschenregel: „Die vorzeichenrichtige Summe aller Spannungen entlang einer Masche (Schleife) in einem Netzwerk ist immer 0V.“ U5 U1 U2 ∑U i = U1 + U2 + U3 + ... = 0 U4 U3 Die Richtung der Zählpfeile kann beliebig angenommen werden. In Laufrichtung wird dann positiv gezählt, gegen die Laufrichtung negativ. Physikalisches Prinzip: Energieerhaltung; bei konservativem Feld verschwindet Potentialdifferenz entlang geschlossener Kurve „Potentialdifferenz ist unabhängig vom Weg“ Elektrisches Feld und Gravitationsfeld sind konservative Felder Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Beispiel: Parallelschaltung von R Parallelschaltung von Ohm‘schen Widerständen Batteriestrom I0 teilt sich auf Widerstände auf (Knotenregel) I0 I0 = I1 + I2 + I3 U0 I1 I2 R1 An Widerständen liegt gleiche Spannung an U1=U2=U3=U0 Anwendung des Ohm‘sches Gesetz Ui=Ri·Ii I0 = ⎛ 1 U1 U2 U3 U0 U0 U0 1 1 ⎞ + + = + + = U0 ⋅ ⎜ + + ⎟ R1 R2 R3 R1 R2 R3 R R R 1 2 3 ⎠ ⎝144 244 3 1 = Rges Bei Parallelschaltung addieren sich Widerstände reziprok 1 1 =∑ Rges Ri Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin R2 I3 R3 Beispiel: Serienschaltung von R Serienschaltung von Ohm‘schen Widerständen U1 I0 −U0 = U1 + U2 + U3 R1 U0 R2 R3 U3 Gleicher Strom fließt durch alle Widerstände I1=I2=I3=I0 Anwendung des Ohm‘sches Gesetz Ui=Ri·Ii im folgenden nur Beträge −U0 = I1 ⋅ R1 + I2 ⋅ R2 + I3 ⋅ R3 = I0 ⋅ (R1 + R2 + R3 ) = I0 ⋅ Rges 144244 3 Rges Bei Serienschaltung addieren sich Widerstände Rges = ∑ Ri Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin U2 Leistung am Ohmschen Widerstand • elektrischer Strom verrichtet Arbeit am Ohmschen Widerstand: an jeder Ladung dq, die durch die Potentialdifferenz U über dem Widerstand R fließt, verrichtet das elektrische Feld die Arbeit: U + I R dW P= =U⋅I dt Es wird also die Leistung vom Feld und damit von Spannungsquelle erbracht. Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Messverfahren Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin Messverfahren Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin