Klausur „Grundlagen der Elektrotechnik III“ SS 2012, 02.07.2012

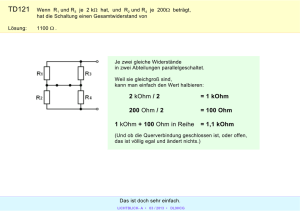
Name:
_______________________________
Matrikelnummer:
_______________________________
Punkte
Aufgabe
maximal
1
10
2
10
3
15
4
10
5
15
Gesamt
60
erreicht
Note:_______
Klausur „Grundlagen der Elektrotechnik III“ SS 2012, 02.07.2012
Hinweise:
1. Tragen Sie auf dieser Seite Ihren Namen, Vornamen und Ihre Matrikel-Nr. ein!
Dieses Blatt ist auf jeden Fall abzugeben! Versehen Sie bitte jede weitere
abgegebene Seite mit den gleichen Angaben!
2. Geben Sie Ihre Lösungswege und Berechnungsformel möglichst vollständig an.
Zahlenwerte ohne eindeutige Erklärung werden als Ergebnis nicht gewertet!
____________ Viel Erfolg! ______________
Aufgabe 1. Wechselstromgrundlagen (10 Punkte)
Eine periodisch zeitabhängige Spannung mit der im Bild 1 dargestellten Kurvenform hat
einen Scheitelwert von um=80 V (T – Periodendauer)
a) Wie groß ist der Gleichrichtwert | | der Spannung? (5 Punkte)
b) Welchen Effektivwert U hat die Spannung? (5 Punkte)
u
um
um/2
0
T/2
T
t
-um/2
Bild 1. Periodisch zeitabhängige Spannung für Aufgabe 1
Klausur ET3 // 02.07.2012 // Prof. S. Kovalev
Seite 1 von 3
Aufgabe 2. Wechselstromgrundlagen (10 Punkte)
Ein Kondensator mit der Kapazität C=1 µF liegt in Reihe mit einem ohmschen Widerstand
von R=100 Ohm. Die Anordnung soll nach Bild 2 über einen ohmschen Vorschaltwiderstand
RV mit einer Wechselspannungsquelle verbunden werden. Sie liefert eine Spannung von
U=200 V der Frequenz f=1000 Hz.
Welchen Wert muss der Widerstand RV haben, damit die an der Reihenschaltung von R und
C liegende Spannung URC =100 V wird?
I
RV
U
R
URC
C
Bild 2. Anlegen einer RC-Reihenschaltung über einen Vorschaltwiderstand an Wechselspannung
Aufgabe 3. Resonanz (15 Punkte)
In dem Reihenschwingkreis nach Bild 3 sind die Wirkwiderstände R1 und R2 sowie die
Induktivität L und die Kapazität C als gegeben anzusehen.
Es ist die Resonanzkreisfrequenz ωr der Schaltung in allgemeiner Form zu bestimmen.
L
R1
C
R2
Bild 3. Reihenschwingkreis zur Bestimmung der Resonanzkreisfrequenz
Klausur ET3 // 02.07.2012 // Prof. S. Kovalev
Seite 2 von 3
Aufgabe 4. Drehstromnetz (10 Punkte)
Ein Drehstromnetz mit der Außenleiterspannung U=400 V und der Frequenz f=50 Hz ist
nach Bild 4 durch drei gleiche, in Dreieck geschaltete RC-Reihenschaltungen belastet
(symmetrische Belastung). Jeder Wirkwiderstand hat den Wert R=100 Ohm und jeder
Kondensator die Kapazität C=40 µF.
a) Welcher Strom I fließt in jedem der drei Leiter des Drehstromnetzes? (5 Punkte)
b) Wie groß ist der Leistungsfaktor cosϕ der Schaltung? (2 Punkte)
c) Zeichnen Sie das Zeigerdiagramm (qualitativ) aller Spannungen und Ströme in der
Schaltung. (3 Punkte)
L1
R
C
C
L2
R
R
L3
C
Bild 4. Belastung eines Drehstromnetzes durch drei gleiche, in Dreieck geschaltete RC-Reihenschaltungen
Aufgabe 5. Schaltvorgänge (15 Punkte)
Die Schaltung nach Bild 5 enthält eine Induktivität L=1,0 H sowie die Wirkwiderstände
R1=3,0kOhm, R2=1,0 kOhm und R3=0,25 kOhm. Die Versorgungsspannung beträgt
U=100 V. Zum Zeitpunkt t=0 wird der vorhandene Schalter geschlossen.
a) Geben Sie eine DGL zur Berechnung des Verlaufs des Stromes durch die
Induktivität iL(t) als Formel an. (3 Punkte)
b) Lösen Sie diese DGL und geben Sie den Zeitverlauf des Stromes iL(t) als Formel mit
Zahlenwerten an. Stellen Sie den zeitlichen Verlauf iL(t) graphisch dar. (3 Punkte)
c) Transformieren Sie die Schaltung in Bildbereich und zeichnen Sie entsprechendes
ESB (Laplace – Transformation). (3 Punkte)
d) Geben Sie die Gleichung für iL(t) als Formel im Bildbereich an. (3 Punkte)
e) Transformieren Sie die Gleichung aus d) in den Zeitbereich zurück (LaplaceRücktransformation). (3 Punkte)
Korrespondenzen zur LaplaceR1
Transformation
iL(t)
S
L
U
R3
Originalfunktion
u(t), u(t<0)=0
R2
Bild 5. Schaltvorgang in einem ohmsch-induktiven Stromkreis
Klausur ET3 // 02.07.2012 // Prof. S. Kovalev
1
Bildfunktion
U(s)
1
1
Seite 3 von 3