Checkliste Sinus, Kosinus, Tangens
Werbung

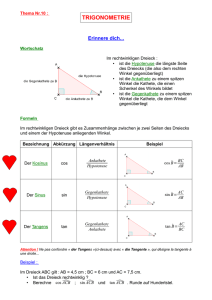
Checkliste Sinus, Kosinus, Tangens Nr. K1 K2 K3 K4 K5 K6 K7 K8 Kompetenz Ich kann.... in einem rechtwinkligen Dreieck Kathete, Gegenkathete und Hypotenuse bestimmen in einem rechtwinkligen Dreieck die Seitenverhältnisse sin, cos und tan aufstellen und fehlende Längen berechnen. mithilfe von Seitenverhältnissen fehlende Winkel berechnen. die oben beschriebenen Kompetenzen in Sachaufgaben anwenden in Körpern rechtwinklige Dreiecke nutzen, um Längen und Winkel zu berechnen. zeichnerische Lösungen im geeigneten Maßstab anfertigen. mit dem Sinus- und Kosinussatz fehlende Winkel und Seitenlängen in einem beliebigen Dreieck berechnen. mithilfe der Seitenverhältnisse im rechtwinkligen Dreieck und dem Sinus- und Kosinussatz Vermessungsaufgaben im Gelände durchführen, skizzieren und berechnen Aufgabe -- - o + ++ L. Aufgabe 1, 2, 3 und 4 Aufgabe 1, 2, 3 und 4 Aufgabe 5, 6 und 7 Aufgabe 8, 9, 10, 11, 12, 13 und 14 Aufgabe 15, 16 und 17 Aufgabe 18, 19 und 20 Aufgabe 21, 22, 23 und 24 Aufgabe 12 und 13; Aufgabe 25,26 und 27 Liebe Schülerin, lieber Schüler, arbeite zunächst das „Grundwissen“ zum Thema Trigonometrie durch. Danach bearbeite den Test 1 und werte ihn aus. Im Anschluss solltest du deine Kompetenzen mithilfe dieser Checkliste einschätzen. Nun musst du die Inhalte üben, die du nicht sicher beherrscht. Zum Schluss wird mit dem Test 2 dein Wissen getestet. Danach ist die Wiederholungseinheit abgeschlossen. Grundwissen Trigonometrie Seitenverhältnisse im rechtwinkligen Dreieck Dividiert man in einem rechtwinkligen Dreieck zwei Seitenlängen durcheinander, so erhält man eine Dezimalzahl (ohne Maßeinheit). Eine solche Zahl nennt man ein Seitenverhältnis. Diese Seitenverhältnisse sind für ähnliche Dreiecke gleich. Im rechtwinkligen Dreieck sind die Seitenverhältnisse in Abhängigkeit von den Winkeln (nicht dem 90° Winkel) mit Hilfe der Verhältnisse sin, cos und tan erfasst und mit dem Taschenrechner abrufbar. Die Seitenverhältnisse sin , cos und tan werden ausgehend von einem nicht 90° Winkel wie folgt definiert: sin (Winkel ) = Gegenkathete Hypotenuse cos (Winkel ) = Ankathete Hypotenuse tan (Winkel ) = Gegenkathete Ankathete Für das oben abgebildete Dreieck mit dem Winkel γ = 90° ergeben sich folgende Seitenverhältnisse: a c b cos(α ) = c a tan(α ) = b sin(α ) = b c a cos( β ) = c b tan( β ) = a sin( β ) = Man sollte sich die oben aufgeführten Seitenverhältnisse merken. Die links stehenden Formeln gelten nur für das oben abgebildete Dreieck mit der speziellen Lage des 90° Winkels. Berechnung von fehlenden Seiten im rechtwinkligen Dreieck: Sind in einem rechtwinkligen Dreieck drei voneinander unabhängige Größen gegeben, so kann das Dreieck konstruiert werden. Mithilfe der Trigonometrie können die fehlenden Seiten berechnet werden. Beispiel: Gegeben: c = 7cm, α = 65°, γ = 90° Berechnung von a: sin(α ) = a c a | ⋅7 7 sin(65°) ⋅ 7 = a a = 6,344 sin(65°) = Berechnung von b: cos(α ) = b c b | ⋅7 7 cos(65°) ⋅ 7 = b b = 2,96 cos(65°) = Bei der Arbeit mit dem Taschenrechner muss sichergestellt werden, dass der Taschenrechner auf Winkeleingabe (degree) eingestellt ist. Berechnung von fehlenden Winkeln im rechtwinkligen Dreieck: Die Winkelsumme im ebenen Dreieck beträgt 180°. Vie le fehlenden Winkel können mit dem Winkelsummensatz berechnet werden. Auch wenn von einem rechtwinkligen Dreieck nur der rechte Winkel und zwei Seiten gegeben sind, können Winkel berechnet werden. Der Taschenrechner liefert zu einem gegebenen Winkel ein entsprechendes Seitenverhältnis (Tasten sin, cos oder tan) und auch umgekehrt zu einem Seitenverhältnis (Dezimalzahl) einen Winkel (Tasten 2nd sin, 2nd cos oder 2nd tan ) Beispiel: b c 5,01 cos α = 7,45 cos α = 0,6724 cos α = α = 47,74° Berechnungen in ebenen Figuren: Viele geometrische Figuren können nur dann mithilfe der Trigonometrie berechnet werden, wenn man sie so zerlegt, dass rechtwinklige Dreiecke entstehen, in denen gerechnet werden kann (in denen drei Größen gegeben sind). Häufig werden die folgenden Figuren zerlegt: Gleichschenkliges Dreieck, gleichseitiges Dreieck, symmetrisches und unsymmetrisches Trapez, Parallelogramm, usw.. Auch das allgemeine Dreieck kann durch eine Höhe in zwei rechtwinklige Dreiecke zerlegt werden. Berechnungen im allgemeinen Dreieck: Im allgemeinen Dreieck können sin, cos und tan nicht angewandt werden. Hier kann mit dem Sinus- und dem Kosinussatz gerechnet werden. Sinussatz: sin α a = sin β b sin β b = sin γ c Zwei Seiten verhalten sich im beliebigen Dreieck wie die Sinus Werte. Kosinussatz: a 2 = b 2 + c 2 − 2bc ⋅ cos α b 2 = a 2 + c 2 − 2ac ⋅ cos β c 2 = a + b 2 − 2ab ⋅ cos γ Übungen zu den Kompetenzen K1 und K2 Aufgabe 1: Stelle für die dargestellten rechtwinkligen Dreiecke die Seitenverhältnisse sind, cos und tan für den eingezeichneten Winkel auf. a) b) c) Aufgabe 2: Berechne die gesuchten Größen. Fertige für jede Teilaufgabe eine Planungsskizze an. c = 7,8 cm a) Gegeben: α = 48° β = 90° b) Gegeben: γ = 72° γ = 90° Gesucht: b ? α = 90° c) Gegeben: b = 6,7 cm γ = 38° b = 12 cm Gesucht: a ? Gesucht: c und a ? Aufgabe 3: Berechne die fehlenden Seiten im rechtwinkligen Dreieck. Seite a Seite b Seite a Winkel α Winkel β Winkel γ 12,5 km 27,5 m 5,8 cm 47° 90° 27,4 m 4,35 dm 90° 72° 90° 45° 68,5° 90° 17° 90° Aufgabe 4: Berechne fehlende Seiten. Wähle selber eine sinnvolle Bezeichnung für die Ecken und Seiten und nutze die Variablen bei der Berechnung. Übungen zu den Kompetenzen K3 Aufgabe 5: Berechne die fehlenden Winkel in den gegebenen rechtwinkligen Dreiecken. Aufgabe 6: Berechne die fehlenden Seiten und Winkel in den folgenden rechtwinkligen Dreiecken. Fertige zu jeder Teilaufgabe eine entsprechende Planfigur an. Teilaufgabe Winkel α Winkel β Winkel γ Seite a Seite b Seite c a) 90° b) c) d) 90° 12,5 m 90° 90° 12 dm 5,8 dm 2,3 km 5,6 km 5,2 cm 10,2 m 3,4 cm Aufgabe 7: Fülle die Tabelle aus. Teilaufgabe Winkel sin α cos α tan α a) 30° b) c) d) e) 0,6 f) 0,22 0,33 2,56 0,95 Übungen zur Kompetenz K4 Aufgabe 8: Ein gleichseitiges Dreieck hat eine Seitenlänge von 7,5 cm. Berechne die Höhe und den Flächeninhalt dieses Dreiecks. Aufgabe 9: Ein gleichseitiges Dreieck hat eine Höhe von 10 cm. a) Fertige eine Skizze an. b) Berechne die Seitenlänge dieses gleichseitigen Dreiecks. c) Berechne den Flächeninhalt des Dreiecks. Aufgabe 10: In einem gleichschenkligen Dreieck sind die Seiten a=b=8,2 cm lang. Der Winkel γ beträgt 52°. a) Fertige eine Skizze dieses Dreiecks an. b) Berechne die Seite c. c) Berechne Umfang und Flächeninhalt dieses Dreiecks. Aufgabe 11: Ein senkrecht stehender Stab mit einer Länge von 2,80 m wirft einen Schatten von 2,50 m. a) Skizziere die Situation. b) Unter welchem Winkel treffen die Sonnenstrahlen auf der Erdoberfläche auf? Aufgabe 12: Wie breit ist der Fluss? Aufgabe 13: Um die Breite eines Flusses zu bestimmen, wird eine Hilfslinie AH festgelegt und gemessen. Mit einem Theodolit (Gerät zum genauen Messen von Winkeln) werden vom Standpunkt S aus die Winkel in Richtung A und B gemessen. Wie breit ist der Fluss? Aufgabe 14: Ein Kreis mit dem Radius von 7 cm enthält ein regelmäßiges Fünfeck. a) Fertige eine Skizze an. b) Berechne den Umfang und den Flächeninhalt. c) Mithilfe desselben Kreises wird ein regelmäßiges 10 Eck konstruiert. Jutta behauptet, der Flächeninhalt und der umfang dieses regelmäßiges 10 Ecks ist genauso groß wie der Umfang und der Flächeninhalt des regelmäßigen Fünfecks. Nimm zu dieser Meinung begründet Stellung. Übungen zur Kompetenz K5 Aufgabe 15: Ein Würfel besitzt eine Seitenlänge von 6 cm. Berechne die Länge der Raumdiagonalen und verdeutliche deine Berechnungen durch eine Skizze. 5 cm Aufgabe 16: Abgebildet ist das Netz einer Pyramide mit quadratischer Grundfläche. a) Berechne die Höhe der Seitenfläche hs b) Berechne die Körperhöhe der Pyramide hk. c) Berechne die Oberfläche der Pyramide (O). d) Berechne das Volumen der Pyramide (VP). Aufgabe 17: Das abgebildete Netz ergibt ein Prisma. a) Beschreibe den Körper, der durch den Zusammenbau des Netzes 2,8 cm entstehen kann. b) Berechne die eingezeichnete Höhe im Trapez. c) Berechne den Flächeninhalt der Rechtecke A,B und C. Ermittle dazu alle notwendigen Maße im Trapez. d) Berechne Oberfläche und Volumen des Körpers. 5 cm 4,2 cm 4,2 cm C A B 65 ° Trapez 45 ° 2,2 cm 7,2 cm Übungen zur Kompetenz K6 Aufgabe 18: Konstruiere das Dreieck mit c=12,5 m, b = 4,8 m und γ = 90° im Maßstab 1:100. Berechne alle nicht angegebenen Winkel und Seiten. Vergleiche die berechneten mit den gemessenen Werten. Aufgabe 19: a) Konstruiere ein regelmäßiges Fünfeck in einem Kreis mit einem Radius von 8 cm. b) Miss und berechne die Höhe h eines Dreiecks im regelmäßigen Fünfeck. c) Berechne den Flächeninhalt dieses regelmäßigen Fünfecks. Aufgabe 20: Ein Tennisball hat einen Durchmesser von 8 cm. Die Firma Tennisass stellt diese Bälle her und verkauft sie in einer Packung, in die sechs Bälle verpackt sind. Die Verpackung ist ein Prisma mit einem regelmäßigen Achteck als Grundfläche. a) Skizziere die Grundfläche einer solchen Verpackung. Die Tennisbälle sollen gerade hineinpassen. b) Konstruiere die Grundfläche einer 1:1 und führe alle notwendigen Berechnungen durch. Übungen zur Kompetenz K7 Aufgabe 21: Berechne die fehlenden Größen in den abgebildeten Dreiecken. C E H 4,1 cm 44 ° D 4,9 cm 97 ° 4,4 cm 109 ° 41 ° K F 38 ° B A 8 cm G Aufgabe 22: Berechne im spitzwinkligen Dreieck ABC die fehlenden Stücke. Fertige jeweils eine Planfigur an. a) a = 5,6cm b = 20,9cm γ = 82° b) a = 2,5cm b = 2,4cm β = 47° c) c = 5,6m b = 3,4m γ = 78° Aufgabe 23: Berechne die fehlenden Größen in den abgebildeten Dreiecken. E C 105 ° H 37 ° B 4,7 cm 4,1 cm 43 ° 6 cm K 116 ° 39 ° 8,4 cm A F D G Aufgabe 24: Berechne in den folgenden nicht rechtwinkligen Dreiecken die fehlenden Stücke. 1. b = 7cm; α = 123°; c = 12,5cm 2. a = 7 dm; b = 8,2dm; γ = 58° 3. c = 3,5cm; β = 78°; a = 9,5cm Übungen zur Kompetenz K8 Aufgabe 25: Ein Heißluftballon wird von zwei Standpunkten aus, die 245 m auseinander liegen, unter den Höhenwinkeln 38° und 52° angepeilt. Welche Höhe hat die Gondel des Heißluftballons über dem Gelände? Aufgabe 26: Um die Entfernung zwischen zwei Geländepunkte A und B zu bestimmen, wird im Geländepunkt B eine Messlatte aufgestellt. Am Theodoliten wird der Winkel α = 2,7° gemessen. Der Theodolit hat eine Standhöhe von 1,70 m. An der Messlatte wird die Entfernung BH = 2,25 m gemessen. Bestimme die horizontale Entfernung vom Punkt A nach B. 245 m Aufgabe 27: Um die Länge eines Sees zu bestimmen wird auf einer gradlinigen Straße eine Strecke AB = 340m abgesteckt. Von den Messpunkt A und B werden jeweils zwei Winkel zu den Peilpunkten C und D bestimmt. a) Trage die gemessenen Winkel in die Skizze ein. b) Zeichne die zu bestimmende Strecke CD ein c) Bestimme mit diesem Messungen die Länge des Sees in mehreren Rechenschritten D C BAD 32° BAC 92 ° ABC 28 ° ABD 95 ° A 340 m B Test 1: Aufgabe 1: Berechne die fehlenden Größen in den dargestellten Dreiecken. Aufgabe 2: Aufgabe 3: Test 2: Aufgabe 1: Berechne die fehlenden Größen in den dargestellten Dreiecken. Aufgabe 2: Aufgabe 3: