Aufgaben zur E-Lehre (Widerstand)

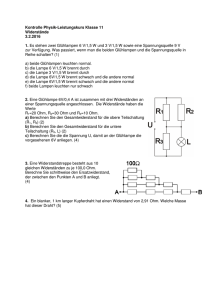
Aufgaben zur E-Lehre (Widerstand)
162. In einem alten Haus wurden die Aluminiumleitungen durch Kupferleitungen ersetzt;
insgesamt wurden 150 m Kabel verlegt. Jedes Kabel besteht aus einer Hin- und einer
Rückleitung und hat einen Querschnitt von 1,5 mm².
Um wie viel verkleinerte sich durch diese Veränderung der Widerstand der gesamten
Hausverkablung?
238. Die Widerstände zweier Leiter mit kreisförmigem Querschnitt, gleicher Länge und aus
gleichem Material verhalten sich wie 1:2. In welchem Verhältnis stehen die Massen der
beiden Leiter?
362. Ein Draht mit dem Widerstand R wird durch Ziehen auf die doppelte Länge gestreckt.
Wie groß ist der Widerstand des Drahtes nach dieser Tortour?
411. Wie groß ist die Windungszahl der Spule?
Zur Bestimmung dieser Größe wird bei einer angelegten Gleichspannung von 6,9 V ein
Strom von 46 mA gemessen. Der Draht der Spule besteht aus Kupfer und hat eine Masse
von 74 g. Die Spule hat einen Innendurchmesser von 2,1 cm, einen Außendurchmesser von
3,5 cm und ist 4,5 cm lang.
Hinweis zur Massebestimmung: Gemessen wurde die Masse der Spule, wie auf dem Bild zu
sehen. Von einer 2. Spule wurde die Masse des Spulenträgers bestimmt und vom ersten
Wert abgezogen.
176. Wie groß ist der Gesamtwiderstand zwischen den
Punkten A und B, wenn jeder Einzelwiderstand 3 Ω beträgt?
380. Welche Spannung darf maximal an der
Spannungsquelle eingestellt werden, damit
keine der Lampen kaputt gehen. Die
Widerstände der Lampen können als
konstant angenommen werden.
404. Ein einzelner Widerstand hat einen Wert
von 10,0 Ohm. Zu diesem Widerstand sollen
zwei gleiche Widerstände R geschaltet
werden, so dass sich der Gesamtwiderstand
zwischen den Punkten A und B nicht ändert.
Wie groß ist R?
405. Ein Strommesser hat einen Messwiderstand von 200 Ohm und einen Endausschlag
von 0,01 A. Durch einen zusätzlichen Widerstand soll der Messbereich auf 0,1 A erweitert
werden. Welchen Wert muss dieser Widerstand haben?
Lösungen
162.
geg.:
ρ Cu = 0,017 Ω ⋅ mm 2 ⋅ m −1
ges.:
∆R
ρ Al = 0,028 Ω ⋅ mm 2 ⋅ m −1
l = 300 m
A = 1,5 mm²
Lösung:
1. Widerstand der Aluminiumverkablung:
R = ρ⋅
l
A
R Al = 0,028 Ω ⋅ mm² ⋅ m −1 ⋅
300 m
1,5 mm²
R Al = 5,6 Ω
2. Widerstand der Kupferverkablung:
R = ρ⋅
l
A
R Cu = 0,017 Ω ⋅ mm² ⋅ m −1 ⋅
300 m
1,5 mm²
R Cu = 3,4 Ω
3. Änderung:
∆R = R Al − R Cu
∆R = 5,6 Ω − 3,4 Ω
∆R = 2,2 Ω
Antwort:
Der Widerstand verkleinert sich durch den Einsatz der Kupferleitung
um 2,2 Ohm.
238.
geg.:
l1 = l2
ges.:
ρ1 = ρ2
m1
m2
R1 1
=
R2 2
Lösung:
Da beide Leiter aus gleichem Material bestehen, haben sie auch die
gleichen Dichten. Die Dichte ist definiert:
ρ=
m
V
Damit verhalten sich die Massen der Leiter genau wie die Volumen
der Leiter:
m1 V1
=
m 2 V2
Das Volumen eines Körpers ist die Querschnittsfläche mal die
Länge des Körpers:
V = A ⋅l
Damit wird:
V1 A1 ⋅ l1
=
V2 A 2 ⋅ l 2
Da die Längen gleich sind, kann man kürzen:
V1 A1
=
V2 A 2
Nach dem Widerstandsgesetz:
R =ρ⋅
l
A
ist
R~
1
A
Also kann man schreiben:
V1 R 2
=
V2 R1
V1 2
=
V2 1
Und damit zum Schluss:
m1
=2
m2
m1 = 2 ⋅ m 2
Antwort:
Der Leiter mit dem kleinen Widerstand (Leiter 1) hat eine doppelt so
große Masse wie der Leiter mit dem großen Widerstand (Leiter 2)
362. Durch das Stecken wächst die Länge auf das Doppelte. Damit verdoppelt sich der
Widerstand erst mal.
Gleichzeitig wird der Draht aber noch dünner, so dass der Widerstand auch dadurch noch
ansteigt.
Für den Querschnitt des Drahtes gilt:
V = A ⋅ℓ
V
A=
ℓ
Da das Volumen gleich bleibt, die Länge sich aber verdoppelt, halbiert sich der Querschnitt.
Der Widerstand verdoppelt sich, wenn sich der Querschnitt halbiert.
Damit wird der Widerstand des Drahtes durch die Streckung vervierfacht.
411.
geg.:
ges.:
U = 6,9 V
N
I = 46mA
m = 74 g
di = 2,1cm
dA = 3,5cm
ℓ = 4,5cm
Lösungen:
Zur Bestimmung der Windungszahl der Spule muss als erstes die Länge des Drahtes
berechnet werden. Aus dieser Länge und dem Umfang einer Windung lässt sich dann
die gesuchte Windungszahl bestimmen.
1. Länge des Drahtes
Allgemein gilt das Widerstandsgesetz:
R = ρR ⋅
ℓ
A
In dieser Gleichung steckt schon die gesuchte Länge. Umgestellt heißt das:
ℓ=
R⋅ A
ρR
Der Widerstand lässt sich mit den gegeben Werten für Spannung und Stromstärke
bestimmen:
R=
U
I
und eingesetzt:
ℓ=
U⋅ A
I ⋅ ρR
Der Wert ρR ist der spezifische Widerstand für Kupfer und beträgt laut Wikipedia
ρR = 1,68 ⋅10 −2
Ω⋅ mm2
m
Die Querschnittsfläche A des Drahtes ist leider nicht bekannt. Lässt sie sich trotzdem
bestimmen? Ja!
Es gilt:
V =ℓ⋅A
Das Volumen ist die Länge des Drahtes mal die Querschnittsfläche.
Umgestellt:
A=
V
ℓ
Leider ist das Volumen noch unbekannt. Da man aber weiß, dass der Draht aus
Kupfer besteht und man zum Glück die masse bestimmt hat, kann man über die
Dichte das Volumen bestimmen:
m
V
m
V=
ρ
ρ=
Die Dichte lässt sich aus der Literatur o.ä. bestimmen
ρ = 8920
kg
m3
Die Querschnittsfläche ist dann
A=
m
ℓ ⋅ρ
Diese Gleichung wird in die Gleichung für die Länge eingesetzt:
ℓ=
U⋅m
I ⋅ ρR ⋅ ℓ ⋅ρ
ℓ2 =
U⋅m
I ⋅ ρR ⋅ρ
ℓ=
U⋅m
I ⋅ ρR ⋅ρ
Damit hat man eine schöne Gleichung für die Länge des Drahtes und kann diese
Berechnen:
ℓ=
U⋅ m
I ⋅ ρR ⋅ρ
6,9 V ⋅ 74 ⋅10−3 kg
kg
Ω⋅ m2
46 ⋅10 −3 A ⋅1,68 ⋅10 −8
⋅ 8920 3
m
m
ℓ = 272m
ℓ=
Die Einheitenbetrachtung ergibt wirklich Meter!
Das heißt, auf der Spule sind 272 m Draht. Wie viele Windungen sind das nun?
Eine Windung hat einen Umfang von
u = π⋅ d
Da für den Durchmesser der größte und der kleinste Wert gegeben sind, verwendet
man den Mittelwert, also 2,8 cm.
Der Umfang einer Windung ist demnach:
u = π⋅ 2,8 ⋅10−2 m
u = 8,8 ⋅10−2 m
also 8,8 cm.
Mit diesem Wert kann die Windungszahl berechnet werden.
ℓ
N=
d
272m
N=
8,8 ⋅10−2 m
N = 3090
Da die gegeben Größen maximal 2 gültige Stellen haben, kann die Windungszahl mit
3100 angeben werden.
N = 31⋅102
Antwort:
Auf der Spule sind 3100 Windungen.
176. Die Schaltung muss in einzelne, berechenbare Teile zerlegt und dafür die
Ersatzwiderstände berechnet werden.
1. Reihenschaltung der drei hinteren
Widerstände
2. Parallelschaltung
3. Reihenschaltung
4. Parallelschaltung
380.
geg.:
U1 = 3,6 V
ges.:
Ug
I1 = 0,24 A
U2 = 6,0 V
I2 = 0,1A
Lösungen:
Die Schaltung stellt eine Reihenschaltung von zwei Widerständen dar. Über
jedem Widerstand fällt ein Teil der Gesamtspannung ab.
Eine Glühlampe geht kaputt, wenn der Strom durch den Glühdraht zu groß
wird. In der Reihenschaltung ist der Strom an allen Stellen gleich. Damit darf
in dieser Schaltung ein maximaler Strom von 0,1 A fließen. Damit wird die
Lampe 2 nicht überlastet und Lampe 1 kann deutlich mehr vertragen.
Der Strom in einer Schaltung wird durch die anliegende Gesamtspannung und
den Gesamtwiderstand der Schaltung bestimmt.
Der Gesamtwiderstand lässt sich aus den gegeben Größen berechnen:
R g = R1 + R2
Die Einzelwiderstände sind
R1 =
U1
I1
R1 =
3,6 V
0,24 A
R1 = 15 Ω
Das heißt, bei einer Spannung von 3,6 V lässt diese Lampe durch ihren
Widerstand von 15 Ohm die angegebenen 0,24 A fließen.
Für die zweite Lampe wird der Widerstand ebenfalls berechnet:
R2 =
U2
I2
R2 =
6,0 V
0,1A
R2 = 60 Ω
Damit ist der Gesamtwiderstand der Schaltung 75 Ohm groß und die gesuchte
Spannung lässt sich berechnen:
U
I
Ug = Rg ⋅Ig
R=
Ug = 75 Ω⋅ 0,1A
Ug = 7,5 V
Antwort:
An der Spannungsquelle dürfen maximal 7,5 V eingestellt werden.
404. Der Gesamtwiderstand der Schaltung beträgt in beiden Fällen 10 Ohm. Es muss also
für die zweite Schaltung die Gleichung zur Berechnung des Gesamtwiderstandes aufgestellt
und daraus der gesuchte Widerstand berechnet werden.
Zur besseren Darstellung werden die
Widerstände bezeichnet: der 10 Ohm mit
R1, der unbekannte mit R1 und der
Gesamtwiderstand mit Rges.
Die beiden rechten Widerstände sind in
Reihe geschaltet und werden
zusammengefasst.
Damit ergibt sich für den Gesamtwiderstand:
Rges =
R2 ⋅ (R1 + R2 )
R2 + (R1 + R2 )
Als einziger unbekannter Widerstand ist R2
enthalten, nach dem umgestellt wird.
Rges =
R2 R1 + R22
R 2 + R1 + R2
Rges =
R 2 R1 + R22
2 ⋅ R2 + R1
Da der Gesamtwiderstand genau so groß wie der Widerstand R1 sein soll, kann man ihn
ersetzen:
R2 R1 + R22
R1 =
2 ⋅ R2 + R1
R1 ⋅ ( 2 ⋅ R2 + R1 ) = R2 R1 + R22
2R1R2 + R12 = R2 R1 + R22
Das sieht nach einer quadratischen Gleichung aus. Also Normalform:
0 = R2 R1 + R22 − 2R1R2 − R12
Ordnen:
0 = R22 − R1R2 − R12
Allgemeine Lösungsformel:
2
R
R 
R2 = 1 ±  1  + R12
2
 2 
Setzt man ein, erhält man einen negativen und damit sinnlosen Wert und 16,2 Ohm
405.
Der Widerstand muss parallel zum
Messgerät geschaltet werden. Damit wird
ein Teil des Stromes umgeleitet, der Strom
teilt sich auf zwei Teilströme auf. Es gilt:
Iges = IM + IR
Weiterhin ist die Spannung, die an dem
Messgerät und an dem gesuchten
Widerstand anliegt, gleich groß:
Uges = UM = UR
Durch die Aufgabenstellung sind vorgegeben:
Iges = 0,1A
IM = 0,01A
Damit ist klar, dass durch den Widerstand ein Strom von 0,09A fließen muss.
Wenn durch das Messgerät mit 200 Ohm widerstand ein Strom von 0,01 A fließen, muss
dafür eine bestimmte Spannung anliegen. Die lässt sich berechnen:
U
I
U = R ⋅I
R=
U = 200 Ω⋅ 0,01A
U= 2 V
Diese Spannung liegt auch an dem gesuchten Widerstand an. damit ist klar, dass durch den
Widerstand bei einer Spannung von 2 V ein Strom von 0,09 A fließen muss und der
Widerstandswert lässt sich berechnen:
R=
U
I
R=
2V
0,09 A
R = 22,2 Ω