Lösung Präsenzaufgabe

~B
~ =0
r
~ ⇥B
~ = µ0~j + µ0 ✏0 @t E
~
r
Theoretische Elektrodynamik
~E
~ = /✏0
r
~ ⇥E
~ = @t B
~
r
Wintersemester 2015/16, Universität Erlangen-Nürnberg, Prof. Dr. Florian Marquardt
Blatt 3: Präsenzaufgaben
Aufgabe 1: Zylinderkondensator
Wir betrachten einen zylindrischen Kondensator, bestehend aus zwei Zylindern der Länge L mit den Radien R1
und R2 > R1 , deren Achsen übereinstimmen. Berechnen Sie die Feldverteilung und das Potential für den Fall, dass
auf dem inneren Zylinder die Ladung +Q und auf dem äußeren die Ladung Q sitzt. Hinweis: Wir nehmen an,
dass L
R2 , und dass wir deshalb Feld und Potential angenähert so beschreiben können wie im Falle unendlich
langer Zylinder.
Bestimmen Sie nun: (i) Die elektrostatische Feldenergie U . (ii) Den Zusammenhang zwischen Ladung Q und Po2
tentialdi↵erenz V = 1
2 . Berechnen Sie die Kapazität C = Q/V . Zeigen Sie, dass U = CV /2.
Lösung:
~E
~ =
Zum Lösen muss über die Maxwell-Gleichung r
´
V
⇢
✏0 integriert
~ Ed
~ 3~r =
r
´
V
werden:
d3~r ✏⇢0
Die Linke Seite kann mit dem Satz von Gauß und Zylinderkoordinaten gelöst werden:
´
V
~ Ed
~ 3~r =
r
´
@V
´ L ´ 2⇡
~ A
~=
Ed
0
0
E(r) · rd'dz = 2⇡LrE(r)
Die rechte Seite beschreibt die im Volumen eingeschlossene Ladung und wird deshalb zu:
(
Q
´ 3 ⇢
R1 < r < R 2
✏0
d
~
r
=
✏0
V
sonst
0
Damit ergibt sich für das Feld:
Q
E(r) = 2⇡L✏
0r
(
1
0
R1 < r < R 2
sonst
Das Potential kann über die Beziehung:
E(r) =
@
@r
(r) ) (r) =
´
E(r)dr + C
berechnet werden. Es folgt:
(r) =
Fordert man dass
8
>
<
>
:
Q
2⇡L✏0
C1
ln(r) + C2
C3
r < R1
R1 < r < R 2
r > R2
stetig und im Unendlichen gegen 0 geht folgt für die Konstanten:
C3 = 0
C2 =
Q
2⇡L✏0
ln(R2 )
C1 =
Q
2⇡L✏0
2
ln( R
R1 )
Daraus folg:
(r) =
Q
2⇡L✏0
i)
8
R2
>
< ln( R1 )
ln( Rr2 )
>
:
0
r < R1
R1 < r < R 2
r > R2
Die Feldenergie berechnet sich aus dem Integral der Energiedichte über den gesamten Raum:
U=
´
u · d3 r =
✏0
2
´
2
[E(r)] d3 r = 2⇡L✏0 ·
Q2
(2⇡L✏0 )2
´ R2
1
R1 r 2
· rdr =
Q2
2⇡L✏0
ii)
V = (R1 )
(R2 ) = Q ·
1
R2
ln( )
2⇡L✏0
R1
|
{z
}
Es gilt:
V =
CV 2
2
=
Q2
2C
=
Q2
2
·
Q
C
1
2⇡L✏0
2
ln( R
R1 ) = U
C
1
2
ln( R
R1 )
Aufgabe 2: Gedankenexperiment
Wir stellen uns zwei Objekte (typische Festkörper) vom Volumen 1cm3 vor. Nehmen wir nun an, es würden 1 Promille aller Elektronen entfernt. Schätzen Sie ab, mit welcher Kraft sich die beiden Objekte nun (in einem Abstand
von 1m) abstoßen. Wenn man diese Kraft als Gewichtskraft eines Objektes auf der Erde realisieren will, welche
Masse muss es dann haben?
Lösung:
Wie viele Atome sind in 1cm3 ?
Typischer Atomradius = 1 · 10
10
m )VAtom = 10
30
m
3
) NAtom = 1024
In 1cm3 sind 1024 Atome, jedes Atom hat etwa 10 Elektronen ) Ne = 1025
Ein Atom hat eine Ladung von Qe = 1.6 · 10
19
C.
Entfernt man in jedem Würfel ein Promill der Elektronen hat man eine Ladung von:
Q = 10
3
· Ne · Qe ⇡ 103 C
Daraus ergibt sich eine Kraft von:
F =
Für
1
4⇡✏
1
4⇡✏0
·
Q2
r2
⇡ 1016 N
⇡ 1010 . Um diese als Gewichtskraft zu erreichen benötigt man eine Masse von:
m=
F
g
⇡ 1015 kg
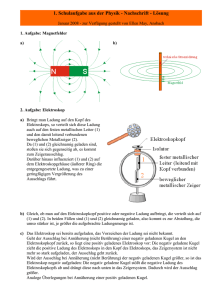
Aufgabe 3: Magnetfeld eines stromdurchflossenen Zylinders
Wir betrachten einen unendlich langen, massiven, leitenden Zylinder mit Radius R, der von einem Strom mit
~ und das Magnetfeld B
~ innerhalb
konstanter Stromdichte J~0 durchflossen wird. Berechnen Sie das Vektorpotential A
und außerhalb des Zylinders unter Benutzung der aus der Vorlesung bekannten Gleichung
~ = µ0 J~
r2 A
für magnetostatische Probleme.
Hinweis: Nutzen Sie die Symmetrie des Problems aus!
Überprüfen Sie das Ergebnis für das Magnetfeld explizit mit Hilfe der Maxwell-Gleichungen.
Lösung:
Wegen der Symmetrie ist es sinnvoll alle Rechnungen in Zylinderkoordinaten durchzuführen. Für den Strom gilt:
~ r) = J0 ⇥(R
J(~
r)êz
Das Vektorpotential zeigt demnach auch in z-Richtung, und ist nur von der Koordinate r abhängig. Somit vereinfacht
sich der Laplace Operator in Zylinderkoordinaten zu:
⇣
⌘
~
~
A(r)
= 1r @r r@r A(r)
= µ0 J0 ⇥(R r)êz
Für rR gilt:
~
@ A(r)
=
~
A(r)
=
µ0
2 J0 rêz
µ0
2
4 J0 r êz
+
~
a
r
+ ~a ln(r) + ~b
Für r>R gilt:
~
@ A(r)
=
~
c
r
~
A(r)
= ~c ln(r) + d~
~ = 0) 6= 1 und d~ = 0 o.B.d.A. Soll A(r)
~
Wir setzen ~a = 0 damit A(r
kontinuierlich und stetig sein folgt für ~bund ~c:
|~c| =
|~b|‘ =
µ0 2
2 R J0
µ0
2
2 J0 R
1
2
ln(R)
Für das Magnetfeld gilt:
~
~ ⇥ A(r)
~
B(r)
=r
=
@r
⇣
⌘
~
A(r)
· êz · ê' =
(
µ0
2 J0 rê'
~
|c|
r ê'
rR
r>R