Lösung 8

Physik I
Übung 8 - Lösungshinweise
Stefan Reutter
Moritz Kütt
Franz Fujara
WS 2011/12
Stand: 7. Februar 2012
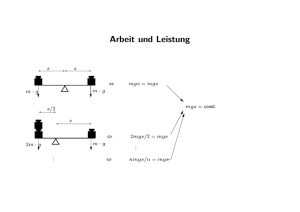
Aufgabe 1 Potentielle Energie
Schon in der letzten Übung wurde der Zusammenang F (~r) = −∇V (~r) ausgenutzt, um Kräfte
aus einem Potential zu bestimmen. Nach dem Gravitationsgesetz üben zwei Körper m und M
die Kraft F (r) = −G Mr 2m aufeinander aus (in Richtung des Abstandsvektors).
a) Bestimme daraus die Funktion für die potentielle Energie des Gravitationsfeldes (außerhalb
der Erdkugel, Erde ist Körper mit Masse M )
b) In der Vorlesung wurde auch oft eine potentielle Energie der Form E pot = mgh genutzt. Erläutere (in Worten), wie dieser Ausdruck mit dem in a) gefundenen Potential zusammenpasst.
c) Beschreibe den Zusammenhang auch mathematisch (Hinweis: Entwicklung).
Lösungshinweise:
d
V (r)
a) Aus F (~r) = −∇V (~r) kann man für ein kugelsymmetrisches Problem einfach F (r) = − dr
machen.
Dann ist
V (r) = −
R
F (r)d r =
R
m
G GM
dr
r2
V (r) = − G Mr m + C
In der Vorlesung wurde gesagt, dass die Integrationskonstante des Graviationspotentials üblicherweise so gewählt wird, dass das Potential im Unendlichen gegen 0 geht, damit ist
V (r) = −
GM m
r
b) Wie schon in a) erwähnt, kann man zunächst die Integrationskonstante frei wählen. Man
kann sie auch so wählen, das V (R er de ) = 0 ist. Das Potential, das so verschoben wurde, sieht aus
wie folgt:
V (r) = −
GM m
r
+
GM m
R
1
Es ist naheliegend, dass man das Potential in der Nähe der Erdoberfläche durch seine Tangente
gut beschreiben kann, man also ein lineares Potential näherungsweise verwenden kann (siehe
Skizze)
c) (Taylor-)Entwicklung um den Erdradius R, nur die ersten beiden Terme:
V (r 0 ) = V (R) + V 0 (R)(r 0 − R)
V (r 0 ) = − G MR m +
V (r 0 ) =
Nun kann man einfach
GM
R2
GMm 0
(r
R2
GMm
R
+
GMm 0
(r
R2
− R)
− R)
= g setzen, außerdem ist h = r 0 − R. Wenn man das ausnutzt, ist
V (h) = mgh
Aufgabe 2 Parabell
Nachdem der niedliche Pinscher Herr Schnuffelwuffel II. in einer früheren Übung nass geworden
ist, weil du ihn durch einen Fluss gehetzt hast, will er sich nun trocknen, indem er durch eine
Hundeföhnanlage fährt.
Die Hundeföhnanlage besteht aus einem (wasserfesten) Hundekorb, der entlang einer parabelförmigen Schiene hin und her fährt. Die Schiene hat die Form z(x) = kx 2 und das homogene
Schwerefeld der Erde wirkt in -z-Richtung. Du beobachtest, dass die x-Komponente von Schnuffelwuffels Bewegung eine harmonische Schwingung ausführt:
x(t) = Acos ωt
a) Berechne mit Hilfe des Gravitationspotentials die Kraft auf den Korb in x-Richtung
b) Berechne, wie groß die Kraft der Schiene auf das Hundekörbchen zu jedem Zeitpunkt sein
muss, damit es sich auf der Parabelbahn bewegt. Diese Kraft nennt sich eine Zwangskraft.
c) Berechne die Kreisfrequenz ω dieser Schwingung
Lösung:
a)
~
F~ = −∇φ
d
F x = − (mgkx 2 ) = −2mgkx
dx
Eine harmonische Schwingung tritt genau dann auf, wenn die Rückstellkraft linear entgegengesetzt der Auslenkung ist. Diese Kraft ist linear entgegengesetzt der Auslenkung, daher auch die
harmonische Schwingung
2
b) Die Idee hier ist einfach: Man nehme die vorgegebene Lösung und setze sie ins Newtonsche
Gesetz ein. Abzüglich der externen Kräfte ergeben sich die Zwangskräfte. In x-Richtung wirken
keine äußeren Kräfte, in z-Richtung muss die Gewichtskraft berücksichtigt werden. Zusätzlich
muss man für die z-Richtung vorher die Gleichung für die Schiene einsetzen.
In x-Richtung:
x(t) = Acos(ωt)
ẍ(t) = −Aω2 cos(ωt)
Z x = F x = mẍ(t) = −mAω2 cos(ωt) = −mω2 x
In z-Richtung:
z(t) = k (x(t))2 = kA2 cos2 (ωt)
ż(t) = −2kA2 ω sin(ωt) cos(ωt)
€
Š
z̈(t) = −2kA2 ω2 cos2 (ωt) − sin2 (ωt)
|
{z
}
=cos(2ωt)=2 cos2 (ωt)−1
Fz = mz̈(t) = Zz − mg
Zz = mg − 2mkA2 ω2 cos(2ωt)
c) ω =
p
2g k wie man durch Vergleichen der beiden Ergebnisse für F x sieht
Aufgabe 3 Snooker
Snooker pros know intuitively that their game is a good example for elastic collision. Before the
collision, the (white) cue ball is in motion while the target ball is at rest. After the collision, both
balls move. Calculate the possible angles between the velocities of both balls after the collision
for
a) mC = m T
b) mC 6= m T
Lösung:
Es gelten sowohl Impuls- als auch Energieerhaltung. Setze m1 = mC und m2 = m T
~p1 = ~p10 + ~p20
~p12
2m1
=
~p102
2m1
+
~p202
2m2
Wie in der Vorlesung definieren wir die Richtung von ~p1 als x-Achse, also ~p1 = p1~e x = m1 v 1~e x .
Aus der Impulserhaltung folgt dann
0
0
p1 = p1x
+ p2x
0 = p10 y + p20 y
3
Setzt man das in die Energieerhaltung ein ergibt sich
p12
m1
p12
m1
p12
m1
=
=
=
02
p1x
m1
€
Š2
0
p1 − p2x
m1
p12
m1
+
02
p2x
m1
−
Multipliziert man diese Gleichung mit µ =
+
+
p102y
+
m1
p202y
m1
+
0
2p1 p2x
m1
02
p2x
m2
02
p2x
+
p202y
m2
p202y
+
m2
m2
02
02
p2 y
p202y
p2x
+
+
+
m1
m2
m2
m1 m2
m1 +m2
0
02
02
− 2µv 1 p2x
+ p2x
0 = p1x
2
2
0
02
02
+ µv 1
− 2µv 1 p2x
+ p2x
µv 1 = p1x
Š2
€
2
0
02
− µv 1
+ p2x
µv 1 = p1x
Das ist eine Kreisgleichung, die erlaubten Werte für ~p2 liegen demnach auf einem Kreis mit
Radius µv 1 um den Punkt µv 1~e x im Impulsraum (siehe Skizzen unten).
a)
p'2
θ
θ'
p'1
p'2
p1
Sind die Massen gleich, ist µ = m2 , der Durchmesser des Kreises gleich p1 , und auf Grund des
Thalessatzes ergibt sich ein rechtwinkliges Dreieck. Die Energieerhaltung geht in den Satz des
Pythagoras über.
p12 = p102 + p202
Daher muss entweder ein rechter Winkel zwischen den beiden Geschwindigkeiten sein oder
(beim zentralen Stoß) ~p1 = 0 sein, was einem Winkel von 180◦ entspricht. Das ist beim Snooker
4
wie auch beim Billard auch, zumindest für harte Stöße, die in guter Näherung elastisch sind,
gut erfüllt.
b) Genau genommen muss man hier zwei Fälle unterscheiden, je nachdem, welche der beiden
m
Massen die größere ist. Wir betrachten zuerst den Fall m1 > m2 , dann ist µ < 21 und der
Durchmesser des Kreises kleiner p1
p'2
θ
θ'
p'1
p'2
p1
Die möglichen Winkel θ = π − θ 0 kann man sich geometrisch überlegen: θ 0 wird nicht kleiner
als 90◦ , weil ~p20 immer auf einem Kreis liegen muss, der zu klein ist, um einen spitzen Winkel
dort zuzulassen. Größer als 180◦ kann er natürlich ebenfalls nicht werden. Damit muss θ im
Bereich zwischen 0 und 90◦ liegen.
Genau anders herum ist es im Fall m1 < m2 . Dann ist der Kreis nämlich zu groß, um einen
stumpfen Winkel zuzulassen. θ muss also im Bereich zwischen 90◦ und 180◦ liegen.
p'2
θ'
p'2
θ
p'1
p1
5
Hausaufgabe 1 Kinder-Knet-Billard
Schon wieder werden der kleine Egon (m E = 40kg) und der kleine Manni (m M = 30kg) auf
dem Heimweg von fiesen Halbstarken gequält. Die Halbstarken haben Unmengen Knetmasse in
der Schule mitgehen lassen, und packen die beiden beinahe komplett darin ein. Dann tragen sie
beide in die große, schwerkraftfreie 
Schulturnhalle,
und schubsen sie beide
zu,
 so aufeinander


−2
5


 
dass Egon die Geschwindigkeit v~E =  3  m/s hat und Manni mit v~M =  −4  m/s auf ihn
3
3
zufliegt. Ihr Zusammenstoß findet vollkommen inelastisch statt.
a) Berechne die Geschwindigkeit von Egon und Manni nach dem Zusammenstoß im Turnhallensystem.
b) Wieviel Energie ist in innere Energie umgewandelt worden (Turnhallensystem)?
c) Berechne Egons und Mannis Geschwindigkeiten und kinetische Energien im Schwerpunktsystem.
d) Vergleiche jeweils im Turnhallensystem und im Schwerpunktsystem den Anteil der inneren
Energie an der Anfangsenergie.
Lösung:
a) Nach dem komplett inelastischen Stoß fliegt ein Egon-Manni-Klumpen mit einer Geschwindigkeit v~E M weiter.
m E v~E + m M v~M = (m E + m M )~
vEM
v~E M =
mE
v~
m E +m M E
+
mM
v~
m E +m M M

v~E M

2
 
=  0  m/s
3
b) Kinetische Energien vor dem Stoß von Egon und Manni:
Ek,E =
Ek,M =
1
m v 2 = 860 Nm
2 E E
1
m v 2 = 435 Nm
2 M M
Nach dem Stoß:
0
Ek,E
M = 455 Nm
Ek,E + Ek,M = Ei + Ek,E M
Ei = Ek,E + Ek,M − Ek,E M
Ei = 840 Nm
6
c) Für die Koordinatentransformation von Turnhallensystem (~x ) zu Schwerpunktsystem (~x 0 )
gilt:
~x 0 =
~x˙ 0 =
v~ 0 =
~x − ~x S P
~x˙ − ~x˙S P
v~ − v~S P
Im Falle von Egon und Manni ist v~SP = v~E M . Damit ergibt sich

v~E0 =
0
v~M
=
0
Ek,E
=
0
Ek,M =

3
 
 3  m/s
0


−4


 −4  m/s
0
360 Nm
480 Nm
d) Turnhallensystem:
Ei
Ea
=
Ek,E +Ek,M −Ek,E M
Ek,E +Ek,M
=
840 Nm
1295 Nm
= 65%
0
Im Schwerpunktsystem gilt: Ek,E
M = 0 Nm, damit auch:
Ei0
Ea0
= 100%
Hausaufgabe 2 Kinder-Pendel-Billard
Nachdem sie nun schon mehrere Male auf dem Nachhauseweg gequält wurden, suchen Egon und Manni
sich Verstärkung und rächen sich. Sie binden die drei
Halbstarken zusammen, und setzen sie an den Rand
der reibungsfreien Eisfläche (gemeinsame Masse mH =
300 kg. Es gibt eine Schaukel, auf die nun Manni klettert. Egon zieht ihn zurück, so dass Manni 2 m über
dem Haufen Halbstarker ist (siehe Zeichnung). Egon
lässt los, Manni schaukelt nach vorne und seine Füße
stoßen elastisch mit dem Haufen zusammen. Wie hoch
schwingt er nach dem Stoß zurück?
Das geht am einfachsten über verschiedene Energie- und Impulserhaltungsannahmen. Gesucht
ist Höhe nach dem Stoß (h0 ), die gegebene Höhe davor ist h = 2 m
7
Energieerhaltung für Mannis Geschwindigkeit beim Stoß
1
m v2
2 M M
m M gh =
p
vM =
2gh
Entweder weiß man aus der Vorlesung, dass
1
mH +m M
0
vM
=
(m M − mH )v M + 2mH v H )
mit v H = 0
m M −mH
v
mH +m M M
0
vM
=
Oder man leitet die Relation her:
Impulserhaltung für den Stoß
0
m M v M = mH v H0 + m M v M
v H0 =
mM
(v M
mH
0
− vM
)
Energieerhaltung für Stoß
1
m v2
2 M M
=
2
1
m v0
2 M M
2
0
m M (v M
− vM
) = mH v H0
2
2
0
0
m M (v M − v M
)(v M + v M
) = mH v H0
2
0
0
m M (v M − v M
)(v M + v M
)=
0
m M (v M + v M
)=
(m M +
0
vM
=
m2M
mH
m2M
mH
m2M
mH
+ 12 mH v H0
2
0 2
(v M − v M
)
0
(v M − v M
)
m2
0
)v M
= ( mM − m M )v M
H
m M −mH
v
mH +m M M
8
0
wieder h0
Nach der Herleitung bzw. der Nutzung der Vorlesungsformel kann man dann aus v M
berechnen:
2
1
m v0
2 M M
= m M gh0
h0 =
h =
0
h0 =
h0 =
0
vM
2
2g
m M −mH
mH +m M
2 v 2
M
2g
2 p2gh2
m M −mH
2g
mH +mM 2
m M −mH
h
mH +m M
h0 = 1, 34m
Hausaufgabe 3 Crash-Test
Ein Auto fährt mit einer Geschwindigkeit von 70 km/h an eine Wand. Am Ende des Aufpralls
steht es, jedoch wurde es um 35 cm eingedrückt. Berechne die Energie, die in Deformation
umgesetzt wird. Aus welcher Höhe müsste das Auto stürzen, damit beim Aufprall die gleiche
Energie umgesetzt wird? Nimm an, dass das Auto beim Crash eine konstante Beschleunigung
erfährt
Lösung:
W=
Zs2
F (s)ds =
s1
Zs2
ma br ems ds
s1
Wir nehmen an, dass das Zusammendrücken mit konstanter Beschleunigung geschieht, außerdem ist das Zusammendrücken quasi der Bremsweg s br ems = 35 cm.
!
0 = v (t) = v 0 − a br ems t
v
t = a0
!
s br ems = s(t) = 21 a br ems t 2
s br ems =
2
1 v0
2 a br ems
a br ems = 540m/s2
W=
s br
Zems
ma br ems ds = ma br ems s br ems
0
9
Bestimmung der Höhe über potentielle Energie
W = mgh
ma br ems s br ems = mgh
h=
a br ems · s br ems
g
h = 19, 3 m
10
Hausaufgabe 4 Männer. . .
Paul und Peter haben sich ein neues Männerspiel ausgedacht: Sie versuchen, sich auf einem zugefrorenen
Badesee gegenseitig möglichst heftig gegen eine Wand
zu schubsen. Genauer gesagt steht einer von ihnen still
und der andere schliddert möglichst schnell auf ihn
zu.
m2
v1
m1
Als die beiden gerade ihr Spiel für eine Weile unterbrochen haben, um sich bei einem Glühwein auf dem Weihnachtsmarkt aufzuwärmen, sabotiert der Fiese Füsiker Friedrich ihr Spiel,
indem er die Wand und die Jacken von Paul und Peter mit Superdotz™besprüht, sodass auf sie
gestoßene Leute energieerhaltend reflektiert werden.
Durch die Manipulation stößt Paul beim nächsten Versuch nicht einfach nur an die Wand, sondern wird auf Peter zurückgeworfen. Berechne, wie groß die Geschwindigkeiten der beiden sind,
bevor sie zum zweiten Mal aufeinander stoßen. Die Masse der Wand kann dabei als unendlich
groß angenommen werden
Lösung:
Beim Stoß mit der Wand wird einfach die Geschwindigkeit umgedreht. Sei ma = m1 und m b =
m2 . pai ist der Impuls von Masse a nach dem i-ten Stoß
1. Stoß:
pa0 = pa1 + p b1
2
pa0
=
2ma
2
pa1
2ma
+
(1)
p2b1
(2)
2m b
2. Stoß (mwand → ∞):
pa2 = pa1
(3)
p b2 = −p b1
(4)
Aus (2), (1):
0 = p b1
p b1 1 +
ma
mb
− 2pa0
p b1 = 0
p b1 =
2pa0
m
1 + ma
b
pa1 = pa0 1 −

2
1+
ma
mb
 ma
 = pa0 
mb
ma
mb
−1

+1

Die erste Lösung für p b1 ist hierbei unsinnig (kein Stoß).
11