Blatt 9

Sommersemester 2008
Lehrstuhl für Geometrie
Prof. Dr. H. Hähl
S. Poppitz
Neuntes Übungsblatt zur Veranstaltung
Synthetische Geometrie
⋆ Aufgabe 36
Stellen Sie sicher, dass Sie Aufgabe 28 vollständig bearbeitet haben.
⋆ Aufgabe 37 Geradenspiegelung
In der Situation von Aufgabe 28 sei a ∈ A \ {0} und G := La eine Gerade durch 0. Beschreiben
Sie die Spiegelung σ an der Geraden G mit Hilfe der algebraischen Strukturen auf A.
Hinweis: Zum Beispiel bietet sich eine der folgenden beiden Vorgehensweisen an:
(i) Jeder Punkt p ∈ A ist für geeignetes x ∈ A von der Form p = xa. In dieser Darstellung ist
der Bildpunkt von p leicht zu bestimmen. Hilfreich sind dabei auch die Erkenntnisse über
Orthogonalität (zum Beispiel aus Aufgabe 31).
(ii) Für jeden Punkt p 6∈ G gilt G = M p,σ (p) . Wertet man dies für zwei Punkte von G aus, erhält
man Gleichungen, aus denen man σ (p) gewinnen kann.
Aufgabe 38
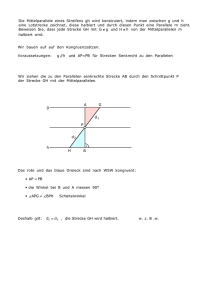
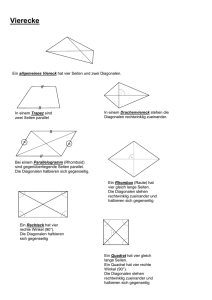
Gegeben ist eine präeuklidische Ebene. Ein nicht-ausgeartetes Viereck wird bezeichnet als
Raute, wenn alle vier Seiten kongruent sind,
Rechteck, wenn je zwei benachbarte Seiten orthogonal sind,
Quadrat, wenn je zwei benachbarte Seiten orthogonal und kongruent sind.
Sei V ein beliebiges Viereck. Weisen Sie die folgenden Aussagen nach:
(a) V ist genau dann eine Raute, wenn die Diagonalen von V orthogonal sind und einander
halbieren.
(b) V ist genau dann ein Rechteck, wenn die Diagonalen von V kongruent sind und einander
halbieren.
Hinweis: Die Parallele zu einer Diagonalen durch eine dritte Ecke kann helfen.
(c) V ist genau dann ein Quadrat, wenn die Diagonalen kongruent und orthogonal sind sowie
einander halbieren.
Zeigen Sie:
(d) Je zwei Durchmesser eines Kreises sind kongruent. (Durchmesser sind Strecken mit Endpunkten auf dem Kreis, die mit dem Mittelpunkt des Kreises inzidieren.)
(Bitte wenden)
Aufgabe 39 2–1-Teilungspunkt
Eine Strecke (a, b) einer präeuklidischen Ebene heißt nicht-ausgeartet, wenn a und b verschieden
sind. Ein von a verschiedener Punkt d heißt dann 2–1-Teilungspunkt der Strecke (a, b), wenn
b 6= mad und d der Mittelpunkt der Strecke (mad , b) ist.
(a) Begründen Sie, warum der 2–1-Teilungspunkt d der Strecke (a, b) auf der Geraden a ∨ b
liegt.
(b) Weisen Sie die Äquivalenz der folgenden Aussagen nach:
(i) Es gibt eine nicht-ausgeartete Strecke mit 2–1-Teilungspunkt.
(ii) Jede nicht-ausgeartete Strecke besitzt einen 2–1-Teilungspunkt.
Man sagt, eine solche präeuklidische Ebene hat nicht Charakteristik 3.
Aufgabe 40 Schwerpunkt eines Dreiecks
Es sei ∆ = (a, b, c) ein nicht-ausgeartetes Dreieck in einer präeuklidischen Ebene, die nicht Charakteristik 3 hat; es gibt also auf jeder Strecke einen 2–1-Teilungspunkt.
Zeigen Sie, dass die Schwerlinien a ∨ mbc , b ∨ mca und c ∨ mab des Dreiecks ∆ alle mit dem
2–1-Teilungspunkt s der Strecke (a, mbc ) inzidieren und dass dieser auch 2–1-Teilungspunkt der
Strecken (b, mca ) und (c, mab ) ist.
Hinweis: Untersucht man das Viereck (msa , mab , mbc , msc ), so kann man beweisen, dass es sich
um ein Parallelogramm handelt und dass s der Schnittpunkt der Diagonalen ist.