Huheey

Prof. Dr. Antonio Mezzetti
Laboratorium für Anorganische Chemie
ETH Hönggerberg
HCI H 235
Anorganische Chemie I
529-0121-00L
HS 2012
Inhalt
1.
Einleitung in die Koordinationschemie
2.
Symmetrie und Gruppentheorie
3.
Kristallfeldtheorie / Magnetische Eigenschaften
4.
MO LCAO (σ-Bindungen, π-Bindungen), π–Akzeptor-Liganden
5.
Elektronische Spektren
6.
Reaktionen, Kinetik und Mechanismen
Pflichtlektüre:
J. Huheey, E. Keiter, R. Keiter
Anorganische Chemie – Prinzipien von Struktur und Reaktivität
3. Auflage
de Gruyter
N.B. Ohne Huheey GEHT NIX!
Das Skript ist nur eine Foliensammlung!
Zusatzlektüren
–
M. J. Winter
d–Block Chemistry
Oxford University Press
–
L. H. Gade
Koordinationschemie
Wiley–VCH
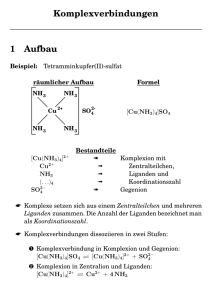
1. Einleitung in die Koordinationschemie
2
Inhalt
– Lernziele
– Definitionen: Ligand, dative Bindung, Komplex
– d-Orbitale
– Valenzelektronen and Oxidationszahl
– Elektronen-Buchhaltung
– Valenzstruktur-Theorie (Valence Bond, VB)
– Elektroneutralitätsprinzip und Kovalenz der koordinativen Bindung
– !-Donoren und !-Akzeptoren im VB-Ansatz
– Systematische Betrachtungen: Liganden, Koordinationsgeometrien, Nomenklatur
3
Was ist Anorganische Chemie?
Definitionsgemäss:
„Unbelebte Chemie“
Immer noch aktuell?
Eigentlich: die Chemie von 109 Elementen!
Wir werden das Problem reduzieren:
Chemie der Übergangsmetalle
(= Koordinationschemie)
Übergangsmetalle sind überall ...
In der organischen Chemie:
Metall-katalysierte Reaktionen
In der Biochemie:
In vielen Proteinen
In der Materialwissenschaft:
Magnetische / optische Eigenschaften
4
Lernziele
Erklärung der Struktur, der chemischen Bindung und der spektroskopischen Eigenschaften der
Komplexe der Übergangsmetalle:
Cl
Cl
CO
2–
Ni
Pt
Cl
8
d
Cl
OC
CO
CO
d10
Minimalistisch:
„Wir wollen d-Elektronen zählen können (auch in 20 Jahren noch!)“
Ernst:
„Wir wollen das Verhältnis zwischen d-Elektronenzahl des Metalls und
Struktur seiner Komplexe verstehen“
Dazu brauchen wir die Grundlagen der Bindungstheorie der Übergangsmetallkomplexe.
5
Die koordinative Bindung als roter Faden der Vorlesung
Die Bindung in Komplexen ist eine dative Bindung (koordinative Bindung).
Verglichen mit einer klassischen kovalenten Bindung hat eine koordinative Bindung die Eigenart,
das ganze Spektrum zwischen kovalent und ionisch abzudecken, was ihre Beschreibung wesentlich
komplizierter macht.
Damit ist gemeint, dass bestimmte koordinative Bindungen einen vorwiegenden kovalenten
Charakter besitzen, andere aber sich eher als ionische Bindungen verhalten.
Das Thema der Kovalenz der Bindung hat eine zentrale Bedeutung in der Komplexchemie, weil
die Natur der Bindung die Struktur und Reaktivität der Komplexe bestimmt.
Ein Beispiel davon ist die Geschwindigkeit der Substitutionen an oktaedrischen Komplexen, die
durch den Charakter der koordinativen Bindung (eher kovalent oder eher ionisch) entscheidend
beeinflusst wird.
In der Vorlesung werden wir diese Problematik ausführlich diskutieren und Konzepte entwickeln,
die uns bei der Deutung und Vorhersage der Natur der koordinativen Bindung helfen.
6
Metall + Liganden + Geometrie = Komplex
L
L
L
M
L
L
L
Metall: Übergangsmetalle (d-Block)
Ligand: Elektronen-Paar-Donor
Bindung: Lewis Donor–Akzeptor–Schema
Anzahl und räumliche Anordnung der Liganden bestimmen die
Koordinationsgeometrie (" Symmetrie!)
7
Der Anfang der Koordinationschemie
3+
NH3
H 3N
"CoCl3 · 6 NH3" + Ag+ (Überschuss) A 3 AgCl ?
Co
3 Cl–
NH3
H3 N
gelb
NH3
NH3
2+
NH3
H 3N
"CoCl3 · 5 NH3" + Ag+ (Überschuss) A 2 AgCl ?
Co
2 Cl–
NH3
H3N
purpur
Cl
NH3
+
L
"CoCl3 · 4 NH3 " + Ag+ (Überschuss) A 1 AgCl ?
2 Verbindungen:
die eine grün,
die andere violett
L
Cl
Co
Cl–
L
Cl
+
L
L
Co
Cl
Cl–
Cl
L
L
L
L = NH3
Alfred Werner (Nobelpreisträger für Chemie 1913)
8
Die Bindung in Komplexen:
Dative Bindung (Lewis-Modell):
H
H
+
B
H
N
H
H
H
B
H
H
H
H
N
H
H
Um dative Bindungen zu bilden, brauchen wir leere Orbitale.
H
H
M
+
N
M
H
H
N
H
Welche sind diese Orbitale?
(nd, (n+1)s und (n+1)p besitzen ähnliche Energien)
H
9
d-Orbitale: Durchdringung und Energie
10
Die Erste Übergangsreihe
11
Valenzelektronen und Oxidationszahl
12
Oxidationszahl
13
Elektronen-Buchhaltung
Wie viele Valenzelektronen gibt es im Bindungsschema des Komplexes?
Bsp:
[RhCl(CO)(PPh3)2]
(Rh(0) ist d9)
2 Methoden, dasselbe Resultat:
Geladen:
8 + 2 + 2 + 2 # 2 = 16 e–
Das Metall wird als Ion betrachtet, seine e–-Konfiguration angepasst.
Alle Liganden werden als 2-Elektronen-Donoren betrachtet. Ihre Ladung
wird angepasst (Cl· " Cl–).
Neutral:
9 + 1 + 2 + 2 # 2 = 16 e–
Das Metall wird als neutral angeschaut.
Alle Liganden werden als ungeladen betrachtet (Cl· bleibt Cl·).
14
Bindungsverhältnisse in Koordinationsverbindungen
3 Verschiedene Ansätze:
Valenzstruktur-Theorie (VB = Valence Bond), L. Pauling, ab 1930
Kristallfeld-Theorie
(CFT = Crystal Field Theory), 1950–1960
(erweitert als Ligandenfeld-Theorie)
Molekülorbital-Theorie (MO–LCAO), ab 1960
(Huheey, Kap. 11)
15
Valenzstruktur-Theorie
Ansatz:
Für Elemente der Hauptgruppen:
1. Hybridisierung
2. Paarung der einzeln besetzten Orbitale
Für Übergangsmetalle:
1. Die nd-Elektronen sind nichtbindend.
2. Die unbesetzten nd-Orbitale werden mit den (ebenfalls unbesetzten)
(n+1)s- und (n+1)p-Orbitalen hybridisiert.
3. Die Hybridorbitale bilden die dativen Bindungen zu den Liganden.
16
17
18
VB-Ansatz
Wenn Elektronenkonfiguration (Oxidationszustand) und Anzhal ungepaarten Elektronen (aus den magnetischen Eigenschaften) bekannt sind:
[PtCl4]2–
d8, diamagnetisch, nur gepaarte e–
[NiCl4]2–
d8, paramagnetisch, 2 ungepaarte e–
[Co(NH3)6]3+
d6, diamagnetisch, nur gepaarte e–
[CoF6]3–
d6, paramagnetisch, 4 ungepaarte e–
dann kann man die Koordinationsgeometrie voraussagen!
19
20
21
Dative Bindung und Elektroneutralitätsprinzip
Die dative Bindung verursacht den Aufbau negativer Ladung am Metall:
3+
OH2
H2O
H 2O
3
Fe
OH2
OH2
OH2
Pauling postuliert, dass soviele Elektronen transferiert werden, bis das Metall „elektroneutral“
(Ladung = 0) wird. Dies wird durch Resonanz-Strukturen wiedergegeben:
OH2
H 2O
3
Fe
H 2O
OH2
OH2
H 2O
OH2
H 2O
OH2
"kovalent"
3
OH2
50 % kovalent
OH2
50 % ionisch
Fe
OH2
Ladung(Fe) = 0
"ionisch"
Wenn beide Grenzstrukturen zu 50 % beitragen, dann ist die Ladung auf dem Fe-Atom gleich null!
22
"Kovalenz": Das allgegenwärtige Problem der Koordinationschemie
Durch die dative kovalente Bindung wird positive Ladung vom Metallion zum
Liganden transferiert.
Das Elektroneutralitätsprinzip diktiert, wie gross der kovalente Anteil der M–L-Bindung
sein muss, um die positive Ladung des Metallions vollständig zu neutralisieren:
[FeIII(OH2)6]3+
[FeII(OH2)6]2+
+1/2
+1/2
H2O
H2O
+1/2
OH2
Fe
+1/3
+1/2
+1/3
OH2
H2O
OH2
H2O
OH2 +1/2
+1/2
50 % kovalent
50 % ionisch
+1/3
OH2
Fe
+1/3
OH2
OH2
OH2
+1/3
+1/3
33 % kovalent
66 % ionisch
Konsequenz:
Die höhere Oxidationsstufe hat kovalentere Bindungen als die niedrigere!
23
Elektronegativität und Elektroneutralitätsprinzip
[Co(OH2)6]2+
Bsp.:
und
[Co(NH3)6]3+
Atom
!
Bindung
$!
Co
N
O
2.0
3.0
3.4
Co–N
Co–O
1.0
1.4
(! = Elektronegativität)
kovalenter
ionischer
Je grösser die Elektronegativitätdifferenz $!, desto ionischer die Bindung " Die Co–O-Bindung ist
ionischer als die Co–N-Bindung.
Deshalb bevorzugt das Co-Atom in [Co(OH2)6]n+ den niedrigeren Oxidationszustand, d. h. Co(II), in
dem die Co–O-Bindung den grössten ionischen Anteil hat:
2 [CoIII(OH2)6]3+ + H2O " 2 [CoII(OH2)6]2+ + 1/2 O2 + 2 H+
Umgekehrt ist [CoIII(NH3)6]3+ stabiler als [CoII(NH3)6]2+, weil der +3-Oxidationszustand den grössten
kovalenten Anteil hat als der +2-Oxidationszustand:
[CoII(NH3)6]2+ + H2O " [CoIII(NH3)6]3+ + OH– + 1/2 H2
24
Anwendung: Die Azidität der Aqua-Komplexe
[FeIII (OH2 )6]3+
[FeII(OH2)6]2+
+1/4
+1/4
+1/6
H
H
H
+1/2
H2O
H 2O
+1/2
O
Fe
+1/2
OH2
+1/3
H 2O
OH2
H2 O
OH2
+1/2
+1/2
+1/3
+1/6
O
H
Fe
+1/3
OH2
OH2
OH2
+1/3
+1/3
[FeIII(OH2)6]3+ + H2O
[FeIII(OH)(OH2)5]2+ + H3O+
pKa = 2.0
[FeII(OH2)6]2+ + H2O
[FeII(OH)(OH2)5]+ + H3O+
pKa = 7.0
25
M–OH2, M–OH und M=O
V(II):
[VII(OH2)6]2+
[VII(OH)(OH2)5]+ + H+
pKa ! 10
V(III):
[VIII(OH2)6]3+
[VIII(OH)(OH2)5]2+ + H+
pKa ! 2.9
V(IV):
[VIV(OH2)6]4+
– H+
nicht stabil
[VIVO(OH2)5]2+
[VIV(OH)(OH2)5]3+
– H+
[VIVO(OH)(OH2)4]+ + H+
[VIVO(OH2)5]2+
pKa ! 6.0
Der Oxo-Ligand (O2–) reagiert nicht als Oxid, die V–O-Bindung ist weitgehend kovalent!
Oxo-Komplexe sind nur in sehr hohen Oxidationszuständen stabil!
Beispiel: MnO4–
26
!-Donor-Liganden
V–O in [VO(OH2)5]2+ schreiben wir auch als V=O
Lewis-Begründung: V::O ist gleichwertig wie V2+ O2–.
Es gibt 4 bindende Elektronen, d. h. es handelt sich um eine Doppelbindung. Dies kann man mit dem
VB-Ansatz schlecht darstellen. Man braucht Orbitale (MO-LCAO, siehe später):
V
O
V
O
oder
V 2+ O
2–
Beide Bindungen sind L!M-dativ.
!-Donoren stabilisieren hohe Oxidationszustände (z. B. V(IV)).
27
Oxo-Liganden und Elektronenzahl
[CrVIO4]2–
Cr2+ O
2–
oder
Cr
O
der Oxo-Ligand ist ein
4-Elektronen-Donor!
gesamte e ––Zahl:
d0 + 4 # 4 e – (O2–) = 16 e –
d6 + 2 e – + 4 # 2 e – (O:-Diradikal) = 16 e –
„geladen“
„neutral“
[MoVICl4O2]2–
gesamte e ––Zahl:
d0 + 2 # 4 e – (O2–) + 4 # 2 = 16 e –
d6 + 2 e – + 2 # 2 e – (O:-Diradikal) + 4 # 1 = 16 e –
„geladen“
„neutral“
28
!-Akzeptor-Liganden
O
CO
Ni
OC
10
C
Ni
CO
CO
C
O
Ni
d
O
C
4
C
O
C
O
Aber:
Ni
Ni
C
C
O
Ni
C
O
O
die !-Bindung is L"M-dativ
die #-Bindung ist M"L-dativ
(Rückbindung)
!-Akzeptoren stabilisieren niedrige Oxidationszustände, z.B. Ni(0)
29
Einzähnige Liganden
30
Zweizähnige Liganden
Ligand
Donor
Example
Ligand
Donor
Example
31
Dreizähnige und Makrozyklische Liganden
Ligand
Donor
Example
Ligand
Donor
Example
32
33
34
2. Symmetrie und Gruppentheorie
36
Inhalt
– Symmetrieelemente und Symmetrieoperationen
– Punktsymmetrie und Punktgruppen
– Irreduzible Darstellungen und Charaktertafeln
– Reduzible Darstellungen
– Symmetrie und Kristallographie: Gitterpunkt, Gitter, Beugung
– Translationssymmetrie und Raumgruppen
(Huheey, Kap. 3)
37
Symmetrie Elemente und Symmetrieoperationen
Eine Symmetrieoperation (SO) überführt ein Molekül durch eine
– Drehung um eine Achse,
– Inversion an einem Punkt oder
– Spiegelung an einer Ebene (dem Symmetrieelement)
in eine Lage, die von der ursprünglicher Lage ununterscheidbar ist.
Wenn es in dem Molekül einen Punkt gibt, der bei allen Symmetrieoperationen räumlich unverändert (d. h. in Ruhe) bleibt, dann spricht man
von Punktsymmetrie.
38
Symmetrielement
Symmetrieoperation
– Spiegelebene (!):
Spiegelung des Gegenstandes an der Spiegelebene.
– Inversionszentrum (i)
Inversion des Gegenstandes durch das Inversionszentrum
– n-zählige Drehachsen (Cn)
Drehung um einen Winkel von 360 °/n (n / 2 – 6)
– Identität (E)
E = C2 " C2 (E = C22), E = C3 " C3 " C3 (E = C33)
– Drehspiegelung (Sn)
Drehung um 360° /n gefolgt von einer Spiegelung an einer
Ebene senkrecht zur Drehachse.
Bestimmte Symmetrieoperationen sind äquivalent:
S1 = !
S2 = i
39
40
41
Kombinationen von verschiedenen Cn-Drehachsen
42
Drehspiegelung (Sn)
43
Chiralität
Chiralität liegt vor, wenn ein Molekül mit seinem Spiegelbild nicht zur
Deckung gebracht werden kann.
Gleichwertig ist die Aussage, dass das Molekül keine Drehspiegelachse
haben darf.
Die Abwesenheit einer Spiegelebene ist dagegen kein ausreichendes
Kriterium, da ein Molekül durchaus eine Drehspiegelachse aber keine
Spiegelebene haben kann:
44
Punktgruppen (nach Schönflies)
Symmetrielemente kommen nicht in beliebigen Kombinationen vor. Das Vorliegen einiger
Symmetrieelemente (SE) bedingt die Anwesenheit anderer SE. Beispiel: Im H2O generieren zwei
zueinander senkrechten Spiegelebenen eine C2v-Achse:
Die Symmetrielemente:
C2, !v(xz), !v’(yz), E
„gehören zusammen“ und definieren die Punktgruppe C2v.
45
Punktgruppen geringer Symmetrie
C1
Cs
Ci
C1
E (Identität) ist das einzige Symmetrieelement
Cs
! (1 Spiegelebene) ist das einzige Symmetrieelement (ausser E)
Ci
i (Inversionszentrum) ist das einzige Symmetrieelement (ausser E)
46
Punktgruppen mit einer n-zähligen Drehachse Cn
– Nur 1 Dreachse:
Cn
C2
C3
– Eine horizontale* Spiegelebene (!h) zusätzlich zur Cn-Achse:
– n vertikale† Spiegelebenen (n
!v) zusätzlich zur Cn-Achse:
– Lineare Moleküle (ohne Inversionszentrum i) besitzen 1 C!-Achse:
C2h
C2v
C3v
C4v
C3
Cnh
Cnv
C!v
C!v
* Eine horizontale Spiegelebene (!h) ist senkrecht zur Hauptdrehachse (hier, Cn).
†
n Spiegelebenen, die sich in die Cn-Achse schneiden, nennt man vertikal (!v).
C!v
47
Diedergruppen – 1
– 1 Hauptdrehachse Cn
+ n C2 (senkrecht zur Hauptdrehachse Cn):
Dn
– 1 Hauptdrehachse Cn
+ n C2 (# zur Cn) + !v:
Dnh
– 1 Hauptdrehachse C!
+ ! C2 (# zur Cn):
D!h
D3
D!h:
D3h
D4h
D4h
D!h
D!h
D!h
Lineare zentrosymmetrische Moleküle weisen eine horizontale Spiegelebene und
unendlich viele C2-Achsen senkrecht zur Hauptdreachse C!
48
Diedergruppen – 2
– 1 Hauptdrehachse Cn
D3d
+ n C2 + n !d
D4d
(die den Winkel zwischen den C2- halbieren):
D2d
D6d
Dnd
49
Punktgruppen sehr hoher Symmetrie
Ih
Oh
[B12H12]2– (Ih)
Oh :
Oh
4 C3, 3 C4, 6 C2, 3 S4, 3 !h, 6 !d, i
Td : 4 C3, 3 C2, 3 S4, 6 !d
50
Fliessschema zur Ermittlung der Punktgruppe eines Moleküls
51
Irreduzible Darstellungen und Charaktertafeln
Die Symmetrieoperationen, die zu einer bestimmten Punktgruppen (PG) gehören, bilden eine
$ mathematische Gruppe.
Jede PG kann in Symmetriemuster zerlegt werden: $ irreduzible Darstellungen (ID)
Diese besagen, wie die Symmetrioperationen der PG die Eigenschaften des Moleküls verändern.
– Translation entlang der y-Achse:
B2
Bedeutung:
=
+1
–1
–1
+1 = symmetrisches Verhalten,
+1
(Charakteren)
–1 = antisymmetrisches Verhalten
x-Translation
B1
=
+1
–1
+1
–1
z-Translation
A1
=
+1
+1
+1
+1
Der Satz von 4 Charakteren (+1, –1, –1, +1) ist eine irreduzible Darstellung der Punktgruppe C2.
(Achsenwahl: höchstzählige Drehachse $ z-Achse. Die x-Achse ist # zur Molekülebene)
52
Irreduzible Darstellung
Die irreduzible Darstellung beschreibt nicht nur die Auswirkungen der C2v-Operationen auf eine
Translation in y-Richtung, sondern auf jede Funktion mit den Eigenschaften eines y-Vektors (z. B.
ein py-Orbital des Sauerstoffatoms).
!! y ist eine Basisfunktion für diese ID innerhalb der PG C2v !!
Nach den Prinzipien der Gruppentheorie ist die Zahl der irreduziblen Darstellungen einer PG gleich
der Anzahl der Klassen von Symmetrieoperationen, die diese PG charakterisieren. (Hier gibt es nur
ein Symmetrieoperation per Klasse.)
Wir erwarten 4 irreduzible Darstellungen für die PG C2v. Eine ID müssen wir noch finden ...
– Rotation um die C2-Achse:
A2
=
+1
+1
–1
–1
53
Charaktertafel (fasst diese Informationen in eine Matrix zusammen)
%
%
%
&
4 irreduzible Darstellungen (Mulliken-Symbole)
Dimension:
% 4 Klassen von Symmetrieoperationen
&
&
Basisfunktionen (R = Rotation)
A, B $ eindimensionale irreduzible Darstellung
Die Dimension hängt mit der mathematischen Herkunft der Charaktere zusammen: Jeder Charakter
ist die Summe der Diagonalelemente der Matrix, die die Symmetrieoperation beschreibt.
A
B
symmetrisches verhalten (+1) gegenüber der Hauptdrehachse (hier C2).
antisymmetrisches verhalten (–1) gegenüber der Hauptdrehachse.
1
2
symmetrisches verhalten (+1) gegenüber !v. *
antisymmetrisches verhalten (–1) gegenüber !v. *
* Oder, wenn vorhanden, gegenüber einer C2-Achse senkrecht zur Hauptdreachse, siehe unten.
54
[PtCl4]2–, D4h
55
Mulliken-Symbole
Eindimensionale irreduzible Darstellung:
A (symmetrisch zur höchstzähligen Drehachse)
B (antisymmetrisch zur höchstzähligen Drehachse)
Mehr als eine A bzw. B i. D.:
1 (symmetrisch gegenüber 2. Symmetrieelement)
2 (antisymmetrisch gegenüber 2. Symmetrieelement)
Inversionszentrum (i) vorhanden
g (gerade) (symmetrisch gegenüber i)
u (ungerade) (antisymmetrisch gegenüber i)
Horizontale Spiegelebene (!h)
' (symmetrisches Verhalten gegenüber !h)
'' (antisymmetrisches Verhalten gegenüber !h)
E
zweidimensionale irreduzible Darstellung:
C4 transformiert x in y und y in –x. Sein Charakter ist weder +1 noch –1, sondern 0,
weil die Summe der Diagonalelemente der Matrix ist = 0.
Die x- und y-Basisfunktionen transformieren als eine zweidimensionale (oder
„zweifach entartete“) Darstellung und werden als Paar tabelliert (x, y). Sie sind
innerhalb der D4h-PG untrennbar.
T
dreidimensionale irreduzible Darstellung.
(drei Vektoren werden durch die Symmetrieoperation ausgetauscht)
56
Reduzible Darstellungen "r
Bestimmte Eigenschaften eines Moleküls (Schwingungen, Orbitale, usw.) kann man als Vektoren
beschreiben. Wenn verschiedene Vektoren vorliegen, können diese in mehrere Arten miteinander
„kombiniert“ werden.
Allerdings kann die Zahl und Art dieser „Kombinationen“ nicht beliebig gewählt werden, sondern
werden durch die Symmetrie (Punktgruppe) des Moleküls bestimmt.
Diese Summe aller „Kombinationen“ nennt man reduzible Darstellung.
Jede reduzible Darstellung kann in irreduzible Darstellungen zerlegt werden.
Dazu verwendet man die
Reduktionsformel:
N = 1 $ " rx #" ix #n x
hx
Die Reduktionsformel gibt an, wie oft (N-mal) eine bestimmte irreduzible Darstellung in der zu
reduzierenden Darstellung enthalten ist.
h = Gesamtzahl der Symmetrieoperationen in der PG
" rx = Charakter der Operation x in der reduziblen D.
x
n = Anzahl von Operationen in der Klasse.
" ix = Charakter der Operation x in der irreduziblen D.
(Anwendungen der Reduktionsformel werden wir in Zusammenhang mit der MO-LCAO-Methode behandeln.)
3. Kristallfeld–Theorie
58
Inhalt
– Oktaedrische Komplexe
– Ligandenfeldstabilisierungsenergie (LSFE)
– High Spin / Low Spin
– Tetraedrische Komplexe
– Planar-quadratische Komplexe
– Feldaufspaltung (!o) und spektrochemische Reihe
– Anwendungen, Beispiele, Grenzen
– Magnetische Eigenschaften der d-Block-Komplexe
59
–
Geschichte: 1929 (Physik) " 1950 – 1960 (Chemie).
–
Ziel: UV-VIS-Spektren (Farbe!) / magnetische Eigenschaften der ÜM-Komplexe erklären.
–
Annahmen:
Die Wechselwirkung zwischen M und L ist elektrostatischer Natur, die Liganden werden als
Punktladungen betrachtet.
Die einzigen Orbitale, die betrachtet werden, sind die d-Orbitale.
–
Grenzen:
Weil nur d-Orbitale werden berücksichtigt, bleibt der grösste Teil der Bindungsenergie unerkannt.
Ionisches Modell " die Kovalenz der M–L-Bindung wird nicht beschrieben.
Nur #-Bindungen werden beschrieben!
(Huheey, Kap. 11, SS. 458–480)
60
Räumliche Anordnung der fünf d-Orbitale
61
Ligandenfeld-Effekte: Oktaeder-Symmetrie
62
Die unterschiedlichen M/L-Weschselwirkungen für t2g- und eg-Orbitale
63
Die Oh-Punktgruppe
Die Charaktertafel zeigt, dass es nur 2 Arten von d-Orbitalen gibt
(eg und t2g).
64
Elektrostatische Wechselwirkungen zwischen Liganden und Metall
Zuerst verteilen wir die 6 negativen Ladungen regelmässig auf der Oberfläche einer Kugel. Alle d-Orbitale werden gleichmässig
destabilisiert.
Dann konzentrieren wir die 6 Ladungen an die 6 Stellen, wo sich die Liganden befinden. Dadurch werden die t2g-Orbitale stabilisiert
(um 0.4 !o) und die eg-Orbitale destabilisiert (um 0.6 !o) (da der Schwerpunkt der Energie konstant bleibt).
65
[Ti(OH2)6]3+ und Elektronische Spektroskopie
d1-System: Das UV-VIS-Spektrum entsteht aus dem Übergang:
!max = 20 300 cm–1
"
t 2 g1eg0 ! t 2 g0 e1g
!E = 243 kJ mol–1 = ! o
66
Licht und Energie
Wellenzahl:
!=
! 1
=
c "
! (cm "1 ) =
10 7
# (nm)
Energie des Photons:
!E (kJ mol–1) = h ! NA = h ! c NA
Umrechnung:
!E (kJ mol–1) = 0.01197 (kJ mol–1 cm) $ ! (cm–1)
mit: h = 6.63 $ 10–34 J s
NA = 6.02 $ 1023
c = 3.00 $ 108 m s–1
67
Farbe und !o
t 2 g1eg0 ! t 2 g0 e1g
Gleicher Übergang, zwei unterschiedliche Komplexe:
! (cm–1)
[Ti(OH2)6]3+ (violett)
[ReF6] (farblos)
[Ti(OH2)6]3+
[ReF6]
20 300
32 500
% (nm)
492
308
!E (kJ mol–1)
243
388
LFSE pro Bindung
40.5 kJ mol–1
64.7 kJ mol–1
Die LFSE (200–400 kJ mol–1) ist immer kleiner als die Bindungsenergie, weil nur die nd-Orbitale in
Betracht gezogen wurden. Die (n+1)s- und (n+1)p-Orbitale werden nicht berücksichtigt!
Die KFT erklärt Farbe/Magnetismus, gibt aber nur qualitativ Auskunft über Bindungsenergien!
68
69
Ligandenfeld-Stabilisierungsenergie (LSFE oder CSFE)
d0
d1
d2
d3
70
„Low-Spin“ und „High-Spin“ Komplexe
d4: Zwei Möglichkeiten:
t2g4 eg0
t2g3 eg1
!O > P
starkes Ligandenfeld
!O < P
schwaches Ligandenfeld
Paarbildungsenergie P (oder Paarungsenergie)
Besteht aus zwei Beiträgen:
– Coulombsche
Abstossung (nimmt von 3d nach 5d ab, die Orbitale werden grösser)
– Verlust an Austauschenergie
(tritt ein, wenn Elektronen mit parallenen Spins gezwungen werden, antiparallele Spins anzunehmen)
71
Austauschenergie
Elektronen gleichen Spins weichen sich gegenseitig aus (Ausschliessungsprinzip von Pauli).
Als Folge davon schirmen diese die Kernladung füreinander jeweils weniger ab und die Anziehung
zwischen Kern und Elektronen ist stärker: dadurch wird die Gesamtenergie geringer.
Die zusätzliche Stabilität von Konfigurationen mit parallenen Spins ist die Austauschenergie Eex:
Eex = "
N(N – 1)
K
2
(K = Austauschenergie für 2 Elektronen)
Eex ist eine quadratische Funktion " sie nimmt mit der Zahl paralleler Spins rasch zu.
Halbgefüllten Unterschalen: maximale Zahl paralleler Spins " maximale Austauschenergie.
Der grösste Verlust an Austauschenergie für die d-Orbitale erfolgt, wenn bei einer d5-Konfiguration
zwei Elektronenpaare gebildet werden.
Daher weisen viele d5-Komplexe, z. B. von Mn(II) oder Fe(III), eine high-spin-Anordnung auf.
72
Paarbildungsenergien
PC = coulombsche Energie, Pex = Austauschenergie, Pges = gesamte Paarbildungsenergie
73
4
Low-Spin d –d
7
d4
d5
d6
d7
d5
d6
d7
High-Spin d4–d7
d4
74
8
LFSE für d –d
10
d8
d9
d 10
75
LFSE in Oh: Zusammenfassung
76
77
Wovon hängt die Grösse von ! ab?
1) Oxidationsstufe des Metalls
(! nimmt mit zunehmender OZ / Ladung zu)
2) Hauptquantenzahl n
(! nimmt mit zunehmender n zu)
3) Zahl der Liganden und Koordinationsgeometrie
(! nimmt mit zunehmender Ligandenzahl zu)
4) Art der Liganden: Spektrochemische Reihe
! nimmt in der Reihenfolge zu:
I– < Br– < S2– < SCN– < Cl– < N3– < F– < OH–, Harnstoff < O2–,
Oxalat < H2O < NCS– < py, NH3 < en < bipy, phen < NO2– <
< PR3 < CH3–, C6H5– < P(OR)3 < CN– < H– < CO < NO+
78
79
M- und L-Beiträge zu !
Der Wert von !o bei einem oktaedrischen Komplex kann nährungsweise durch ein Produkt zweier
unabhängiger Faktoren erhalten werden:
!o = f $ g
Die Grösse f gibt die Feldstärke eines Liganden relativ zu Wasser an (f(H2O) =1.00).
Der g-Faktor ist eine charakteristische Grösse des betreffenden Metallions.
80
In der Folge werden
Tetraedrische Komplexe
und
Planar-quadratische Komplexe
diskutiert.
81
Tetraeder-Symmetrie: Ligandenfeld-Effekte
82
Die Td-Punktgruppe
83
LFSE in Td
NB: !t =
4
9
!o
d0–d2
d0
d1
d2
84
LFSE in Td
d3
d4
d5
d6
d7
d8
d9
d 10
85
Tetragonale Symmetrie und planar-quadratische Komplexe
oktaedrisch
tetragonal
planar-quadratisch
86
Die D4h-Punktgruppe
87
88
89
Anwendungen der KFT
Die wichtigste Anwendung der KFT:
Magnetische Eigenschaften der Komplexe
Eine diamagnetische Substanz hat NUR gepaarte Elektronen.
N
Das externe Magnetfeld B0 ändert den Bahndrehimpuls der Elektronen und
induziert ein schwaches Feld, das gegen B0 ausgerichtet ist.
Das Magnetfeld ist schwächer in der Probe als ausserhalb.
µ
N
S
Universelle Eigenschaft der Materie (alle Substanzen haben gepaarte Elektronen).
S
Messung: Schwache Abstossung in einem inhomogenen magnetischen Feld:
90
Eine paramagnetische Substanz besitzt ungepaarte e– (Spin- und Bahnmoment).
Das externe Magnetfeld B0 orientiert den Spin- und Bahndrehimpuls parallel zum
B0. Das Magnetfeld ist stärker in der Probe als ausserhalb.
Das permanente (Spin- und Bahn-)Moment wird durch B0 ausgerichtet und in die
Region mit dem grössten Feld angezogen (Analogie zum elektrischen Dipol).
Der Paramagnetismus deckt den viel kleineren Diamagnetismus.
N
µ
S
N
Messung: Starke Anziehung in einem inhomogenen magnetischen Feld:
S
Komplexe der Übergangsmetalle mit ungepaarten Elektronen sind paramagnetisch.
Die Stärke des magnetischen Moments hängt von der Zahl der ungepaarten Elektronen ab.
Umgekehrt kann man aus Messungen des magnetischen Moments die Zahl der ungepaarten Elektronen
(und somit die Elektronenkonfiguration) des Komplexes ermitteln.
Die Grundlagen dieser Messungen werden in vereinfachter Form in der Folge erklärt.
91
Wird eine Substanz in ein magnetisches Feld gebracht,
ist das Feld B im Inneren der Probe:
grösser
kleiner
!H = B – H0 > 0
!H = B – H0 < 0
als das angelegte Feld H0
paramagnetisch
diamagnetisch
92
Intensität I der Magnetisierung (= magnetisches Moment pro Volumeneinheit)
4 & I = B – H0
4!
I
!=
H0
I
B
=
"1
H0 H0
Magnetische Suszeptibilität pro Volumeneinheit
paramagnetisch
! >0
diamagnetisch
! <0
Spezifische Suszeptibilität
Molare Suszeptibilität
/ H0
"M
"
" = #/$
($ = Dichte)
"M = " · M
(M = Molmasse)
93
Messung der Magnetisierung:
Faraday-Methode
Eine Probe der Masse m und der spezifischen Suszeptibilität " wird in ein inhomogenes Magnetfeld der
Stärke H0 gebracht.
!H
Der Gradient von H0 in z-Richtung ist
:
!z
'z
Auf die Probe wirkt die Kraft fz in der z-Richtung
fz = m · " · H0 · "$# ! H %'&
!z
94
Bestimmung der Molare Suszeptibilität "M
"!H %
fz = m · " · H0 · $
# ! z '&
Die Kraft ist die Differenz des Gewichtes der Probe g im Feld und ohne Feld:
fz = Gewichtmit Feld – Gewichtohne Feld
Der Wert des Gradients (%H/%z) wird nicht bestimmt.
Eichung mit einer Standard-Substanz mit bekanntem "M:
Aus:
fz
#"H &
= H0 %
$ " z ('
m!
ergibt sich:
fu
f
= s
mu ! u ms ! s
und somit "M der Probe als
!u =
ms ! s fu
f
=k u
fs mu
mu
Korrektur für den Diamagnetismus: siehe Huheey, S. 538.
(u = unbekannt, s = standard)
95
Die Magnetisierung auf der mikroskopischen Ebene
Ein Elektron besitzt einen Eigendrehimpuls (Spin) mit der Quantenzahl 1/2. Dieser Drehimpuls ist
Ursache eines magnetischen Moments µ:
µ= g
e!
2me
J(J + 1)
Kleinste Einheiten des magnetischen Momentes sind Bohr-Magnetone (BM):
1 BM = µ( =
e!
2me
e = Elementarladung, ! =
g = Landé-Aufspaltungsfaktor = 1+ J(J + 1) + S(S + 1) ! L(L + 1)
2J(J + 1)
h
, me = Elektronenmasse
2!
"
g = 2 wenn L = 0
Mit J = S (d.h. L = 0) erhält man:
µ=
e!
g S(S + 1)
2me
(S = Gesamtspinquantenzahl)
In BM ist es:
µ = 2 S(S + 1) (BM)
("spin-only"-Formel)
96
97
Magnetismus und Temperatur
In einer paramagnetischen Substanz werden die Momente durch das extern angelegte Feld orientiert.
Wird das Feld entfernt, verteilen sich die einzelnen Elektronenmomente durch die
statistisch in allen möglichen Richtungen.
thermische Bewegung
Die Probe weist makroskopisch kein magnetisches Moment auf, weil die Vektorsumme der Einzelmomente
verschwindet.
Konkurrenz
zwischen der ausrichtenden Wirkung des Feldes und der auf statistische
hinwirkenden thermischen Bewegung:
Gleichverteilung
Das magnetische Moment nimmt mit zunehmender Temperatur ab:
Curie-Verhalten:
Temperaturabhängigkeit von ", 1/" und µ eff:
98
Beziehung zwischen "M, µ und Zahl der ungepaarten Elektronen
Das molekulare magnetische Moment µ bestimmt "M durch:
"M = N
2 2
µ
3RT
(Curie-Gesetz)
(N = Avogadro-Zahl, R = Gaskonstante, T = absolute Temperatur)
Das Moment µ wird in Borschen Magnetons (BM) ausgedrückt (1 BM = e·h / 4 & m). Auflösung:
µ=
3RT
N2
"M
= 2.84
" M #T
99
„Spin-only Formula“
Aus
µ = g S(S + 1) (BM)
Mit
gElektron ) 2
erhält man:
n n
µ = 2 S(S + 1) = 4S(S + 1) = 4 !# + 1$& = n ( n + 2 )
2"2 %
µ = [n(n+2)]1/2 (BM)
(n = Zahl der ungepaarten Elektronen)
gilt NUR für komplexierte 3d-Ionen!
n
µ / BM
1
1.73
2
2.83
3
3.88
4
4.90
5
5.92
100
n und µ für 3d-Ionen
101
Anwendungen der KFT
Die KFT erklärt:
– Spektroskopische Eigenschaften (! und Ligandenfeld-Stärke)
– Magnetische Eigenschaften (Anzahl ungepaarter Elektronen)
– Thermodynamische Eigenschaften
(Gitterenergien, ionische Radien, Hydratationsenergien, E0)
– Kinetische Eigenschaften
(Geschwindigkeit der Substitutionsreaktionen)
von d-Block-Verbindungen
102
!o und !t: Zusammenfassung
NB:
10 Dq = !o
!t =
4
9
Dt
103
Gitterenergien von MX
2
(M = Ca – Zn)
Die Kationen M2+ besetzen Oktaederplätze in einem Gitter von X–-Anionen.
Da der Ionenradius von Ca2+ zum Zn2+ allmählich abnimmt, erwartet man ein allmähliches und
gleichmässiges Anwachsen in diese Richtung (dünn gezeichnete Kurve).
Die experimentelle Kurve zeigt den Effekt der LSFE in diesen high-spin oktaedrischen Systemen.
104
Ionische Radien
105
Hydratationsenthalpien von [M(OH ) ]
+
2 6
(M = Ca – Zn)
M (s) + 6 H2O + 2 H+ (aq)
" [M(H2O)6]2+ (aq) + H2 (g)
M2+ (g) + 2 e–
" M (s)
2+
+
–
M (g) + 6 H2O (l) (+2 H (aq) + 2 e ) " [M(H2O)6]2+ (aq) (+ H2 (g))
+!Hformation
–!Hvap + ion
!Hhydration
(die Standardbildungsenthalpie für H+ (aq) ist = 0)
106
0
Standard Redox-Potenziale E
[Co(H2O)6]2+ " [Co(H2O)6]3+ + e–
E0 = –1.83 V
[Co(ox)3]4– " [Co(ox)6]3– + e–
E0 = –0.57 V
[Co(phen)3]2+ " [Co(phen)3]3+ + e–
E0 = –0.42 V
[Co(edta)]2– " [Co(edta)]– + e–
E0 = –0.37 V
[Co(en)3]2+ " [Co(en)3]3+ + e–
E0 = –0.18 V
[Co(NH3)6]2+ " [Co(NH3)6]3+ + e–
E0 = –0.11 V
[Co(CN)5(H2O)]3– + CN– " [Co(CN)6]3– + H2O + e–
E0 = +0.83 V
107
Substitutionsreaktionen an oktaedrischen Komplexen
[M(H2O)6]n+ + H2O*
inerte Komplexe
d3, l.s. d4–6
Ladungsdichte q2/r
($ 10–28 C2 m–1)
[M(H2O*)(H2O)5]n+ + H2O
labile Komplexe
d1,d2/h.s. d4, d5, d6/d7, d9, d10
d8
34
Al3+
17
Be2+
10 2
Mn2+ Na+
108
Geschwindigkeit der Substitutionsreaktionen
Effekt der elektronenkonfiguration dn in oktaedrischen* Komplexen
Langsame Reaktionen (inerte Komplexe): d3, low spin d4–6
Schnelle Reaktionen
Erklärung:
(+ strong-field d8, pl. quadr.)
(Grenzfall: weak-field d8, okt.)
(labile Komplexe): d0, d1, d2, high spin d4–7, d9 und d10
Inert sind Komplexe, die im Übergangszustand LFSE verlieren!
109
Beispiele
[Fe(OH2)6]3+ + Cl– " [FeCl(OH2)5]2+ + H2O
gelb
[FeCl(OH2)5]2+ + PO43– " [Fe(PO4)(OH2)5] + Cl–
farblos
[Fe(PO4)(OH2)5] + SCN– " [Fe(SCN)(OH2)5]2+ + PO43–
rot
[Fe(SCN)(OH2)5]2+ + F– " [FeF(OH2)5]2+ + SCN–
farblos
Für alle diese Reaktionen gilt:
Reaktionszeit ! 1 min
"
alle labile h.s.-Fe(III)-Komplexe
Der Co(III)-Komplex [Co(NH3)6]3+ im Gegensatz:
[Co(NH3)6]3+ + 6 H3O+
[Co(OH2)6]3+ + 6 NH3
ist nicht stabil in saurer Lösung, reagiert aber sehr langsam:
!G° < 0
inert
110
111
Die Grenzen der KFT
Die Koordinationsbindung hat einen kovalenten Anteil, dessen Grösse von
den Liganden und vom Metall (Art, Oxidationszustand) abhängt.
Einige Hinweise auf die kovalente Komponente der Koordinations-Bdg:
–
Der nephelauxetische Effekt (siehe später, Elektronische Spektren der ÜM-Kompl.):
Die e––e–-Abstossung (Paarbildungsenergie) in Komplexen ist schwächer als im freien Ion.
Erklärung: Die Orbitale des Komplexen sind grösser als die vom freien Ion. Dies weist auf die
Überlappung der M- und L-Orbitale (Kovalenz!) hin.
–
NMR- und ESR-Kopplungskonstanten
Das Metallatom überträgt magnetische Kopplung zwischen magnetischen Kernen (z.B. H, P, F).
Erklärung: Die Spin-Information wird durch Elektronen weitergegeben, die sich im gleichen
Orbital befinden (Kovalenz!) (H*'M'*P).
112
Die KFT kann den kovalenten Anteil der Bindung nicht beschreiben!
4. MO–LCAO (Molekülorbital-Theorie)
114
Inhalt
– MO–LCAO und Gruppentheorie: Eine Einführung
– Oktaedrische Komplexe: !- und "-Bindung
– Tetraedrische Komplexe: !-Bindungen
– "-Donoren und "-Akzeptoren (CO, N2, NO+, C2H4, O2, Phosphine, Phosphite, H2)
– Quadratisch planare Komplexe: !- und "-Bindungen (als Übung)
(Huheey, Kap. 11, S. 480 – 504)
115
MO–LCAO und Gruppentheorie: Eine Einführung
Wie im Kapitel 2 besprochen, beschreibt die Charaktertafel die Symmetrieelemente einer Punktgruppe und das
Verhalten der Eigenschaften eines Objekts dieser Symmetrie gegenüber den Symmetrieoperationen.
Zusätzlich zeigt sie, dass die Eigenschaften des Objekts ("reduzible Darstellung") durch Zerlegung in einfachere
"Komponenten" ("irreduzible") vereinfacht beschrieben werden können.
Als Beispiel nehmen wir einen (x,y,z)-Vektor in der C2v-Punktgruppe:
Für jede einzelne Symmetrieoperation existiert eine Matrix, die die Koordinaten des Vektors transformiert:
Folgende Matrizen beschreiben den Effekt der Symmetrieoperationen der C2v-Punktgruppe auf unseren (x,y,z)-Vektor
(unten links):
Es fällt auf, dass alle Symmetrieoperationen durch Diagonalmatrizen beschrieben werden! Somit kann man sie
vereinfacht durch ihre Spuren (traces) darstellen (oben rechts). Dass alle Elemente ausserhalb der Diagonale gleich
Null sind suggeriert eine wesentlich wichtigere Vereinfachung (nächste Folie).
116
Reduzible und Irreduzible Darstellungen
Da alle Elemente ausserhalb der Diagonale gleich Null sind, können wir den (x,y,z)-Vektor in seine Komponenten
zerlegen:
Somit erhält man drei eindimensionale 1#1-Matrizen. Diese entsprechen den Charakteren der x-, y- und zKomponenten des (x,y,z)-Vektors in den jeweiligen irreduziblen Darstellungen B1, B2 und A1:
Wir haben den (x,y,z)-Vektor in seine x-, y- und z-Komponenten zerlegt! In der Sprache der Gruppentheorie sagt man,
dass die reduzible Darstellung !m die Summe der B1-, B2- und A1-irreduziblen Darstellungen ist:
!m = B1 + B2 + A1
Die Charaktere der reduziblen Darstellung sind die Summe der Charaktere der jeweiligen irreduziblen Darstellungen:
117
Reduktion
Die Zerlegung (Reduktion) des (x,y,z)-Vektors in seine x-, y- und z-Komponenten kann systematisch durchgeführt
werden. Voraussetzung ist, dass die Charaktere der reduziblen Darstellung bekannt sind (siehe oben):
!m
3
–1
1
1
Dazu wird die Reduktionsformel verwendet. Für die reduzible Darstellung !m gilt:
N = 1 # !rx "!ix "n x
h x
n x = Anzahl von Operationen in der Klasse.
" ix = Charakter der Operation x in der irreduziblen D.
h = Gesamtzahl der Symmetrieoperationen in der PG
" rx = Charakter der Operation x in der reduziblen D.
1
[(3 ! 1! 1) " (1! 1! 1) + (1! 1! 1) + (1! 1! 1)] = 1
4
1
N(A2 ) = [(3 ! 1! 1) " (1! 1! 1) " (1! 1! 1) " (1! 1! 1)] = 0
4
1
N(B1 ) = [(3 ! 1! 1) + (1! 1! 1) + (1! 1! 1) " (1! 1! 1)] = 1
4
1
N(B2 ) = [(3 ! 1! 1) + (1! 1! 1) " (1! 1! 1) + (1! 1! 1)] = 1
4
N(A1 ) =
und somit !m = A1 + B1 + B2
wie oben gezeigt.
118
C4-Rotation in C4v (Entartung)
Als zweites Beispiel betrachte man einen (x,y,z)-Vektor in der C4v-Punktgruppe:
Wie transformiert die C4-Achse den (x,y,z)-Vektor? Da die C4-Achse auf der z-Achse liegt, lässt eine 90°-Rotation um
die C4-Achse die z-Komponente des Vektors unverändert. Eine 90°-Rotation um die C4-Achse im Uhrzeigersinn
transformiert die x-und y-Komponenten gemäss:
x $ –y
y$x
Somit ist die Rotationsmatrix:
0 !1 0
1 0 0
0 0 1
Beweis:
" 0 !1 0 % ! x $ " !y %
$1 0 0 ' # y & = $ x '
$
'# & $ '
$# 0 0 1 '& "# z &% $# z '&
119
Die Rotationsmatrix enthält Elemente ausserhalb der Diagonale, die nicht gleich Null sind (siehe unten links). Diese
Elemente betreffen die x-und y-Komponenten. Man sagt, dass ein .x-Vektor und ein y-Vektor "zusammen" oder
"gemeinsam" transformieren oder, dass sie "entartet" sind. Somit kann ein (x,y,z)-Vektor nur in seine (x,y)- und zKomponenten zerlegt werden(siehe unten rechts):
0 !1 0
1 0 0
0 0 1
0 !1
1 0
0
0
0 0
1
Man beachte, dass die Spur der 2#2 (x,y)-Rotationsmatrix für die C4-Achse gleich Null ist. Dementsprechend ist in
der C4v-Charaktertafel der Charakter für die C4-Achse = 0:
$
Ein (x,y,z)-Vektor kann in der C4v-Punktgruppe in die z-Komponente (A1) und in eine x,y-Komponente (E) zerlegt
werden. Die x- und y-Komponenten können nicht getrennt werden, weil sie zusammen transformieren. Sie gehören
zur zweifach entarteten irreduziblen Darstellung E.
Somit kann man den (x,y,z)-Vektor in folgenden Komponenten zerlegen:
!m = A1 + E
120
Komplexere Punktgruppen: C3v
Betrachten wir die C3v-Punktgruppe, die folgende Symmetrieoperationen enthält:
Die Identität transformiert jeden Vektor in sich selbst. Somit lautet die entsprechende Matrix:
! 1 0 0 $! x $ ! x $
#
&#
& #
&
# 0 1 0 &# y & = # y &
# 0 0 1 &# z & # z &
"
%"
% "
%
Für die Spiegelung durch die (x,z)-Spiegelebene gilt:
" 1 0 0 %" x % " x %
$
'$
' $
'
$ 0 !1 0 '$ y ' = $ !y '
$ 0 0 1 '$ z ' $ z '
#
&#
& #
&
Die Situation für die C3-Rotation ist komplizierter (siehe unten).
121
Allgemeine Rotationsmatrix für eine Rotation um die z-Achse
Die Rotation eines (x,y,z)-Vektors um die z-Achse lässt die z-Komponente des Vektors unverändert. Somit lautet die
Matrix:
! ? ? 0 $
#
&
# ? ? 0 &
# 0 0 1 &
"
%
Betrachten wir einen Vektor des Betrags r, der einen Winkel % mit der x-Achse bildet (Polarkoordinaten).
Die Koordinaten vor der Rotation (x,y) sind:
y
x = r cos %
y = r sin %
Rotation
und werden durch die Rotation um einen Winkel & in die neuen Koordinaten (x', y')
umgewandelt:
"
x' = r cos (% + &) = r cos % cos & – r sin % sin & = x cos & – y sin &
y' = r sin (% + &) = r sin % cos & + r cos % sin & = y cos & + x sin &
Kurz:
!
x
x' = x cos & – y sin &
y' = x sin & + y cos &
In Matrixform:
" cos!
$
$ sin !
$ 0
#
!sin !
cos!
0
%" x % " x ' %
'$
' $
'
'$ y ' = $ y' '
'$ z ' $ z' '
&#
& #
&
0
0
1
(Für die Rotation im Uhrzeigersinn muss man die Vorzeichen des sin &-Terms umkehren.)
122
Die C3-Rotationsmatrix
Somit lautet die 120°-Rotation eines (x,y,z)-Vektors um die C3-Achse (die z-Achse):
"
$ ! 12
$
$ 3
2
$
$ 0
$
#
! 3
!1
0
2
2
%
0 '
'
0 '
'
1 '
'
&
Die Zusammenfassung der drei 3#3-Matrizen für die E-, C3- und !v-Symmetrieoperationen auf den Vektor r lautet:
Der Vektor r kann in seine (x,y)- und z-Komponenten zerlegt werden, nicht aber weiter, weil die C3-Symmetrieoperation die x- und y-Komponenten vermischt. Die Matrizen können in 2#2- und 1#1-Matrizen diagonalisiert
werden:
123
C3v: Matrizen und Charaktere der irreduziblen Darstellungen
Die Charaktere der irreduziblen Darstellungen erhalten wir als Summe der Diagonalelemente der Matrizen:
und somit:
Das (x,y)-Symbol in der dritten Zeile der Charaktertafel bedeutet, dass die x- und y-Richtungen in C3v äquivalent und
ununterscheidbar sind:
In der Sprache der Gruppentheorie, transformieren die Einheitsvektoren x und y als entartetes Paar.
124
Entartung
In C3v sind die Einheitsvektoren x und y gleichwertig. Besitzt ein Molekül mit C3v-Symmetrie eine Eigenschaft in der
x-Richtung, gibt es eine gleichwertige und von der ersten ununterscheidbare Eigenschaft in der y-Richtung.
Somit haben die Elemente eines entarteten Paars die gleichen Eigenschaften und unterscheiden sich nur in der
Ausrichtung.
Beispiel: Die px- und py-Orbitale sind in der C3v-Symmetrie ein entartetes Paar und haben somit die gleiche Form und
Energie (nicht aber die gleiche Ausrichtung).
125
Die !-Bindung in oktaedrischen Komplexen
(Bsp.: [Co(NH3)6]3+)
Die Ligandenorbitale werden in delokalisierte Orbitale kombiniert. Für einen oktaedrischen Komplex
erhält man aus den 6 Ligandenorbitalen 6 Linearkombinationen, die mit den "passenden" Metallorbitale
kombiniert werden. 1 LGO (') ist eine Linearkombination der 6 Atomorbitalen ("i):
" a1g =
1
(# x + # $ x + # y + # $y + # z + # $z )
6
?
M
6 Ligandenorbitale
$
6 LGOs
Die Linearkombinationen müssen Symmetrie-angepasst sein. Das heisst, ihr Symmetrieverhalten muss
mit der Oh-Punktgruppe kompatibel sein. Wir werden unten sehen (siehe "Reduktion"), wie solche
Linearkombinationen aufgebaut werden können.
Ein Metallorbital "passt" zu einem bestimmt LGO, wenn beide zur gleichen irreduziblen Darstellung
gehören.
126
Ligandengruppenorbitale (LGOs)
Die 6 Ligandeorbitale, die für die !-Bindung gebraucht werden, sind gegen das Metallatom gerichtet.
Die 6 p-Orbitale werden als Vektoren dargestellt:
M
Wie können wir die Form der LGO's bestimmen?
(
M
!"
Die aus der Kombination der 6 Einzelvektoren resultierenden LGOs sind eine Art "Supervektor", der 6
Komponenten besteht und mit der Oh-Symmetrie kompatibel ist.
Mit der Gruppentheorie kann man diesen "Supervektor" in seine Komponenten zerlegen. Wie oben
gesehen, erfolgt die Zerlegung (Reduktion) über das Symmetrieverhalten des Vektors, das durch die
Charaktere ausgedrückt wird. Die Charaktere der reduziblen Darstellung !" ermöglichen ihre Zerlegung
in die Komponenten.
Der erste Schritt ist somit die Bestimmung der Charaktere der reduziblen Darstellung !".
127
Reduzible Darstellung !"
Für !-Bindungen kann man eine vereinfachte Methode anwenden, um die Charaktere der !" zu bestimmen:
Charakter einer Symmetrioperation (SO) = Anzahl der Vektoren, die bei der SO in Ruhe bleiben
Oh
!"
E
6
8 C3 6 C2 6 C4 3 C2*
0
0
2
2
i
0
6 S4
0
8 S6
0
3 !h
4
6!d
2
* C 2 = C 42
Diese Faustregel funktioniert, weil Komponenten, welche unverändert bleiben, mit +1 multipliziert werden. Somit hat jede solche
Komponente Charakter = 1. Alle anderen Komponenten werden mit Null multipliziert. Diese Methode taugt nicht immer (siehe "Bindungen). Grund dafür ist, dass eine Komponente mit Koeffizienten )1 (z. B. –1) multipliziert werden kann.
128
Reduktion
N = 1 $ " rx #" ix #n x
hx
Die Reduktionsformel gibt an, wie oft (N-mal) eine bestimmte irreduzible Darstellung in der zu
reduzierenden Darstellung !" enthalten ist.
h = Gesamtzahl der Symmetrieoperationen in der PG
" rx = Charakter der Operation x in der reduziblen D.
!"
6
0 0
2
2
0
x
n = Anzahl von Operationen in der Klasse.
" ix = Charakter der Operation x in der irreduziblen D.
0 0 4
2
129
!" = a1g + eg + t1u
Die 6 LGOs bestehen aus
Metall-Orbitale:
1 LGO mit a1g-Symmetrie
2 LGOs mit eg-Symmetrie
3 LGOs mit t1u-Symmetrie
3d $ eg, t2g
4s $ a1g
4p $ t1u
130
M- und L-Orbitale der gleichen Symmetrie
Die Form der LGOs kann man aus der Gruppentheorie herleiten. Wir werden aber die LGOs graphisch
von der Form der passenden Metall-Orbitale ableiten:
Die Metall-t2g-Orbitale finden keinen passenden Partner in den LGOs! ($ keine Überlappung)
131
132
Energieniveaudiagramm (Oh)
Durch Überlappung der Orbitale gleicher Symmetrie an M und L6 entstehen die MOs des Komplexes.
133
Die t2g-Orbitale sind nichtbindend
134
Oktaedrische Komplexe: Kommentare zum Energiediagramm
Bsp.:
[Co(NH3)6]3+
$
$
Alle antibindende Molekülorbitale unbesetzt
$
Die nichtbindenden t2g-MOs vollständig besetzt
$
Alle bindende Molekülorbitale vollständig besetzt $
Die Bindungsenergie entspricht der Stabilisierung $
der 6 bindenden MOs.
$
Die "/"* -Aufspaltung ist kleiner für die d-Orbitale, weil ihre Überlappung mit den Liganden-eg-LGOs klein ist.
Die bindenden MOs sind hauptsächlich Liganden-Atomorbitalen, die antibindenden MOs werden eher durch Metall-AOs beschrieben.
Die nichtbindende MOs sind reine Metall-AOs.
*O entspricht der Energielücke zwischen nichtbindenden und antibindenden d-Orbitale. Starkes-Feld-Liganden bilden starke
Bindungen (= tiefe "-Energie, hohe "# -Energie). Die KFT betrachtet nur die Effekte auf nicht- und antibindende Orbitale!
Und [CoF6]3–?
135
Tetraedrische Komplexe
–
–
Metall-Orbitale:
Liganden-Orbitale
3d, 4s, 4p
2p
Metall-Orbitale:
3d $ e, t2
4s $ a1
4p $ t2
(9 Orbitale)
(4 Orbitale)
136
Erinnerung: Tetraedrische Komplexe in der KFT
137
Ligandengruppenorbitale (LGOs)
M
Reduzible Darstellung !"
Td
!"
E
4
8 C3
1
3 C2
0
6 S4
0
6 !d
2
(Charakter einer Symmetrioperation (SO) = Anzahl der Vektoren, die bei der SO in Ruhe bleiben)
Jetzt zerlegt man die reduzible Darstellung in irreduziblen Darstellungen.
138
Reduktion
N = 1 $ " rx #" ix #n x
hx
h
x
n
" rx
" ix
Gesamtzahl der Symmetrieoperationen in der PG = 24
Zahl der Operationen in der Klasse.
Charakter der Operation x in der reduziblen D.
Charakter der Operation x in der irreduziblen D.
!"
4
1
0
0
2
139
!" = a1 + t2
Die 4 LGOs bestehen aus
–
–
1 LGO mit a1-Symmetrie
3 LGOs mit t2-Symmetrie
s
M
M
dxy
pz
M
dxz
py
z
M
y
dyz
px
x
Die Metall-e-Orbitale finden keinen passenden Partner in den LGOs!
($ keine Überlappung, nichtbindend)
140
Energieniveaudiagramm (Td)
141
Tetraedrische Komplexe: Kommentare zum Energiediagramm
[CoCl4] 2–
Mischung von 3 Sätzen von
antibindend $
Orbitalen mit t2–Symmetrie
Daraus folgt, dass p- und
d-Metallorbitale vermischt
werden.
schwach antibindend $
Dies ist möglich, weil die
Td-Punktgruppe nicht zentrosymmetrisch ist, und die Unterscheidung zwischen g-und uOrbitale entfällt.
(spektroskopische Folgen:
siehe später)
bindend $
Wie in oktaedrischen Komplexen sind die bindenden MOs (t2, a1) hauptsächlich Liganden-Atomorbitalen, die antibindenden MOs (2
# t2* und a1*) werden eher durch Metall-AOs beschrieben. Die nichtbindende MOs (e) sind reine Metall-AOs.
*t entspricht der kleinsten Energielücke zwischen nichtbindenden und antibindenden d-Orbitale. Die t2-Metallorbitale (dxy, dxz, dyz und
p) sind nicht direkt zu den LGO's gerichtet. Deswegen ist die Überlappung zwischen den t2-Orbitalen gering. Demzufolge fällt die
Destabilisierung aller t2-Orbitale klein aus, und *t ist klein!
142
143
Die "-Bindung in oktaedrischen Komplexen
(Bsp.: [CoF6]3–)
Vorgehen:
???
2p
–
Analyse der Metall-Orbitale:
–
Analyse der Liganden-Orbitale
–
Kombination der Liganden-Orbitale Ligandengruppenorbitale, LGO
(2 # 6 Orbitale)
Erst die Reduktion der Darstellung der "-Bindung in [ML6] besagt, welche
Metallorbitale eine "-Bindung bilden können!
144
Reduzible Darstellung !$
M
Oh
!$
E
12
8 C3 6 C2 6 C4 3 C2*
0
0
0
–4
i
0
6 S4
0
8 S6
0
3 !h
0
6!d
0
* C2 = C42
Charakter einer Symmetrioperation (SO) = Anzahl der Vektoren, die bei der SO in Ruhe bleiben
Jetzt zerlegt man die reduzible Darstellung in irreduzible Darstellungen.
145
Reduktionsformel
N = 1 $ " rx #" ix #n x
hx
Die Reduktionsformel gibt an, wie oft (N-mal) eine bestimmte irreduzible Darstellung in der zu
reduzierenden Darstellung enthalten ist.
n x = Anzahl von Operationen in der Klasse.
h = Gesamtzahl der Symmetrieoperationen in der PG
" rx Charakter der Operation x in der reduziblen Darstellung.
!$
12
0
0
0
–4
0
"
0
x
i
= Charakter der Operation x in der irreduziblen Darstellung.
0
0
0
146
!$ = t1g + t2g + t1u + t2u
Die 12 LGOs bestehen aus
3 LGO mit t1g-Symmetrie
3 LGOs mit t2g-Symmetrie
3 LGOs mit t1u-Symmetrie
3 LGOs mit t2u-Symmetrie
Das Metall hat aber nur t2g- und t1u –Orbitale!
Die LGOs mit t1g- und t2u-Symmetrie finden keinen passenden Partner am Metall! ($ keine
Überlappung). Somit:
t1g
t2g
t1u
t2u
nichtbindend
bindend
bindend
nichtbindend
147
Die Form der "-Orbitale
Bindende "-Orbitale
z
y
y
x
x
t1u
t2g
M
M
t2u
t1g
Nichtbindende "-Orbitale
148
Energieniveaudiagramm (Oh)
149
"-Donoren
Bsp.:
"-Akzeptoren
[CoF6]3–
[Mo(CO)6]
150
Die spektrochemische Reihe
* nimmt in der Reihenfolge zu:
I– < Br– < S2– < SCN– < Cl– < N3– < F– < OH–, Harnstoff <
< O2–, Oxalat < H2O < NCS– < py, NH3 < en < bipy, phen <
< NO2– < P < H– + CH3–, C6H5– < CN– < CO
" -Donoren reduzieren *o:
I– < Br– < S2– < SCN– < Cl– < N3– < F– < OH–, Harnstoff <
< O2–, Oxalat < H2O < NCS– < NH3 < en
" -Akzeptoren erhöhen *o:
bipy, phen < NO2– < P < CN– < CO < NO+
151
"-Donoren und "-Akzeptoren
152
Wechselwirkungen zwischen Metall- und Ligandenorbitalen:
153
"-Donoren und "-Akzeptoren
3 Beispiele:
CO
(2 # d"-$*)
Die M$CO-Rückbindung betrifft die zwei senkrecht zu einander stehenden
"*-Orbitale des CO. Der CO-Ligand ist end-on gebunden.
C2H4 (d"-$*)
Die M$C2H4-Rückbindung benutzt das "*-C2H4-Orbital. Ethen ist ,2-koordiniert.
PX3
Die M$PX3 Rückbindung benutzt das !*-Orbital der P–X-Bindung (X = R, OR).
(d"-" *)
154
1. CO (2 # d"-$*)
CO (Reminder)
C
CO
O
(Huheey, S. 199)
Die 2 Elektronen im CO-HOMO sind das „lone pair“ auf C (Bild oben rechts). Diese bilden die dative !-Bindung
zum Metall.
155
Synergistische Bindung (= !-. /012):
die !-L$M-Donation un "-M$L-Rückbindung („back-donation“) verstärken sich gegenseitig:
156
Carbonylkomplexe [M(CO)6]
Die "-Bindung ist eine „"-Rückbindung“, weil sie Elektronendichte aus den gefüllten t2g-Metallorbitale in die unbesetzten "*-Orbitale
des CO-Moleküls transferiert:
Dadurch wird die Energie der t2g-Metallorbitale gesenkt:
157
Experimentelle Beweise für "-Bindungen
1. Infrarot-Spektroskopie
Die Wellenzahl %(CO) (genauer: die Kraftkonstante k) der C–O-Bindung ist ein Mass für die Stärke der
C–O-Bindung. %(CO) im freiem CO (g) beträgt 2143 cm–1.
Effekt der Elektronendichte am Metall:
d6-Komplexe
% (cm–1)
d10-Komplexe
% (cm–1)
[Mn(CO)6]+
2090
[Ni(CO)4]
2060
[Cr(CO)6]
[V(CO)6]
2000
–
1860
2–
1748
[Ti(CO)6]
–
1890
2–
1790
[Co(CO)4]
[Fe(CO)4]
Mit wenigen Ausnahmen ist %(CO) von Carbonylkomplexen immer niedriger als im freien CO. Deutung:
Die !-L$M-Bindung entfernt Elektronen aus einem schwach bindenden CO-Orbital (Bindungsordnung nimmt leicht
ab).
Die "-M$L-Bindung transferiert Elektronen zu einem stark antibindenden CO-Orbital (Bindungsordnung nimmt
stark ab).
Die C–O-Bindung wird durch die Koordination am Metall geschwächt (siehe später für Ausnahmen).
158
2. Strukturdaten (Elektronen- und Röntgenbeugung)
231 pm
CH3
OC
Re
CO
Kovalenzradius von sp3-hybridisiertem Kohlenstoff = 77 pm !
! somit ist der Kovalenzradiun von Re(I) = 154 pm
CO
OC
CO
200.4 pm
Kovalenzradius von sp-hybridisiertem Kohlenstoff = 70 pm !
! somit erwartet man 224 pm für die Re–C-Bindunglänge.
Die ist aber 24 pm kürzer ! "-Bindung!
Rankin, D. W. H.; Robertson, A. J. Organomet. Chem. 1976, 105, 331.
159
2. C2H4
(d"-$*)
160
C–C im Ethen: 134 pm
161
3. PR3 und P(OR)3 (d"-"*)
"-Bindung:
!*-(P–C)-Orbital
oder 3d-Orbital am P-Atom? $Hybrid von beiden!
162
"-Akzeptor-Eigenschaften
Die Elektronegativität der Substituenten am P-Atom bestimmt die "-Akzeptor-Eigenschaften (Wieso?):
PPh3: schwächer "-Akzeptor
P(OPh)3: stärker "-Akzeptor
163
Konkurrenz um die "-Elektronen
Cr–C trans zu CO = 188.0(4) pm
189.6(4) pm
164
Erklärung:
P(OPh3) ist ein stärkerer "-Akzeptor als PPh3!
165
Sterische Effekte von PR
3
und P(OR)3
„Cone Angle“:
Tolman, C: A. Chem. Rev. 1977, 77, 313.
166
Sterische Effekte auf die Reaktivität
Dissoziationsgleichgewichte und cone angle:
–L
0
[Pd (L)4]
–L
0
K1
[Pd (L)3]
K2
[Pd0 (L)2]
K1 und K2 nehmen in der Reihenfolge ab:
PPhtBu2 > P(Cyclohexyl)3 > P(iPr3)3 > PPh3 = PEt3 > PMePh2 > PMe3
Cone angle (°):
170
160
145
118
167
Weitere "-Akzeptor-Liganden
Ligandentyp
Bindungsart
Weitere Beispiele
CO
2 # d"-$*
N2, NO+
C2H2
1 # d"-$*
,2-O2
PR3
d"-" *
,2-H2, agostische Bindung
168
Vergleich N2 / CO
Im (symmetrischen) N2 sind die Lappen des "*-Orbitals gleichmässig auf den N-Atomen verteilt. Deshalb ist die
Überlappung zwischen den M- und N2-Orbitalen ist weniger effizient als mit CO:
N2
CO
Hinzu kommt, dass das N2-Orbital, das für die N2$M-!-Donation zuständig ist, energetisch tiefer liegt als im CO.
Somit ist N2 auch ein schwächer !-Donor als CO.
169
N2 als Ligand
N2 ist isoelektronisch mit CO, aber ein schwächer "-Akzeptor als CO. Deshalb, nur elektronenreiche
Komplexe binden N2, d. h. d6-Komplexe (gefüllte "-Orbitale) mit basischen Liganden (keine andere
starke "-Säuren (wie z. B. CO)!).
N2 ist auch ein schwächer !-Donor als CO, weil die Energie des lone pairs niedriger ist als im CO.
Molibdän(0):
170
Ruthenium(II):
IR:
[Ru(NH3)5(N2)]2+:
%(N2) = 1955 cm–1 (2331 cm–1 im freien N2)
171
NO+
NO+ ist isoelektronisch mit CO, aber ein noch stärker "-Akzeptor (+1-Ladung auf O)!
172
173
O2
(Zur Erinnerung)
Im O2-Molekül sind die "*-Orbitale z.T. besetzt.Um die Koordination zu ermöglichen, müssen die 2 ungepaarten e – in den
"*-Orbitale gepaart werden. Somit ist 1 der beiden Orbitale leer und kann die 2 e – der "- Rückbindung vom Metall
akzeptieren.
174
,2-O2
(,2 = „bishapto“ = 2 O-Atome binden zum Metall. Achtung: Es gibt auch ,1!)
d8
OC
PR3
Ir
O
O
Cl
PR3
"!2-O2"
Disauerstoff
Disauerstoff- oder Peroxokomplex?
d6
OC
In einer alternativen Beschreibung kann man den O2-Liganden als
Peroxo (O22–) betrachten.
PR3
Ir
O
Cl
PR3
Die Oxidationszahl des Metalls ist um 2 Einheiten höher als im ,2O2-Komplex.
O
"O22–"
Peroxo
Der Peroxo-Ligand ist ein 4-Elektronen-Donor und besetzt 2
Koordinationsstellen.
Die Gesamtelektronenzahl des Komplexes bleibt unverändert.
175
(,2-H2)
H
H
M
M
H
H
"klassisches"
Hydrid
"nichtklassisches"
Hydrid
Bindung:
!
"
H
H
!
besetzt
M
leer
!#
leer
M
H
H
besetzt
176
“Agostische“ C–H-Bindung
[W(CO)3(PCy3)2]
W–H(11a) = 2.27 Å
Kubas, G. J. J. Am. Chem. Soc. 1986, 108, 2294.
[Re(CO)3(PCy3)2]+
Re–H(11a) = 2.89(5) Å
Heinekey, D. M. J. Am. Chem. Soc. 1994, 116, 4515.
Die C–H-!-Bindung wirkt als 2-Elektronen-Donor und besetzt die 6. Koordinationsstelle.
Durch die !-Bindung und die "-Rückbindung wird die C–H-Bindung geschwächt.
177
Die "-Akzeptor-Reihe
178
Die "-Akzeptor-Reihe
NO+ > CO, RNC, PF3 > PCl3, C2H4, P(OPh)3 >
P(OEt)3 > C(OR)R > C2H2 > P(SR)3 >
PPh3 > PR3 > R2S > RCN >
Anilin > Alkylamine > Ether > Alkohole
179
!- und "-Effekte der Liganden: Ein Überblick
Die
Spektrochemische Reihe
bietet einen Überblick auf die kombinierten !- und "-Eigen-
schaften der Liganden:
I– < Br– < S2– < SCN– < Cl– < N3– < F– < OH–, Harnstoff < O2–,
Oxalat < H2O < NCS– < py, NH3 < en < bipy, phen < NO2– <
< PR3 < CH3–, C6H5– < P(OR)3 < CN– < H– < CO < NO+
(Quelle: Huheey, S. 473)
Starkfeld-Liganden sind entweder starke "-Akzeptoren (siehe oben) oder
starke !-Donoren (Hydrid, Alkyl) (siehe unten).
180
Was ist ein guter !-Donor?
Als gute !-Donoren werden Liganden bezeichnet, die eine koordinative !-Bindung mit starkem
kovalenten Anteil bilden. Dies bedeutet, dass die Orbitalüberlappung zwischen Metall und Liganden
gross ist (Beispiel: Hydrid, Phosphin).
Wie erkennt man, welche Liganden gute !-Donoren sind?
Durch die starke Überlappung mit dem Metallorbital schwächt ein starker !-Donor die Bindung zum
Liganden in der trans-Stellung (trans-Einfluss, siehe unten).
Wieso sind bestimmte Liganden bessere !-Donoren als andere?
Bedingung für die Bildung einer koordinativen Bindung mit starkem kovalenten Anteil ist, dass beide
Bindungspartner (Metall und Ligand) "weich" sind (harte und weiche Säuren und Basen, siehe unten).
181
trans-Einfluss
„The trans influence is defined as the extent to which a ligand weakens a bond trans to it in
the equilibrium state.“ (Pidcock A.; Richards, R. E.; Venanzi, L. M. J. Chem. Soc. (A), 1966, 1707.)
2.262(2) Å
2.30(2) Å
2.264(2) Å
Cl
Et3P
Pt
PEt3
PEt3
Et3P
Cl
Pt
Cl
2.29(9) Å
JPt,P = 2400 Hz
JPt,P = 3520 Hz
Cl
2.364(2) Å
2.374(2) Å
Ein Ligand, der eine koordinative Bindung mit grossem kovalentem Anteil bildet, will die transstehende M–L-Bindung schwächen (weil zueinander trans-stehende Liganden mindestens ein Metallorbital teilen müssen). Deshalb zeigt der trans-Einfluss, welche Liganden gute !-Donoren sind!
Der trans-Einfluss – und somit die kovalente "-Bindungsstärke – nimmt ab:
–
–
–
–
–
–
CH3 > H > PMe3 > CN > OH , Br > Cl > C2H4 > NH3 > py, F– > CO > OH2
Quelle: Sajith, P. K.; Suresh, C. H. Dalton Trans. 2010, 39, 815.
In der Folge werden wir ein Konzept besprechen, das diese Reihe erklärt (Weich/Hart-Konzept, siehe unten).
182
N. B.: Der trans-Einfluss ist ein thermodynamischer Effekt!
D. h., er wirkt im Grundzustand und wird aus Grundzustandseigenschaften des Komplexes gedeutet
(Bindungslängen, Kopplungskonstanten, IR-Schwingungsfrequenzen usw.
183
Spektrochemische Reihe und "- und $-Eigenschaften der Liganden
Stark-Feld-Liganden sind entweder starke "-Donoren (= Liganden, die "Bindungen mit starkem kovalentem Anteil bilden) oder starke $-Akzeptoren.
!-Donor-Reihe
Definitionsgemäss bilden starke !-Donoren starke !-Bindungen. Somit stabilisieren sie die !-bindenden
Orbitale und destabilisieren die !*-Orbitale. Resultat: *o, die Energiedifferenz zwischen t2g-Orbitalen
(mit n oder "-Charakter) und eg (!*-Orbitalen) nimmt zu.
Die kovalente "-Bindungsstärke nimmt ab (trans-Einfluss) (siehe oben) in der Reihe:
–
–
–
–
–
–
CH3 > H > PMe3 > CN > OH , Br > Cl > C2H4 > NH3 > py, F– > CO > OH2
Starke "-Donoren
Schwache "-Donoren
184
"-Akzeptor-Reihe
(Quelle: Huheey, S. 501)
Starke "-Akzeptoren stabilisieren die "*-Orbitale. Resultat: *o, die Energiedifferenz zwischen t2gOrbitalen (mit n oder "-Charakter) und eg (!*-Orbitalen) nimmt zu.
3 Starke $-Akzeptoren
NO+ > CO, RNC, PF3 > PCl3, C2H4, P(OPh)3 > P(OEt)3 > C2H2 > PPh3 >
R3 > R2S > RCN > Anilin > Alkylamine > Ether > Alkohole
Starke $-Donoren $
Spektrochemische Reihe
Resultiert aus der Überlappung beider Effekte:
3 Starke $-Akzeptoren oder !- Akzeptoren
NO+ > CO > H– > CN– > P(OR)3 > CH3–, C6H5– > PR3 > NO2– >
> bipy, phen > en > py, NH3 > NCS– > H2O > Oxalat, O2– > OH– >
> OH– > F– > N3– > Cl– > S2– > Br– > I–
Starke $- Donoren $
185
Harte und weiche Säuren und Basen
– HSAB-Prinzip als Faustregel
– Klassifizierung als „hart“ oder „weich“
– HSAB: Theoretische Grundlagen
– Elektronegativität & (Mulliken / Jaffé) und Absolute Härte '
– Matched (hard/hard, soft/soft) oder Mismatched (hard/soft)?
186
Die Koordinative Bindung als Lewis Säure-Base-Wechselwirkung $
$ HSAB-Prinzip (eine Faustregel)
Klasse a
Al(III), Ti(IV) und Co(III) bevorzugen N, O und F als Donoratome.
Harte Säuren verbinden sie sich bevorzugt mit harten Basen.
Klasse b
–
–
Ag+, Hg2+ und Pt2+ bilden stabilere Komplexe mit PR3, CN , I .
Weiche Säuren verbinden sie sich bevorzugt mit weichen Basen.
187
Klassifizierung als „hart“ oder „weich“
+
+
Konkurrenzreaktion zwischen der harten Säure H und der weichen Säure CH3Hg :
+
+
BH + CH3Hg
K
+
CH3HgB + H
Harte Base B:
3
Weiche Base B:
$
+
Beispiele:
CH3HgF + HSO3
weich-hart
–
hart-weich
CH3HgOH + HSO3
–
–
K + 103
CH3HgSO3 + HF
weich-weich
hart-hart
–
K > 107
CH3HgSO3 + H2O
Sowohl die Stärke als auch das HSAB-Verhalten müssen berücksichtigt werden.
Wenn die Stärken der Säure und der Base sehr unterschiedlich sind:
–
–
OH + CH3HgSO3 $ CH3HgOH + SO3
hart
weich-weich
weich-hart
2–
K = 10
weich
188
HSAB-Klassifizierung der Basen/Liganden
2 Reaktionen als Referenz:
HB(n–1)–
Kh
H+ + Bn–
CH3HgB(n–1)–
Kw
CH3Hg+ + Bn–
189
HSAB: Theoretische Grundlagen
Elektronegativität
(Huheey, S. 211 ff, 404 ff.)
& nach Mulliken / Jaffé
!=
Wieso? Beispiel: HCl (nach Pauling):
(Repetition)
I+A
2
H–Cl 4 H+ Cl– 4 H– Cl+
I
II
III
kovalent
Wenn Cl elektronegativer ist als H
ionisch
ionisch
$ der Beitrag der Struktur II ähnlich gross sein wie der von I.
Die Ionisierungsenergie I ist ein Mass für die Schwierigkeit, ein Elektron (oder, allgemeiner,
Elektronendichte) von einem Atom abzutrennen und ein Kation zu bilden.
Die Elektroneneaffinität A ist ein Mass für die Tendenz eines Atoms, negative Ladung aufzunehmen.
1
$2
! = 0.336 #% ( I
Zur Anpassung auf die Pauling-Skala:
&
(in eV) + A (in eV)) " 0.615 (
'
190
Ladung und Energie eines Atoms
Sowohl die erste Ionisierungsenergie als auch die (erste) Elektronenaffinität eines Atoms hängen näherungsweise
nach einer quadratischen Gleichung von seiner Ladung q ab (kann auch eine Teilladung sein!):
E = ( q + ) q2
Beispiel: F und Cl
191
Elektronegativität &
Jaffé hat gezeigt, dass die Definition der Elektronegativität & nach Mulliken gleich ist dem Anstieg (
dieser Energiekurve im Ursprung (q = 0). Beweis:
E = ( q + ) q2
Die erste Ableitung der Energie nach der Ladung q lautet:
dE
=(+2)q
dq
Somit gilt für q = 0:
! dE $
" dq &% q=0
&=#
=(
Beweis:
Für q = +1 $
Für q = –1 $
1) – 2) ergibt:
E = I = ( +)
E = –A = –( + )
I+A=2(
1)
2)
!=
$
I+A
=&
2
192
Härte '
Mit der Mulliken-Jaffé-Methode mann man die Elektronegativitäten partiell geladener Atome ermitteln. Ein Atom
mit einer negativen Partialladung übt eine geringere Anziehung auf zusätzliche Elektronen als ein neutrales Atom der
gleichen Sorte (= seien Elektronegativität ist geringer) (siehe E-q-Kurve). Um dies zu erkennen, kann man die
Elektronegativität & durch Expansion in Taylorreihe um q = 0 ausdrücken:
" d! %
! (q) = ! q=0 + q $
+ ...
# dq '& q=0
Somit entscheidet
Was ist aber
d!
, wie stark sich die Elektronegativität mit der Ladung q ändert.
dq
dE
d!
? Da & gleich
ist, folgt es:
dq
dq
d! d2E
=
dq dq 2
$
Krümmung der E-q-Kurve
Physikalische Bedeutung:
Kleine, "harte" (= kaum polarisierbare) Atome haben grosse Werte von
d2E
:
dq 2
Die Elektronegativität & nimmt schnell mit der Ladung ab, das Atom zieht zusätzliche Ladung nicht mehr an.
d2E
Grosse, "weiche" (= polarisierbare) Atome haben kleine Werte von
:
dq 2
Die Elektronegativität & nimmt langsam mit der Ladung ab, das Atom kann mehr Ladung anziehen (grössere
"Ladungskapazität").
193
Die Härte (') ist die Krümmung der E/q-Kurve!
E = ( q + ) q2
dE
=(+2)q
dq
d2E
dq 2
=2)
$ )=
1 d2E
2 dq 2
Beziehung zwischen Härte, I und A:
Zurück zur Beziehung zwischen E, I, und A:
Für q = +1 $
Für q = –1 $
1) + 2) ergibt:
E= I = ( +)
E = –A = –( + )
I–A=2)
$
!=
1)
2)
I–A
= " = absolute Härte
2
194
HSAB: Theoretische Grundlagen
Absolute Härte
!=
I"A
2
Absolute Elektronegativität
Absolute Härte von F2, Cl2, Br2 und I2:
!=
I+A
2
I = Ionisationspotenzial (eV);
A = Elektronenaffinität (eV)
Für „closed-shell“ Atome/Moleküle
(solche mit abgeschlossener Elektronenkonfiguration) gilt:
EHOMO = –I
ELUMO = –A
Somit ist die Härte gleich der Hälfte der
HOMO/LUMO-Lücke $
Das Ionisationspotenzial I ist massgebend für die Härte und für die Elektronegativität!
(Deshalb verlaufen ' und & etwa parallel zueinander.)
195
Absolute Härte (eV)
196
HSAB und Komplexe
harte Säuren / Basen
weiche Säuren / Basen
grosse HOMO/LUMO-Lücke
kleine HOMO/LUMO-Lücke
Ti
Ti–F
F
Ru
LUMO
LUMO
n
Bsp: d0-Komplex
HOMO
I
Ru–I
n
HOMO
Bsp: d6-Komplex
hart / hart
weich / weich
ionische Wechselwirkungen massgebend!
starke kovalente Bindungen (z.B. $-Bdg.)
hard / soft – mismatch:
instabil
(weder die ionische noch die kovalente Komponente der Bindung ist stark!)
197
198
Anwendungsbeispiele
1. trans-Einfluss
Wir haben oben gesehen, dass Phosphine einen grösseren tran-Einflus besitzen als Chloro:
2.262(2) Å
2.30(2) Å
2.264(2) Å
Cl
Et3P
Pt
PEt3
Et3P
Cl
JPt,P = 2400 Hz
Jetzt verstehen wir wieso:
PEt3
Pt
Cl
2.29(9) Å
Pt(II)
Cl–
PEt3
JPt,P = 3520 Hz
Cl
2.364(2) Å
2.374(2) Å
ist weich
ist hart
ist weich
Die Bindung zwischen einem weichen Metall-Ion wie Pt(II) und einem weichen Liganden wie Phosphin
ist stärker als die Bindung zwischen Pt(II) (weich) und Chloro (hart) (hard/soft mismatch).
Somit wird die Pt–Cl-Bindung in cis-[PtCl2(PEt3)2] durch die Pt–P-Bindung geschwächt. Dadurch
können die längeren Pt–Cl-Distanzen (und die kürzeren Pt–P-Dstanzen) im cis-Isomer erklärt werden.
199
2. Substitutionsreaktionen
Stabilitätskonstanten
als Indikatoren der Bindungsstärke
(Historisch: In wässriger Lösung)
–
[Fe(OH2)6]3+ + SCN (aq)
K1 =
[Fe(SCN)(OH2)5]2+ + H2O
[FeSCN 2+ ]
= 9 # 102
[Fe 3+ ][SCN ! ]
2+
[Cu(OH2)6]2+ + 4 NH3 (aq)
[Cu(NH3)4(OH2)2]2+ + 4 H2O
K4
3 )4 ]
= [Cu(NH
= 1 # 1013
2+
4
[Cu ][NH 3 ]
SCN bzw. NH3 binden das Metall-Ion stärker als H2O.
200
Systematische Trends
log K
[M(OH2)n]n+ + L (aq)
+
Ag
2+
Cu
K=
[ML(OH2)n–1]m+ + H2O
–
NH3
F
3.3
4.2
–0.2
0.9
–
–
Cl
Br
3.1
0.1
4.3
–0.1
Erklärung:
Ag(I) soft bindet F– (hart) eher schwach.
Cu(II) (borderline) hat schwache Affinität für Br– (weich).
[ML]
[M][L]
Elektronenspektren
–1-Elektron-Beschreibung und Terme
– Russel-Saunders-Kopplungsschema
(Beispiel: p2)
– Die Regeln von Hund
– Russell-Saunders-Terme
– Termenaufspaltung in schwachem oktaedrischem Feld
(Beispiel: d2)
– „Loch“-Formalismus
– Auswahlregeln für Elektronenübergänge, Extinktionskoeffizienten
– Tanabe-Sugano-Diagramme und Bestimmung von !o
– Der nephelauxetische Effekt
– Charge-Transfer-Spektren
– Tetragonale Abweichungen von der Oktaedersymmetrie und Jahn-Teller-Theorem
(Huheey, S. 504–534, 1139–1145 lesen!!)
202
Einleitung
Die bisher für Übergangsmetalle besprochene Energieniveaudiagramme beruhen auf dem sog.
1-Elektronen-Modell und sind – strikt betrachtet– nur für d1- und d9-Komplexe gültig.
Wenn das Metallion mehr als ein d-Elektron besitzt, " Elektron-Elektron-Abstossung.
Zwei Grenzfälle:
1
– die Kristallfeldaufspaltungen sind grösser als die Elektron-Elektron-Abstossung
(stark-Feld-Liganden, schwere Metalle).
– die Symmetrie des Komplexes ist niedrig.
Dann ist das 1-Elektronen-Modell zulässig.
2
– die Kristallfeldaufspaltungen sind klein (schwache Liganden, 3d-Metalle)
– die Symmetrie des Komplexes ist hoch.
Vorgehen: Grundzustand und angeregte Zustände des freien Ions (Terme) werden zuerst ermittelt.
Auf diese Zustände lässt man das Kristallfeld als Störung wirken.
203
Die 1-Elektron-Beschreibung
Dabei werden die Wechselwirkungen zwischen e – vernachlässigt!
204
Atomare Energiezustände / Terme
Wasserstoffatom:
Die Energie einer Spektrallinie und damit eines Elektronüberganges (zwischen stationären Zuständen)
ist durch die Rydberg-Gleichung gegeben:
#1
1&
# [cm–1] = 109737% " (
$ n12 n22 '
mit n2 > n1
Die Gleichung besteht aus zwei Termen:
Die Spektroskopiker charakerisieren mit dem Begriff Term die Energien der an dem Elektronenübergang beteilgten Zuständen.
(Huheey, Anhang C, S. 1139)
205
Atomare Energiezustände und Termsymbole
In einem Atom addieren sich die Bahn- (l) und Spinmomente (s) aller Elektrone.
Das Gesamtbahnmoment L ist angeben durch:
L = l1 + l2, l1 + l2 – 1, l1 + l2 – 2, ..., | l1 – l2 |
Die Komponente des Gesamtmomentes in Richtung einer gegebenen Achse ist:
ML = L, L – 1, L – 2, ..., 0, ..., –L
Die Zahl der möglichen Werte von ML beträgt 2 L + 1. ML ergibt sich auch als:
M L = ml1 + ml2 + ...+ ml n
Für die Spinquantenzahl gilt:
S = "s
i
Für einen gegebenen Wert von S gibt es 2 S + 1 Spinzustände, die durch Ms charakterisiert sind:
MS = S, S – 1, S – 2, ..., –S
oder
M S = ms1 + m s2 + ...+ ms n
206
Russel-Saunders-Kopplungsschema
Der Gesamtderhimpuls eines Elektrons ist die Vektorsumme aus dem Bahndrehimpuls und dem
Elektronenspin:
j=l+s
Wie bein einem Elektron treten auch in einem Atom Bahnmoment L und Spinmoment S in Wechselwirkung und
ergeben die neue Quantenzahl J:
J = L + S, L + S – 1, L + S – 2, ... |L – S|
Das Zustandekommen der J-Werte lässt sich aus der Darstellung der beteiligten Vektoren ersehen:
Russel-Saunders-Kopplungsschema nennt man auch LS-Kopplungsschema.
Alternative:
l + s " j (für jedes einzelne Elektron), j1 + j2 + ... + jn = J
(jj-Kopplungsschema)
207
Die p2-Konfiguration des Kohlenstoffatoms
1.
2.
3.
4.
Ermittlung der möglichen Werte für ML und MS.
Ermittlung der Elektronenkonfigurationen, die das Pauli-Prinzip erfüllen.
Tabellarische Erfassung der Mikrozustände.
Ableitung der Terme aus der Tabelle der Mikrozustände.
208
2
2
2
Termaufspaltung für den C-Grundzustand (1s 2s 2p )
209
Die Regeln von Hund
1. Grösstmögliche Spin-Multiplizität
Der Zustand mit dem grössten Wert für S besitzt die geringste Energie (" Grundterm).
(Weil der Term mit der grössten Spin-Multiplizität die grösste Austauschenergie besitzt.)
2. Grösstmöglicher L-Wert
Der Zustand mit dem grösseren Wert für L ist der energieärmere (bei gleicher Spin-Multiplizität).
3. J-Wert
Bei weniger als halb gefüllten Unterschalen ist der Term mit dem kleineren J-Wert der
energieärmere.
Bei mehr als halb gefüllten Unterschalen ist der Term mit dem grösseren J-Wert der
energieärmere.
210
Russell-Saunders-Terme
211
Vergleich zwischen Ein-Elektron-Näherung und LS-Kopplungsschema
212
Termen in einem SCHWACHEN oktaedrischen Feld
Bedeutung: Der energetische Abstand zwischen den Termen ist gross verglichen mit der Störung, die von den Liganden verursacht
wird.
Die Wellenfunktionen für die Terme S, P, D, F, G, usw. haben die gleiche Symmetrie wie die Wellenfunktionen der entsprechenden
Orbitale s, p, d, f, g, usw. " Der gleiche Aufspaltungsmuster entsteht!
213
d2-Ion
214
„Loch“-Formalismus
Ein Metallion mit d9-Konfiguration hat in seinem d-Niveau eine Elektronen-Leerstelle oder ein „Loch“
und kann daher sozusagen als ein inverses d1-Ion aufgefasst werden.
Diese beiden Konfigurationen, d1 und d9, haben daher den gleichen Grundzustandsterm 2D für das freie
Ion, und in einem Oktaederfeld entstehen in beiden Fällen die Niveaus 2T2g und 2Eg.
Die energetische Reihenfolge dieser beiden Niveaus ist jedoch bein einem d9-Ion gerade umgekehrt wie
die Anordnung für den d1-Fall.
Dieser Loch-Formalismus kann auch auf alle anderen dn-Konfigurationen angewandt werden: d2 und d8
bzw. d3 und d7 weisen identische Terme für den Grundzustand des freien Ions auf, aber die
Aufspaltungen im Oktaederfeld sind jeweils invers zueinander.
Eine ähnliche inverse Beziehung besteht auch zwischen den Aufspaltungsmustern in oktaedrischen und
tetraedrischen Ligandenfeldern. Hinzu kommt, dass die Symmetriebezeichnungen g und u bei den
tetraedrischen Komplexen entfallen, da diese kein Inversionszentrum aufweisen.
215
216
Auswahlregeln für Elektronenübergänge
1. Regel von Laporte
Nur solche Übergänge sind erlaubt, bei denen ein Wechsel der Parität stattfindet:
g "u
oder
u"g
Übergänge der Art g " g oder u " u sind verboten.
" Alle d-d-Übergänge in oktaedrischen Komplexen sind Laporte-verboten! (wenig intens)
" In tetraedrischen Komplexe gibt’s d-p-Mischung: die Laporte-Regel wird aufgehoben.
2. Alle Übergänge mit !S ! 0 sind verboten
Damit ein Übergang erlaubt ist, darf dabei keine Änderung der Spinmultiplizität stattfinden.
Die zweite Auswahlregel schränkt die Zahl der möglichen Übergänge drastisch ein.
In der d2-Konfiguration sind dann nur drei Übergänge spin-erlaubt:
3
T1g " 3T2g
3
T1g " 3A2g
3
T1g " 3T2g (P)
217
2
5
Spektren von d - und d -Komplexen
Oktaedrischer d2-Komplex: 3 Absorptionsbanden (unabhängig von Feldstärke).
Dies heisst aber nicht, dass alle Banden beobachtet werden können! (Hohe E " UV)
Oktaedrischer d5-Komplex: Der Grundzustand (6A1g) ist der einzige Zustand im Diagramm mit der
Spinmultiplizität 6. alle Übergänge sind sowohl Laporte- als auch spinverboten!
218
Extinktionskoeffizienten
219
Zahl der spin-erlaubten Übergänge
220
Tanabe-Sugano-Diagramme
berücksichtigen sowohl schwache als auch starke Felder (sind daher umfassender als OrgelDiagramme).
Sie ähneln den Korrelationsdiagrammen, sind aber zur Gewinnung quantitativer Aussagen wesentlich
nützlicher.
Der Grundzustand wird immer als Abszisse genommen, d. h. die Energien der angeregten Zuständen
werden relativ zum Grundzustand aufgetragen.
Die interelektronische Abstossung wird mit Hilfe der Racah-Parameter B und C ausgedrückt. B
und C sind Linearkombinationen von Coulomb und Austauschintegrale des freien Ions. Man erhält sie
als empirische Parameter aus den Spektren der freien Ionen.
B gibt die Energiedifferenz zwischen Zuständen gleicher Spinmultiplizität.
C braucht man für !E zwischen Zuständen verschiedener Multiplizität.
Parametrisierung durch B:
Energie E " E/B
Feldstärke " !/B
Vereinfachungen:
B $ 1 000 cm–1
C $ 4B
(für d6 C/B= 4.8)
221
Tanabe-Sugano-Diagramme
222
Racah-Parameter
223
6
Beispiel: d
High Spin:
Bei schwachem Oktaederfeld ist der Grundzustand 5T2g, (aus dem Term 5D des freien Ions).
[CoF6]3–-Spektrum:
5
T2g " 5Eg
ist der einzige Spin-erlaubte Übergang
Low Spin:
Unter den angeregten Zuständen auf der Seite des schwachen Feldes befindet sich ein Term 1A1g (aus
dem Term 1I des freien Ions), dessen Energie mit wachsendem ! steil abfällt.
Schliesslich wird 1A1g bei !/B = 20 der Grundzustand. An dieser Stelle tritt Spinpaarung ein, woraus die
Diskontinuität im Diagramm resultiert (senkrechte Linie).
[Co(oxalat)3]3–-Spektrum:
1
A1g " 1T1g
1
A1g " 1T2g
zwei Spin-erlaubte Übergänge
(weitere Übergänge bei höheren Energien werden durch vollständig erlaubte charge-transfer-Banden (siehe später) maskiert)
Da die Steigung des 1T2g-Terms viel grösser ist als die von 1T1g, nimmt der Abstand der beiden
Absorptionsbanden mit wachsender Feldstärke ! der Liganden zu.
224
[Co(en)3]3+
1
A1g " 1T1g
21 550 cm–1
1
A1g " 1T2g
29 600 cm–1
225
Bestimmung von !o
Durch Vergleich eines gemessenen Spektrum mit dem entsprechenden Tanabe-Sugano-Diagramm kann
man den Wert von ! für einen Komplex bestimmen (z.B.: [Co(en)3]3+). Vorgehen:
29600 cm"1
21500 cm"1
= 1.37
Aus dem Diagramm erkennt man, dass dieses Verhältnis bei !/B = 40 gegeben ist. Dort ist E/B = 37:
1
A1g ! 1T1g 21500
" B’ = 581 cm–1
=
= 37
B'
B'
! = 40 % B’ = 40 % 581 = 23 200 cm–1
B’ ist der Racah-Parameter B im Komplex.
Im freien Ion ist B = 1 100 cm–1 (siehe Tab. 11.18).
Somit:
581 cm !1 (im Komplex)
= 0.53
1100 cm !1B' (im freien Ion)
226
Die Koordination reduziert B (ein Mass für die Wechselwirkungen zwischen den Elektronen) um 47%!
(Nephelauxetischer Effekt, siehe unten).
227
Der Parameter B’
Der scheinbare Wert von B in Komplexen (als B’bezeichnet) ist immer kleiner als der des freien Ions (wegen der
Kovalenz):
228
Das Nephelauxetische Verhältnis
! = B’/B
!<1
Ist immer kleiner als 1 und sinkt mit zunehmender Delokalisierung (Kovalenz)
Die Nephelauxetische Reihe
B ! B'
= (1 ! " ) # h(Ligand) $ k(Metall)
B
nephelauxetischer Effekt/d-Elektronen-Delokalisierung (1–!) nimmt zu "
F– < H2O < dmf < OC(NH2)2 < NH3 < en < ox < NCS– < Cl– < CN– < Br– N3– < I–
Mn2+< V2+ < Ni2+ $ Co2+ < Mo2+ < Cr3+ < Fe3+ < Rh3+ $ Ir3+ < Co3+ < Mn4+ < Pt4+ < Pd4+
(B’ oder ! = B’/B nimmt ab ")
229
Ligand-to-Metal-Charge-Transfer-Spektren (LMCT)
Elektrontransfer von Orbitalen mit Ligandencharakter zu Orbitalen mit Metallcharakter.
[MnO4]–
L(t1) " M(e)
17 700 cm–1
L(t1) " M(t2*)
29 500 cm–1
L(t2) " M(e)
30 300 cm–1
L(t2) " M(t2*)
44 400 cm–1
Nur die Bande bei 17 700 cm–1 liegt im
sichtbarem Bereich (14 000 – 28 000 cm–1).
Sie verursacht die tiefviolette Farbe.
NB: Diese sind (u"g)-Übergänge und deshalb
Laporte-erlaubt. Wegen der grossen Extinktionskoeffizienten (102 bis 106 l mol–1 cm–1) verwendet man LMCT-Komplexe als Pigmente.
Ligand " Metall-charge-transfer-Übergänge (LMCT)
für einen tetraedrischen Komplex [ML4].
230
Metal-to-Ligand -Charge-Transfer-Spektren (MLCT)
Übergänge zwischen Orbitalen mit Metallcharakter und Orbitalen mit Ligandcharakter.
231
Abweichungen von der Oktaedersymmetrie
Elektronische oder strukturelle Faktoren können Abweichungen von der oktaedrischen Symmetrie verursachen. Da solche Abweichungen die Elektronenspektren stark beeinflussen können, werden sie in
diesem Kapitel diskutiert. Miteinbezogen werden auch Verzerrungen, die nicht unbedingt spektroskopisch relevant sind.
Tetragonale und Trigonale Verzerrungen des Oktaeders
Zuerst werden tetragonale Verzerrungen diskutiert, die durch die Art der Liganden verursacht werden.
Ein Beispiel sind pseudooktaedrische Komplexe der Zusammensetzung [MX2Y4].
232
Tetragonale Abweichungen: [CrF2(en)2]
+
Änderung der Energieniveaus eines d3-Ions
als Folge der Symmetrie-Erniedrigung von
oktaedrisch (Oh) nach tetragonal (D4h).
233
Effekt auf die d-Orbitalenergien
234
Bestimmte Elektronenkonfigurationen können Verzerrungen von der idealen Oktaedersymmetrie hervorrufen. Das Jahn-Teller-Theorem besagt, welche Moleküle dafür anfällig sind.
Das Jahn-Teller-Theorem
Bei nicht-linearen Molekülen, die sich in einem entarteten Zustand befinden, tritt eine Verzerrung auf,
die die Symmetrie erniedrigt, die Entartung aufhebt und die Energie senkt.
Keine Aussage über Grösse oder Art der Verzerrung (Stauchung oder Dehnung) (ausser dass das
Inversionszentrum erhalten bleibt.)
Die Aufspaltung der stark antibindenden eg-Orbitale ist wesentlich grösser als die der t2g-Orbitale, da
letztere entweder nichtbindend oder an schwachen &-Wechselwirkungen mit den Liganden beteiligt sind.
Aus den Tanabe-Sugano-Diagramme geht hervor, dass die einzigen Konfigurationen mit nicht-entarteten
Grundzuständen folgende sind:
high-spin d3 und d5, low-spin d6 und d8
Keine Jahn-Teller-Verzerrung erwartet!
235
Für alle anderen Konfigurationen erwartet man Jahn-Teller-Verzerrungen:
236
Beispiele:
d9, d4
Energieniveaudiagramm für die d9-Konfiguration im Feld von 6 oktaedrisch (Oh)
oder tetragonal-gedehnt (D4h) angeordneten Liganden:
237
238
Jahn-Teller-Verzerrungen und Reaktivität
Die Stabilisierung durch den Jahn-Teller-Effekt kann mit anderen strukturellen Effekten kollidieren.
Das typische Beispiel betrifft den Chelat-Effekt, der in der Folge besprochen wird.
239
Der Chelat Effekt
Chelatringe vergrössern die Stabilität von Komplexen erheblich. Diese Stabilisierung wird als ChelatEffekt bezeichnet.
Im Wesentlichen handelt es sich um einen Entropie-Einfluss, der allen Chelat-Systemen gemeinsam ist,
aber oft wird eine zusätzliche Stabilisierung durch eine negative Enthalpieänderung beobachtet.
Man betrachte die stufenweise Substitution zweier einzähnigen NH3-Liganden durch den zweizähnigen
Liganden Ethylendiamin (en) im Komplex [Ni(NH3)6]2+:
[Ni(NH3)6]2+ + en
[Ni(en)(NH3)4]2+ + en
[Ni(en)2(NH3)2]2+ + en
[Ni(en)(NH3)4]2+ + 2 NH3
[Ni(en)2(NH3)2]2+ + 2 NH3
[Ni(en)3]2+ + 2 NH3
K1
K2
K3
Da die Bindungsverhältnisse von Ammoniak und Ethylendiamin sehr ählich sind, erwartet man keine nennenswerte Enthalpieänderung für diese Reaktion. Aus den K1-, K2- und K3-Werten errechnet man folgende thermodynamische Daten:
240
(Hancock, R. D.; Martell, A. E. Comments Inorg. Chem. 1988, 6, 237.)
Der Ersatz von einzähnigen Liganden durch den Chelatliganden erhöht die Entropie in der Lösung:
!S = n R ln 55.5 = 33.4 n J K–1
Dabei ist n die Anzahl der Chelatringe. Bei T = 300 K ist der Entropie-Beitrag zur freien Enthalpie (pro Chelatring):
!G(Chelat) = –T!S = –(300 K) % (33.4 J K–1 mol–1) = 10.0 kJ mol–1
Dies stimmt mit den Daten in der Tabelle überein und zeigt, dass der Entropie-Beitrag zum Chelat-Effekt der grösste
ist.
241
Chelat-Effekt und Jahn-Teller-Verzerrung
Die Eigenart des Chelatringes in einem Komplex schränkt das Ausmass der möglichen Verzerrung des Oktaeders ein,
weil der Ligand durch den Abstand zwischen den koordinierenden Atomen eine bestimmte charakteristische
Spannweite, einen optimalen "Biss" (bite angle), besitzt:
H2
N
bite
angle
M
N
H2
Ein Beispiel für den Widerstreit zwischen der Stabilisierung durch den Jahn-Teller-Effekt und den geometrischen
Ansprüchen eines Chelat-Liganden findet man bei den Ethylendiamin-Komplexen von Cu(II). Die zweiwertigen
Ionen der meisten Übergansmetalle bilden Komplexe mit Ethylendiamin (en) durch stufenweisen Ersatz von Wasser:
[M(OH2)6]2+ + en
[Ni(en)(OH2)4]2+ + en
[Ni(en)2(OH2)2]2+ + en
[Ni(en)(OH2)4]2+ + 2 H2O
[Ni(en)2(OH2)2]2+ + 2 H2O
[Ni(en)3]2+ + 2 H2O
K1
K2
K3
Die Werte der Stabilitätskonstanten K1, K2 und K3 zeigen einen leichten Stabilitätsanstieg mit
wachsender Ordnungszahl von Mn(II) bis zum Ni(II):
242
Die Irving-Williams-Reihe
Stabilitätskonstanten von Ethylendiamin-Komplexen mit jeweils gleichen Liganden:
Mn2+ < Fe2+ < Co2+ < Ni2+ < Cu2+ > Zn2+
[Cu(en)3]2+ ist bemerkenswert unbeständig, obwohl er die grössten K1- und K2-Werte aufweist.
Erklärung: Für trans-[Cu(OH2)2(en)2]2+ ist eine Verzerrung dadurch möglich, dass sich die beiden trans-ständigen Aqua-Liganden
etwas vom Kupfer-Ion entfernen, während die beiden en-Ringe relativ unverändert bleiben. Der Energiegewinn durch diese JahnTeller-Verzerrung des d9 Cu(II)-Ions erklärt, wieso die mono- und bis-substituierten en-Komplexe besonders stabil sind. Im Gegensatz
dazu ist beim [Cu(en)3]2+ keine tetragonale Verzerrung möglich, ohne dass wenigstens zwei Chelatringe deformiert werden.
243
Kinetik und Chelat Effekt
Die Substitution eines chelierenden Ligandes is langsamer als die eines ähnlichen einzähnigen Ligandes.
Zwei Gründe:
– Der Chelat-Ligand is starker gebunden.
– Die Umkehrreaktion von (1) ist sehr wahrscheinlich.