Linearkombination von Vektoren

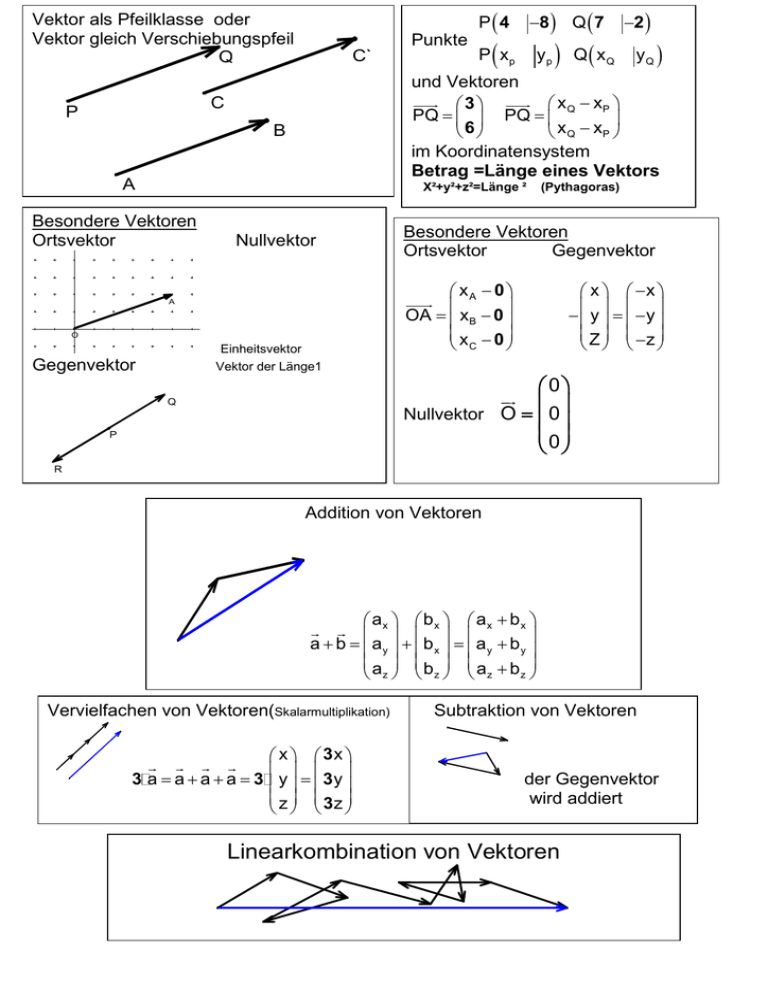
Vektor als Pfeilklasse oder
Vektor gleich Verschiebungspfeil
Q
Punkte
C`
8  Q  7

P xp
yp
B
A
X²+y²+z²=Länge ²
Besondere
Vektoren
y
Ortsvektor
Q
yQ 
(Pythagoras)
Besondere Vektoren
Ortsvektor
Gegenvektor
Nullvektor
 xA  0 
OA   xB  0 
 x 0
 C

A
x
O
Einheitsvektor
Gegenvektor
 Q x
2 
und Vektoren
 x Q  xP 
3
PQ    PQ  

6
 x Q  xP 
im Koordinatensystem
Betrag =Länge eines Vektors
C
P
P4
 x   x 
  y     y 
 Z   z 
   
Vektor der Länge1
 0
 
Nullvektor O  0
 
 0
 
Q
P
R
Addition von Vektoren
Q
Q
P
R
 Pa x   b x   a x  b x 
a  b   a y    b x    a y  b y 
a  b  a  b 
z
 z  z  z
R
Vervielfachen von Vektoren(Skalarmultiplikation)
 x   3x 
3 a  a  a  a  3  y    3 y 
 z   3z 
   
Subtraktion von Vektoren
Q
P
der Gegenvektor
wird addiert
R
Linearkombination von Vektoren
Verwendung von Linearkombinationen

Erzeugung von Punkten, die bestimmte Eigenschaften erfüllen z.B.
P so dass ABPC ein Parallelogramm wird.
M sei Mittelpunkt einer Strecke AB
Q teilt die Strecke AB im Verhältnis 2 zu 5


u.s.w.
Untersuchung von linearen Abhängigkeiten
Sind zwei Vektoren linear abhängig nennt man sind sie kollinear,
sind 3 Vektoren linear abhängig nennt man sie komplanar zueinander.
Vektorielle Geradengleichung und vektorielle Ebenengleichung
Eine Gerade ist durch zwei Punkte eindeutig bestimmt. Eine Ebene ist durch drei Punkte eindeutig bestimmt
x  a  k m
k R
x  OA  k  AB
k R
x  OA  k  AB  r  AC
k, r  R
𝒂∙𝒙+𝒃∙𝒚+𝒄∙𝒛−𝒅
𝒂∙𝒙+𝒃∙𝒚+𝒄∙𝒛=𝒅
√𝒂𝟐 +𝒃𝟐 +𝒄𝟐
=𝟎
Lagebeziehungen
Punkt und
Gerade

Gerade und
Gerade
Lösungsweg über die Berechnung von gemeinsamen Punkten:
Gleichsetzen der Vektorgleichungen
- P und g haben genau einen
gemeinsamen Punkt
- oder P und g haben keinen
gemeinsamen Punkt

- h und g haben genau einen gemeinsamen Punkt
- oder sie haben unendlich viele gemeinsame Punkte
- oder sie haben keinen gemeinsamen Punkte,
dann können sie windschief oder parallel
zueinander sein.
Ergänzungen zum Lösungsweg durch die Betrachtung der Vektoren
- h und g haben linear abhängige Richtungsvektoren ..(parallel)...........
- oder sie haben linear unabhängige Richtungsvektoren ...(nicht parallel).............
Zwei Vektoren des eindimensionalen Raumes sind grundsätzlich linear abhängig und kollinear.
Drei Vektoren des zweidimensionalen Raumes sind grundsätzlich linear abhängig und komplanar.
Sie können auch manchmal zufällig kollinear sein.
Vier Vektoren des dreidimensionalen Raumes sind grundsätzlich linear abhängig voneinander. Liegen
sie zufällig in einer Ebene, dann sind sie komplanar. Auch sie können manchmal kollinear zueinander
sein.
Skalarprodukt und Winkel zwischen zwei Vektoren. Skalarprodukt 0 wenn rechter Winkel
( )∙( )
𝑐𝑜𝑠𝜑 =
√ ∙√
Schnittwinkel von zwei Geraden , Winkel in einem Dreieck
Flächeninhalt eines beliebigen Dreiecks 𝐴 =
𝑎∙𝑏∙𝑠𝑖𝑛𝛾
2

vektorielle Ebenengleichung
Eine Ebene ist durch drei Punkte eindeutig bestimmt
x  OA  k  AB  r  AC
Normalengleichung
k, r  R
𝒂∙𝒙+𝒃∙𝒚+𝒄∙𝒛 =𝒅
HNF
𝒂∙𝒙+𝒃∙𝒚+𝒄∙𝒛−𝒅
√𝒂𝟐 +𝒃𝟐 +𝒄𝟐
=𝟎
Ergänzung Lagebeziehungen
Punkt und
Gerade

Gerade und
Gerade
Gerade und
Ebene
Ebene und
Ebene
Lösungsweg über die Berechnung von gemeinsamen Punkten:
Gleichsetzen der Vektorgleichungen
- P und E haben genau einen gemeinsamen Punkt
- oder sie haben keinen gemeinsamen Punkt

Punkt und
Ebene
- E und g haben genau einen
gemeinsamen Punkt
- oder sie haben keinen
gemeinsamen Punkt,
- oder sie haben unendlich viele
gemeinsame Punkte
-
E
E
1 und
2 haben unendlich viele gemeinsame
Punkte,
- oder sie haben keinen gemeinsamen Punkt,
- oder sie haben unendlich viele gemeinsame
Punkte, die auf einer Geraden liegen.
Ergänzungen zum Lösungsweg durch die Betrachtung der Vektoren
- h und g haben linear
abhängige
Richtungsvektoren
.............
- oder sie haben linear
unabhängige
Richtungsvektoren
........................
- die Spannvektoren von E und der Richtungsvektor von g sind linear abhängig
- die Spannvektoren von E und der Richtungsvektor von g sind linear unabhängig
- die Spannvektoren von
E1 und E2
sind paarweise
komplanar
- oder sie sind nicht paarweise komplanar
Zwei Vektoren des eindimensionalen Raumes sind grundsätzlich linear abhängig und kollinear.
Drei Vektoren des zweidimensionalen Raumes sind grundsätzlich linear abhängig und komplanar.
Sie können auch manchmal zufällig kollinear sein.
Vier Vektoren des dreidimensionalen Raumes sind grundsätzlich linear abhängig voneinander. Liegen
sie zufällig in einer Ebene, dann sind sie komplanar. Auch sie können manchmal kollinear zueinander
sein.
Abstandsberechnungen:
Punkt-Punkt
Punkt- Gerade
Gerade –Gerade
Punkt-Ebene
Gerade-Ebene
Ebene-Ebene
Skalarprodukt oder
kürzester Abstand oder
Kathete im
rechtwinkligen Dreieck
Lotgerade
oder HNF
spezielle hilfreiche Formeln
Kreuzprodukt  a   b   a b  a b 
2 3
3 2
1
1
a   b   a b  a b
 2  2  3 1 1 3
a  b  a b  a b
 3  3  1 2
2 1




Spatprodukt
windschiefe Geraden
Hilfsebene, in der
eine Gerade liegt
und die parallel zur
zweiten Gerade
liegt und dann
Abstand Gerade Ebene