Morphologische Klassifikation der Galaxien

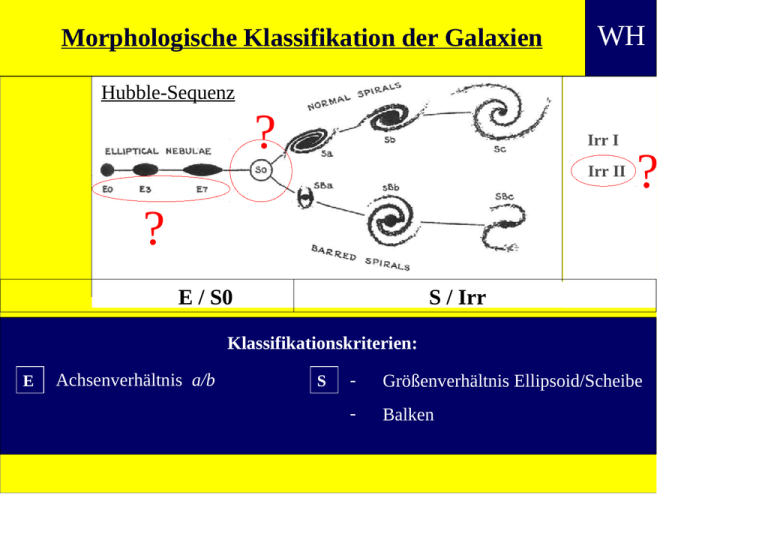
Morphologische Klassifikation der Galaxien
WH
Hubble-Sequenz
?
Irr I
Irr II
?
?
E / S0
S / Irr
Klassifikationskriterien:
E
Achsenverhältnis a/b
S
-
Größenverhältnis Ellipsoid/Scheibe
-
Balken
3. Eigenschaften normaler Galaxien
3.1 Helligkeitsprofile
3.2 Größe
3.3 Leuchtkraft
3.4 Spektrale Energieverteilung
3.5 Interstellares Medium
3.6 Verschiedene Spektralbereiche
3.7 Kinematik und Massen
3.8 Korrelationen
3.9 Entwicklungsmodelle
3.10 Spiralstruktur
Credits: NASA, ESA, Hubble Heritage Team
3.1 Helligkeitsprofile
Flächenhelligkeit 
I Strahlungsstrom pro Raumwinkeleinheit
 scheinbare Helligkeit pro Raumwinkeleinheit
(mag arcsec -2)
= 
2.5 log (I/I0)
0
Helligkeitsprofil:  (r )
Isophoten: Kurven mit const
(*) Definition analog zur scheinbaren Helligkeit m
*
3.1 Helligkeitsprofile
Bemerkung:
(1) Entfernung d
A1
1. Intensität:
I ∝ d -2
ω
2. Im Raumwinkel ω
erfasste Fläche A
am Ort der Quelle:
A ∝ d2
Beide Effekte kompensieren sich.
Flächenhelligkeit
ist unabhängig von
der Entfernung. *
(*) Für nicht zu große d,
wo kosmologische Effekte
vernachlässigbar sind.
(2) Entfernung 2d
A2 = 4 A 1
ω
3.1.1 Elliptische
M 87
r
Isophoten: konzentrische Ellipsen
3.1 Leuchtkraftprofile
3.1.1 Elliptische
(A) Allgemeines Profil:
Hubble-Profil
-2
I / I 0 = [r / a +1]
für r < 20 a
a: „Kernradius“
I0 : Zentrumsintensität
(a) empirisch
r
de Vaucouleurs-Profil
log I / Ie = -3.33[(r / re )¼ -1]
re : Radius, der ½ L enthält
d.h. log I ∝ -r 1/4 bzw. ∝ r 1/4
„r 1/4 - Profil“
Beide Beschreibungen liefern guten Fit an Beobachtung für r ~ a ... 20a.
3.1.1 Elliptische
3.1.3
Beispiele für Helligkeitsprofile
E1-Galaxie M 87
r 1/4
3.1.3
3.1.1 Elliptische
Beispiele für Helligkeitsprofile
μ
deVaucouleurs-Fit für
verschiedene E-Galaxien
eines Galaxienhaufens
(Virgo)
r 1/4
3.1 Leuchtkraftprofile
3.1.1 Elliptische
(A) Allgemeines Profil:
(b) Selbstgravitation
Helligkeitsprofil ist Ausdruck für die räumliche Dichteverteilung der Sterne
Aber: Warum sind Sterne so verteilt?
Elementare Prozesse:
1.
Stochastische Bewegung der Sterne
(„Sternengas“  „Gas“druck)
M
2.
Anziehungskraft durch gesamtes
Gravitationspotential aller Sterne
*
3.1 Leuchtkraftprofile
3.1.1 Elliptische
(A) Allgemeines Profil:
dA
(b) Selbstgravitation
r
P (r+dr)
dr
P (r)
Hydrostatisches GG einer Gaskugel:
Druckkraft dF P = Gravitationskraft dF G
dP
G Mr 
dA dr = 
2 dA dr
dr
r
dP
G Mr
=
dr
r2
r
mit Mr = ∫ 4r2dr
0
3.1 Leuchtkraftprofile
3.1.1 Elliptische
(A) Allgemeines Profil:
(b) Selbstgravitation
Ideales Gas (stoßfrei) aus Sternen der Masse M * :
P = kTn = kT/M
(k: Boltzmann-Konstante)
*
E in = 3/2 kT ( innere Energie)
E kin= 1/2 M *  2 (kinetische Energie der ungeordneten Bewegung)
:Geschwindigkeitsstreuung
Isotropie:
2
2
3
,:
r
r Streuung Radialgeschwindigkeit
Somit folgt für E in = E kin
P =   r2
3.1 Leuchtkraftprofile
3.1.1 Elliptische
(A) Allgemeines Profil:
(b) Selbstgravitation
Für Isothermie (d.h. const) ergibt sich dann
d
d ln4G 2
r2
=
r 
2
dr
d r  r
(
)
Näherungslösung:
King-Michie-Profil (*)
Lösung hängt nur von einem Parameter ab, dem
Konzentrationsparameter: c = log (rt / r0 ) mit
- r t Gezeitenradius (eine Art äußerer Radius)
- r 0 Kernradius (eine Art innerer Radius)
Interpretation der Lösung:
Aus(r)  M(r )  I (r)
(*) eingeschränkte Geschwindigkeitsverteilung
(v < Entweichgeschwindigkeit)
3.1 Leuchtkraftprofile
3.1.1 Elliptische
(A) Allgemeines Profil:
(b) Selbstgravitation
Vergleich der Dichte einer isothermen Kugel mit homogener Kugel in Projektion
Projizierte Dichte
King-Michie-Profil für r 0 / r t = 0.1
Homogene Kugel
0
0.2
0.4
0.6
0.8
1
Normierter Radius r / r t
Sehr starke Zentrumskonzentration!
3.1.1 Elliptische
3.1.3
Beispiele für Helligkeitsprofile
King-Michie-Fit für
ellipsoidale Objekte
verschiedener Typen
E-Galaxie
Galaxienhaufen
Kugelsternhaufen
3.1 Leuchtkraftprofile
3.1.1 Elliptische
(A) Allgemeines Profil:
(c) Ergebnis
Die beobachteten radialen Helligkeitsprofile von E-Galaxien
werden gut durch die (empirischen) Relationen von Hubble bzw.
de Vaucouleurs beschrieben.
●
●
Sie zeigen insbesondere eine starke Zentrumskonzentration.
Zugleich werden die gemessenen Profile durch das
King-Michie-Modell angepasst.
●
Schlussfolgerung: Die beobachteten Helligkeitsprofile
entsprechen denen von Gleichgewichtskonfigurationen der
Verteilung von Sternen (isotherme Sphäroide/Ellipsoide im
hydrostatischen GG), deren kinetische Energie durch die
ungeordnete Bewegung dominiert wird.
●
3.1.4
3.1.1 Ellipticals
(B) Feinstrukturen:
1. Abweichung von
Ellipsenform *
(a) disky E
zusätzliche Komponente
entlang großer Hauptachse
NGC 4697
(b) boxy E
Abweichungen zwischen
kleiner und großer Hauptachse
(*) Die Abweichungen sind nur
geringfügig und nur in den
Isophotenplots zu erkennen.
NGC 7785
3.8.2
3.1.1 Elliptische
(B) Feinstrukturen:
1. Abweichungen von Ellipsenform
θ
Messung der „boxyness“
Fourier-Entwicklung der Intensität I
entlang einer Ellipse:
a 4= 0
a 4>0
disky
a 4<0
boxy
I (θ) = I0 + a 1 cos(θ) + a 2cos (2θ) + a 3cos (3θ) + a 4cos (4θ) + ...
Abweichung von Elliptizität wird durch Fourier-Koeffizient a 4 gemessen:
= 0 reine E
> 0 disky, d.h. E mit Scheibenkomponente, ähnlich S0, aber schwächere Scheibe
< 0 boxy, d.h. kastenförmige Isophoten
Hubble-Sequenz: E und S0
E0/S0
E1
E3
S0 ähnlich wie disky E
(ellipsoid+disk)
disky E = Fortsetzung
der Hubble-Sequenz
links von S0 ?
E5
E6
E7/S0
Hubble-Sequenz
3.1.1 Elliptische
(B) Feinstrukturen: 1. Abweichungen von Ellipsenform
Naheliegende Modifikation
der Hubble-Sequenz:
reine E
disky E
Wie sind dann
aber die boxy E
einzuordnen?
3.1.5
3.1.1 Elliptische
(B) Feinstrukturen:
N
2. Verdrehung der Isophoten
•
Für ca. 50% ist a/b = const, P = const.
•
Für andere 50% Isophotendrehung
<ΔP> = 5° (...bis 60°)
<Δ(a/b)> = 0.04
P
ΔP
E
Mögliche Ursachen:
• Verformung durch nahe
Galaxien
• innere Struktur (triaxial?) +
Projektionseffekt (?)
3.1.6
3.1.1 Elliptische
(B) Feinstrukturen:
3. Ausgedehnte schwache Hüllen
•
Bogen-(Hüllen-)strukturen sehr
geringer Flächenhelligkeit
•
Für ca. 40% der E nachgewiesen
•
Oftmals viele Bögen bis zu sehr
großen Zentrumsabständen
Bild: NGC3923 (sehr stark kontrastverstärkt).
Insgesamt 26 Bögen (r bis ~200 kpc)
3.1.7
3.1.2 Spiralgalaxien
Unterschiede zu E-Galaxien:
(a) mehrere Komponenten
(b) mehr Strukturen

kompliziertere Profile
 „Profil-Dekomposition“, um
Scheibe und Bulge zu trennen
3.1.8
3.1.2 Spiralgalaxien
(A) Bulge
Im Prinzip ähnlich wie E,
aber auch Unterschiede:
1.
r1/4 - Gesetz gilt entlang
großer Achse, aber nicht
entlang kleiner Achse
2.
Bei gleichem L ist r B > r E
(Bulges sind weniger dicht)
3.
<a/b> B > <a/b> E
(Bulges sind flacher)
3.1.9
3.1.2 Spiralgalaxien
(B) Scheibe
Helligkeitsverlauf
unregelmäßig:
1.
Schwankungen um
Faktor ~2 wegen
Spiralstruktur
2.
darunter regulärer
Anteil
M 33
r
3.1.9
3.1.2 Spiralgalaxien
(B) Scheibe
Radiales Profil :
M 33
I ( r ) = I0 e- r/r s mit I 0 = const
d.h. μ ∞ r
(Freeman's law)
r s : Skalenlänge (~ 3... 5 kpc)
r
3.1.2 Spiralgalaxien
3.1.9
(B) Scheibe
Beispiele:
2
Ring mit
Gas-StaubWolken
log I
Bulge
1
Scheibe
0
M33
= NGC 598
0
10'
r
M 83
= NGC 5236
NGC 4459
20'
0
50''
r
100''
150'' 0
2'
r
4'
3.1.11
3.1.2 Spiralgalaxien
(B) Scheibe
NGC 4565
Vertikales Profil (*):
Aus Galaxien in (etwa) Seitenansicht:
•
für z groß : etwa wie e - (z/H)
•
für z klein : etwa wie e- (z/H)
2
entspricht Intensitäts-Profil der Form
I=I0 sech 2 (z / H),
H: Skalenhöhe
(*) nach Korrektur bzgl. Absorption
z
EXKURS
VertikalesStruktur
Profil einerMSS
selbstgravitierenden Scheibe
Hauptkomponenten der Kinematik der Sterne im MSS
- Kreisbahn um Galaktisches Zentrum (Rotation)
- Abweichung von Kreisbahn in R, θ und z
 Bewegungskomponente senkrecht zur Mittelebene z = 0
EXKURS
Ideale Bahn
Kreisbahn
mit z=0
Vertikales Profil einer selbstgravitierenden Scheibe
Galaktisches zyl. KS
Galaktische
Ebene
EXKURS
Vertikales Profil einer selbstgravitierenden Scheibe
Im Allgemeinen sind
die Bahnebenenzyl.
der Sterne
Galaktisches
KS aber geneigt.
Bahnebene
z ~ z max
t = t1
EXKURS
Vertikales Profil einer selbstgravitierenden Scheibe
Die Bahnneigung variiert
während des
Umlaufs
Galaktisches
zyl.
KS um das Gal. Zentrum.
Bahnebene
z~0
t = t2 > t1
EXKURS
Vertikales Profil einer selbstgravitierenden Scheibe
Die Bahnneigung variiert
während des
Umlaufs
Galaktisches
zyl.
KS um das Gal. Zentrum.
Bahnebene
z ~ z min
t = t3 > t2
EXKURS
Vertikales Profil einer selbstgravitierenden Scheibe
Galaktisches
 Pendelbewegung
um z = zyl.
0 beimKS
Umlauf um Zentrum
EXKURS
Vertikales Profil einer selbstgravitierenden Scheibe
Galaktisches zyl. KS
Epizyklische Näherung
Abweichung von Kreisbahn beschrieben durch Epizykel und Pendeln in z-Richtung
- Stern läuft auf Epizykel (entspricht ΔvR ,Δvθ)
- Epizykelzentrum läuft um galaktisches Zentrum auf Kreisbahn mit v K(R)
- Pendeln um z=0 entspricht Δv z
Epizykel
EXKURS
3.1.11
Vertikales Profil einer selbstgravitierenden Scheibe
Annahmen für theoretische Beschreibung:
- ausgedehnte axialsymmetrische Scheibe (Radius >> Dicke)
- dynamisches Gleichgewicht
- kinetische Energie durch Rotation dominiert
- planparallele, isotherme Schichtung
(isotherm heißt hier: Geschwindigkeitsstreuung σz unabhängig von z)
Aus „Jeans-Gleichungen“ = Kontinuitätsgleichung der Strömung in hydrodynamischer Näherung in Form der Momenten-Gleichung* (Herleitung im Seminar):
dρ
K
ρ: Gesamtmassendichte
= ρ z2
d z
σz
Kz: Kraftkomponente in z-Richtung
Poisson-Gl.:
d Kz
= -4πGρ
 d z
G: Gravitationskonstante
(*) erste und zweite Momente (Mittelwerte und Standardabweichungen) der Verteilung der
Geschwindigkeiten bzw. Beschleunigungen in Richtung R, θ, z.
EXKURS
3.1.11
ergibt
d
dz
Setzen:
Vertikales Profil einer selbstgravitierenden Scheibe
[
1 dρ
ρ dz
]
=
4πGρ
2
σz
D := ln ρ
ρ: Gesamtmassendichte
ergibt
dD
1 dρ
=
dz
ρ dz
Lösung:
1
2
ρ (z) = ρ0
z
z =ρsech
0
[exp(- H ) + exp( H )]2
mit
σz2
H := 
2πG
Skalenhöhe
( Hz )
3.1.2 Spiralgalaxien
3.1.11
(C) Dünne und dicke Scheibe
Manche Spiralgalaxien besitzen eine dünne und eine dicke Scheibe (auch MSS)
NGC 4565
R
z
R
Bulge dominiert Abweichung vom Modell bei großem R nicht durch Bulge
zu erklären ⇒ erfordert dicke Scheibe
3.1.10
3.1.2 Spiralgalaxien
(C) Dünne und dicke Scheibe
(a) gesamt
(b) Nach Subtraktion des Modells
einer dünnen Scheibe verbleibt
eine dicke Scheibe
3.1.7
Allgemeines Profil:
3.1.2 Spiralgalaxien
Ergebnisse
•
Bulges entsprechen, wie E-Galaxien, selbstgravitierenden Gleichgewichtskonfigurationen der Sternverteilung in Form isothermer Ellipsoide.
•
Scheiben entsprechen selbstgravitierenden Gleichgewichtskonfigurationen
der Verteilung von Sternen, deren kinetische Energie durch Rotation
domiiert wird, in Form einer ausgedehnten planparallelen Schichtung mit
der Skalenhöhe H und der Skalenlänge r s (H << r s ).
•
Spiralgalaxien können zwei (mehrere?) Scheibenkomponenten mit
unterschiedlichen Skalenhöhen H besitzen.
3.1.3 Helligkeitsprofile - Zusammenfassung
Elliptische Galaxien
●
empirisch: μ ~ r 1/4 (de Vaucouleurs)
entspricht selbstgravitierender Sternverteilung in Form von isothermen
Ellipsoiden im hydrostatischen GG wobei kinetische Energie durch
ungeordnete Bewegung dominiert wird
●
Unterscheidung:
reine E - disky E - boxy E
Spiralgalaxien
(a) Bulges:
ähnlich E, aber leichte Abweichungen
(b) Scheiben:
empirisch:
I ~ e -r / rs sech 2 (z / H)
(Freeman)
entspricht selbstgravitierender Sternverteilung in Form einer ausgedehnten
planparallelen, isothermen Schichtung (Skalenhöhe H, Skalenlänge r s )
wobei kinetische Energie durch Rotation dominiert wird