Von der Binomialverteilung zur Normalverteilung

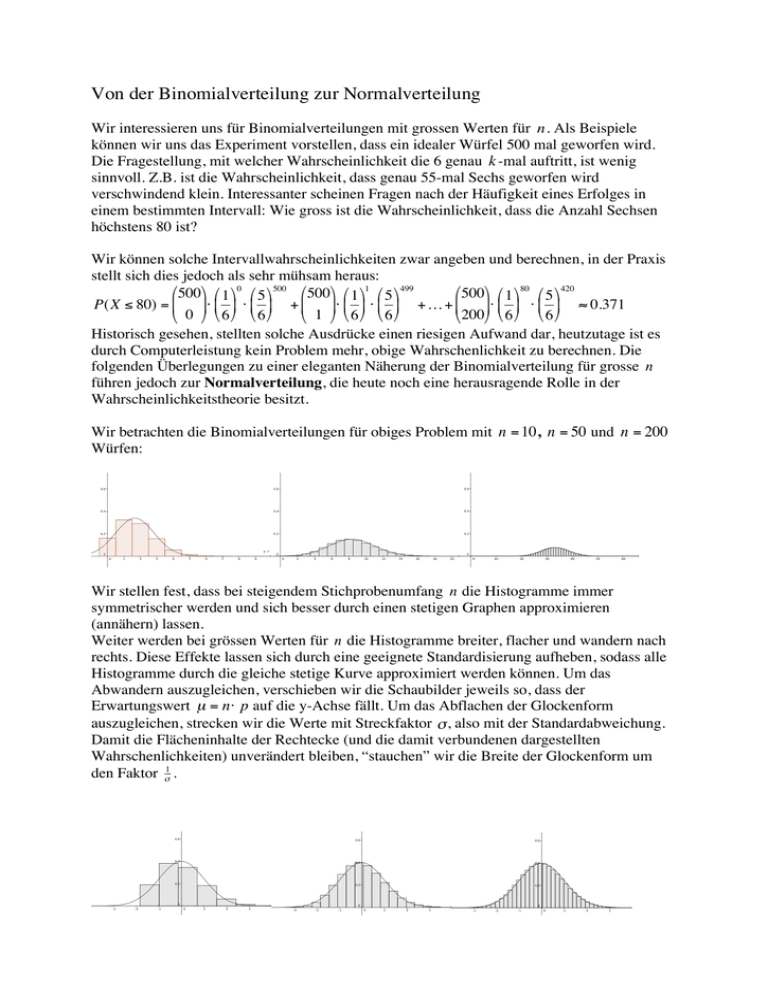
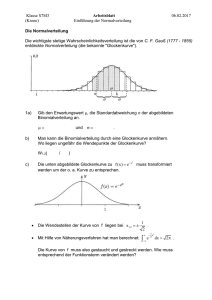
Von der Binomialverteilung zur Normalverteilung
Wir interessieren uns für Binomialverteilungen mit grossen Werten für n . Als Beispiele
können wir uns das Experiment vorstellen, dass ein idealer Würfel 500 mal geworfen wird.
Die Fragestellung, mit welcher Wahrscheinlichkeit die 6 genau k -mal auftritt, ist wenig
sinnvoll. Z.B. ist die Wahrscheinlichkeit, dass genau 55-mal Sechs geworfen wird
€
verschwindend klein. Interessanter scheinen Fragen nach der Häufigkeit eines Erfolges in
einem bestimmten Intervall: Wie gross ist die Wahrscheinlichkeit, dass die Anzahl Sechsen
€
höchstens 80 ist?
€
Wir können solche Intervallwahrscheinlichkeiten zwar angeben und berechnen, in der Praxis
stellt sich dies jedoch als sehr mühsam heraus:
# 500& # 1 & 0 # 5 & 500 # 500& # 1 &1 # 5 & 499
# 500& # 1 & 80 # 5 & 420
P(X ≤ 80) = %
(⋅ % ( ⋅ % ( + %
(⋅ % ( ⋅ % ( +… + %
(⋅ % ( ⋅ % ( ≈ 0.371
$ 0 ' $ 6' $ 6'
$ 1 ' $ 6' $ 6'
$ 200' $ 6 ' $ 6 '
Historisch gesehen, stellten solche Ausdrücke einen riesigen Aufwand dar, heutzutage ist es
durch Computerleistung kein Problem mehr, obige Wahrschenlichkeit zu berechnen. Die
folgenden Überlegungen zu einer eleganten Näherung der Binomialverteilung für grosse n
führen jedoch zur Normalverteilung, die heute noch eine herausragende Rolle in der
Wahrscheinlichkeitstheorie besitzt.
€
Wir betrachten die Binomialverteilungen für obiges Problem mit n = 10 , n = 50 und n = 200
Würfen:
€
€
€
Wir stellen fest, dass bei steigendem Stichprobenumfang n die Histogramme immer
symmetrischer werden und sich besser durch einen stetigen Graphen approximieren
(annähern) lassen.
Weiter werden bei grössen Werten für n die Histogramme breiter, flacher und wandern nach
€
rechts. Diese Effekte lassen sich durch eine geeignete Standardisierung aufheben, sodass alle
Histogramme durch die gleiche stetige Kurve approximiert werden können. Um das
Abwandern auszugleichen, verschieben wir die Schaubilder jeweils so, dass der
€
Erwartungswert µ = n⋅ p auf die y-Achse fällt. Um das Abflachen der Glockenform
auszugleichen, strecken wir die Werte mit Streckfaktor σ , also mit der Standardabweichung.
Damit die Flächeninhalte der Rechtecke (und die damit verbundenen dargestellten
Wahrschenlichkeiten) unverändert bleiben, “stauchen” wir die Breite der Glockenform um
€ 1.
den Faktor
σ
€
€
Es stellt sich die Frage, wie die Funktionsgleichung dieser stetigen “Glockenkurve” lauten
muss.
Logarithmiert man die dargestellten Wahrschenlichkeiten mit der ln -Funktion, so erhält man
ein Histogramm mit einer nach unten geöffneten Parabel:
€
Eine genaue Analyse liefert die die Gleichung dieser Parabel: y Parabel ≈ − 12 x 2 − 0.919 . Macht
man das Logarithmieren rückgängig durch Verwenden der Exponentialfunktion, so erhält
− 1 x 2 −0.919
−1 x2
−1 x2
man die Gleichung der ursprünglichen Funktion f (x) ≈ e 2
= e −0.919 ⋅ e 2 ≈ 12π ⋅ e 2
Die Funktion ϕ(x) =
1
2π
⋅e
− 12 x 2
€
heisst Gauss-Funktion.
€
Gehen wir zurück zur Einstiegsfrage: Wie gross ist die Wahrscheinlichkeit, dass die Anzahl
Sechsen bei 500-maligem Würfeln höchstens 180 ist? Die Wahrscheinlichkeit entspricht
€ einigem Verschieben, Strecken und Stauchen der Binomialverteilung) der markierten
(nach
Fläche unter der Treppenkurve, siehe Bild unten. Diese Wahrscheinlichkeit kann nun durch
das Integral der Gauss-Funktion approximiert werden:
a
P(X ≤ 80) ≈
∫ ϕ(t)dt ≈ 0.345
mit a =
−∞
€
80 − µ
(Verschieben um µ , stauchen um σ )
σ
Vergleicht man mit dem exakten Wert oben, liefert dies bereits für n = 500 eine gute
Näherung.
€
€
€
€
ϕ(t)
!
€
Eine Zufallsvariable mit der Wahrscheinlichkeit, dass die Zufallsvariable höchstens den Wert
x
x annimmt, P(X ≤ x) =
€
−∞
€
€
∫
1
2π
e
− 12 t 2
dt heisst normalverteilt. Die Funktion
−∞
x
Φ(x) =
∫
1
2π
e
− 12 t 2
dt heisst Gaussche Summenfunktion.
24.05.2013
Daniel Bürgy
Fachdidaktik 2 – Übung 5
Von der Binominalverteilung zur Normalverteilung
Wir betrachten im Folgenden die gleiche Aufgabe dreimal und entwickeln einen neuen
Lösungsweg. Der Lösungsweg der Aufgabe muss selbstverständlich jedes Mal
nachvollzogen werden.
Aufgabe: Es werden 600 Würfel geworfen. Mit welcher Wahrscheinlichkeit erscheinen
mindestens 95, höchstens 105 Sechser?
Lösung 1: P(95 ! x ! 105) =
" 600 % " 1 % x " 5 % 600*x
( $ x '& ) $# 6 '& $# 6 '& .
x=95 #
105
Bemerkung: Die Berechnung dieses Ausdruckes ist jedoch extrem aufwändig; man stelle
sich vor, der Ausdruck ist mit einem simplen Taschenrechner auszuwerten!
! n $ x
' p (1 ( p)n(x mit dem Erwartungswert
&
" x %
Die Binominalverteilung Pn (x) = #
µ = E(X) = np und der Standartabweichung ! = V (X) = np(1 ! p) lässt sich für grosse
Werte für n beliebig genau durch die sogenannte Gausssche Glockenkurve
1 # x" µ &
(
" '
" %
1
! µ," (x) =
! e 2$
" 2#
2
annähern. Dies geht aus dem zentralen Grenzwertsatz, einem der wichtigsten Ergebnisse
der höheren Wahrscheinlichkeitsrechnung, hervor.
Für das praktische Rechnen verwenden wir nun:
Pn (x) ! ! µ," (x) und
b+
b
!P
n
"
x=a
1
2
&#
µ ,$
(x)dx (!)
1
a%
2
Die Lösung der einleitenden Aufgabe würde nun wie folgt lauten:
1 ( x*100 )
* )
2 600) 1 ) 5
66
2
Lösung 2: P(95 ! x ! 105) =
" 600 % " 1 % " 5 %
)$ ' $ '
x '& # 6 & # 6 &
x=95
105
( $#
x
600*x
105.5
=
+
94.5
1
)e
1 5
600 ) ) ) 2!
6 6
dx
Bemerkung: Die Berechnung dieses Ausdruckes ist natürlich nicht einfacher als diejenige
von Lösung 1.
1
24.05.2013
Daniel Bürgy
Standardisierung (Normalverteilung)
Um die Berechnung tatsächlich zu vereinfachen, wird die Verteilung standardisiert.
Die Verteilung Pn (x) mit µ = np und ! =
np(1" p) wird um µ verschoben und in x-Richtung
1
und in y-Richtung um den Faktor ! gestutzt bzw. gestreckt. In der
!
1
$ x2
1
#e 2 .
Gausssche Glockenkurve wird nun µ = 0 und ! = 1 und damit ! 0,1 (x) = ! (x) =
2"
um den Faktor
Die entsprechenden Integralwerte liegen in Form von Tabellen vor (Formelbuch).
1 5
600 ! ! = 9.1287 . Die Integralgrenzen werden zu
6 6
1
-0.6025 und +0.6025 (Verschiebung µ um und Stutzung/Streckung um
/ ! ) und damit:
!
0.6025
0.6025
1
# &x 2
1
P(95 ! x ! 105) = $ " (x)dx = $
&e 2 dx = 0.4531
2%
#0.6025
#0.6025
Lösung 3: µ = 100, ! =
Das Verschieben und Stauchen/Stutzen kann anhand der folgenden Beispiels mit n=100 und
p=0.16 nachvollzogen werden.
Auf folgendem Link kann der Übergang von der Binominalverteilung zur Normalverteilung anschaulich, fast
praktisch nachvollzogen werden:
http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/binomialnormalverteilung/inhalt.html
2
Von der Binomialverteilung zur Normalverteilung
Übung5, Jonas Landolt, 24. 5. 2013
Wenn du einen Würfel 5 mal wirfst, wie gross ist dann die Wahrscheinlichkeit, dass du davon 3
oder 4 mal eine Sechs würfelst? Diese Wahrscheinlichkeiten können wir mit der Binomialverteilung ausrechnen. Wir bezeichnen mit k die Anzahl der Sechser.
!5 k
! !k
k 1
5
Wahrscheinlichkeit für k mal eine Sechs = P(X = k) =
·
5 6
6
Das können wir
natürlich
auch
in einem Balkendiagramm
darstellen:
Die Wahrscheinlichkeit, dass die Anzahl Sechser 3 oder 4 ist, ist somit:
! !4
! !3
!2
!
3 1
5
4 1
5
P(3  X  4) =
·
+
·
5 6
5 6
6
6
Wir stellen uns
nun vor, wir werfen den Würfel
100 mal. Die Binomialverteilung
schaut dann im
Balkendiagramm
so aus:
Wir möchten nun zum Beispiel die Wahrscheinlichkeit, dass wir zwischen 15 und 50 mal eine
Sechs würfeln, ausrechnen.
!
!15
!85
!
!50
!50
15
1
5
50
1
5
P(15  X  50) =
·
·
+ ... +
·
·
⇡ 0.7125
100
6
6
100
6
6
Dazu müssen aber 36 einzelne Wahrscheinlichkeiten ausgerechnet werden. Das wird uns auf die
Dauer zu mühsam. Des weiteren wollten wir auch ähnliche Aufgaben lösen können, wenn der
1
Würfel 1’000 mal oder noch mehr geworfen wird.
Die Wahrscheinlichkeit P(15  X  50) entspricht der Fläche der Balken von 15 bis 50 im Bild.
Da wäre es doch sinnvoll mit einer Kurve die Fläche etwa zu beschreiben und dann einfach den
Bereich vom Balken bei 15 bis zum Balken bei 50 zu integrieren.
Dazu müssen wir eine Kurve finden, die ähnlich aussieht wie das Balkendiagramm. Was meinst
du dazu?
x2
Das ist die Kurve f (x) = p1 e 2
e ⇡ 2.718
2⇡
und wir nennen sie Standardnormalverteilung. Sie passt
jedoch noch nicht schön auf das Balkendiagramm. Dazu
müssen wir sie noch ein wenig zurecht "drücken".
Um sie schön über die Balken zu schieben ersetzen wir x durch x µ und korrigieren die Konstante am Anfang indem wie sie durch teilen. Dabei ist µ der Erwartungswert und 2 die Varianz.
Die Funktion f (x) =
2.
p1
2⇡
e
2
(x µ)2
2
nennt man die Normalverteilung mit dem Erwartungswert µ
und der Varianz
Als Repetition: Bei der Binomialverteilung gilt µ = np und
In unserem Fall heisst das somit: µ = 100 · 16 ⇡ 16.7 und
Und unsere verschobene Funktion ist f (x) =
p1
2⇡
2
e
(x µ)2
2
⇡
2
2
= np(1 p).
= 100 · 16 · 65 ⇡ 13.9.
p 1
e
27.8·⇡
(x 16.7)2
27.8
Diese Funktion passt nun ziemlich schön auf das Balkendiagramm. Tatsächlich kann man beweisen, dass je
grösser die Anzahl Versuche bei der Binomialverteilung
ist, desto genauer wird diese durch die Normalverteilung
approximiert.
Um nun P(15  X  50) zu berechnen integrieren wir
einfach diese Funktion von 14.5 bis 50.5. Der Balken für
k = 15 beginnt nämlich schon bei 14.5 und der Balken
für k = 50 endet erst bei 50.5. Tatsächlich liefert dies den
Wert 0.7191. Eine ziemlich gute Approximation.
Wenn der Würfel nur wenige mal geworfen wird, ist diese Approximation zu ungenau. Doch um
Binomialverteilungen mit ”Anzahl Versuche” = n > 4p2 (11 p)2 zu approximieren, lieferte dieser
Weg brauchbare Werte.
2
Mathematik Fachdidaktik II, Übung 5 #
#
#
24. Mai 2013
Theorie: Die Normalverteilung
Wir betrachten drei Histogramme mit Stichproben derselben Grundmenge. Die
Grundwahrscheinlichkeit beträgt im Beispiel p=½, aber die Stichprobengrösse sind verschieden
(n=4, 8 resp. 12).
Beobachten Sie, wie die höchste Säule nach rechts
rückt und die Anzahl Säulen wächst. Das Histogramm wird dadurch breiter und flacher.
Um die Histogramme besser vergleichen zu können, werden wir sie nun standardisieren.
1. Schritt Verschieben des Mittelwerts E(Χ) auf die y-Achse.
Dadurch wird das ,,Wandern'' des Mittelwertes verhindert.
Hierfür definiert man eine neue Zufallsvariable: Y= Χ-E(Χ).
2. Schritt Normieren der Standardabweichung auf 1.
Dadurch wird die Ausbreitung des Histogramms verhindert.
Hierfür definiert man eine neue, die standardisierte Zufallsvariable:
Y χ − E( χ )
Z= =
σ
σ
Dies hat auch zur Folge, dass die Säulenbreite nun statt 1 neu 1/ σ ist.
#
Wir können jetzt beweisen, dass wir mit unseren Überlegungen und Herleitungen tatsächlich
das gewünschte Resultat erreicht haben, also
1
µ
1
µ
1
µ
E(Z ) = E( χ − ) = E( χ ) − E( ) = µ − = 0
1
σ
σ
σ
σ
σ
σ
µ⎞ 1
µ
⎛1
Var(Z ) = Var ⎜ χ − ⎟ = 2 Var( χ ) − Var( ) = 1
⎝σ
σ⎠ σ
σ
3. Schritt Säulenhöhe justieren
Damit weiterhin die Säulenfläche der Wahrscheinlichkeit des jeweiligen Ereignisses
entspricht, muss die Säulenhöhe mit σ multipliziert werden.
Jetzt können Sie die oberen Histogramme mit ihren standardisierten Formen unten vergleichen.
µ
µ
E( ) =
σ
σ
1 Da der Erwartungswert einer Konstanten die Konstante ist, gilt
Mathematik Fachdidaktik II, Übung 5 #
#
#
24. Mai 2013
Mit wachsendem n nähert sich das Histogramm der eingezeichneten „Glockenkurve” an.
Wir vermuten, dass sich die Treppenfunktion bei n → ∞ einer glatten „Glockenkurve” annähern
wird.
Jede binomialverteilte Zufallsgrösse Χ kann auf diese Weise standardisiert werden. Das
Histogramm der zugehörigen standardisierten Zufallsgrösse Z kann in jedem Fall durch ein- und
dieselbe Glockenfunktion angenähert werden. Diese Glockenfunktion wird auch Gaußsche
Glockenfunktion oder Normalverteilung genannt. Ihre Funktionsgleichung2 lautet:
−t
1
φ (t) =
⋅e 2
2π
2
Ist die Laplace -Bedingung:
n ⋅ p ⋅(1− p) > 9
erfüllt, ist die Normalverteilung eine gute Näherung für die Binomialverteilung.
In diesem Fall kann man die Normalverteilung benutzen, um Wahrscheinlichkeiten für
binomialverteilte Zufallsgrössen zu berechnen. So werden die Rechtecksflächen des Histogramms
in Integrale bei der Normalverteilung übergehen.
Literatur:
Lambacher-Schweizer Mathematik: Stochastik Grundkurs; Ernst Klett Verlag; Stuttgart, 1986
Cornelsen: Stochastik Kursstufe; Berlin, 1995
Mathematik für Schule und Praxis: Wahrscheinlichkeitsrechnung und Statistik, Band 1; H.C.
Reichel (Hrsg.); Wien 1987
DMK: Formeln, Tabellen, Begriffe. Mathematik - Physik - Chemie;
Mathematik heute: Leistungskurs Stochastik; Schroedel Schulbuch Verlag; Hamburg 1984
2
Die Funktionsgleichung der Gaußschen Glocke kann im Unterricht leider nicht hergeleitet werden.
Didaktische Übung 5: Theorieblatt: „Von der
Binomialverteilung zur Normalverteilung“
22. Mai 2013
Sacha Wolf
1
Motivation zur Theorie
Betrachtet man verschiedene Histogramme der Binomialverteilung, so fällt auf, dass sie immer glockenförmig sind. Ein solches Histogramm für B20,0.5 (k) ist in der folgenden Abbildung gezeichnet. Wir wollen
nun in ein Histogramm der Binomialverteilung eine Funktion derart legen, dass die Binomialverteilung
gut approximiert wird.
P (X = k)
0.4
0.2
−1 0
2
1
2
3
4
5
6
7
8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 k
Von der Gaussglocke zur Dichtefunktion
0.4
Die links abgebildete Kurve nennt man
Gaussglocke, nach dem Mathematiker Carl
Friedrich Gauss, der sich intensiv mit dieser
Funktion befasst hat. Ihre Funktionsgleichung
lautet
1 1 2
ϕ(x) = √ e 2 x .
2π
ϕ
0.2
−3
−2
−1
0
1
2
Im Folgenden wollen wir nun zeigen, dass diese
Gaussglocke – wenn man sie etwas verändert
– die Kurve der Binomialverteilung gut approximiert. Das zeigen wir in drei Schritten.
3 k
1
2.1
Erster Schritt: Verschiebung
Die Binomialverteilung hat ihr Maximum
beim Erwartungswert µ. Dementsprechend
verschieben wir die Gaussglocke um µ nach
rechts, das ist in der nebenstehenden Abbildung gezeigt. Algebraisch entspricht dies dem
Übergang zur neuen Funktionsgleichung
2
1 1
ϕ(x − µ) = √ e 2 (x−µ) .
2π
2.2
0.4
0.2
−10 −5
15
20
25
30
35
5
10
15
20
25
30
35
5
10
15
20
25
30
35
0.4
0.2
2
1
1
1
ϕ(x − µ) = √ e 2 (x−µ) .
σ
σ 2π
−10 −5
Dritter Schritt : Streckung
Zuletzt wird die Funktion in x-Richtung um
den Faktor σ gestreckt. Somit erhalten wir die
neue Funktionsgleichung
!
"
1 x−µ 2
1
1
x−µ
ϕ
= √ e2( σ ) .
σ
σ
σ 2π
Wir nennen diese Funktion Dichtefunktion.
3
10
Zweiter Schritt: Stauchung
Als nächstes stauchen wir die Gausskurve um
den Faktor σ1 entlang der y-Richtung. Auf diese Weise erhalten wir die neue Funktionsgleichung
2.3
5
0.4
0.2
−10 −5
Die Normalverteilung
Bei der Binomialverteilung geschieht die Berechnung der Wahrscheinlichkeit P (a ≤ X ≤ b) derart, dass
wir im Histogramm die Flächen sämtlicher Balken zwischen a und b summieren.
Wenn Sie sich daran erinnern, dass mit Hilfe eines Integral die Fläche unter einer Kurve berechnet wird,
können wir nach der neu eingeführten Theorie entsprechend P (a ≤ X ≤ b) als Fläche betrachten, die sich
durch Integration der Dichtefunktion zwischen a und b ergibt:
# b
1 x−µ 2
1
√ e 2 ( σ ) dx.
P (a ≤ X ≤ b) =
a σ 2π
Dieses Integral zu berechnen ist aber sehr schwierig, da es sich nicht auf eine elementare Stammfunktion
zurückführen lässt. Man schreibt deshalb
"
!
"
!
# b
1 x−µ 2
1
a−µ
b−µ
(
)
2
σ
√
e
−Φ
P (a ≤ X ≤ b) =
dx = Φ
σ
σ
a σ 2π
$
%
&
'
und schlägt die Werte Φ b−µ
in einer Formelsammlung nach oder berechnet sie mit dem
und Φ a−µ
σ
σ
Computer bzw. Taschenrechner. Wir wollen festhalten: Eine Zufallsgrösse X heisst normalverteilt mit
Erwartungswert µ und Standardabweichung σ, wenn sich die Wahrscheinlichkeit P (a ≤ X ≤ b) berechnen
lässt als Integral
"
!
"
!
# b
1 x−µ 2
1
a−µ
b−µ
(
)
2
σ
√ e
P (a ≤ X ≤ b) =
−Φ
.
dx = Φ
σ
σ
a σ 2π
2