Ach die Ähnlichkeit

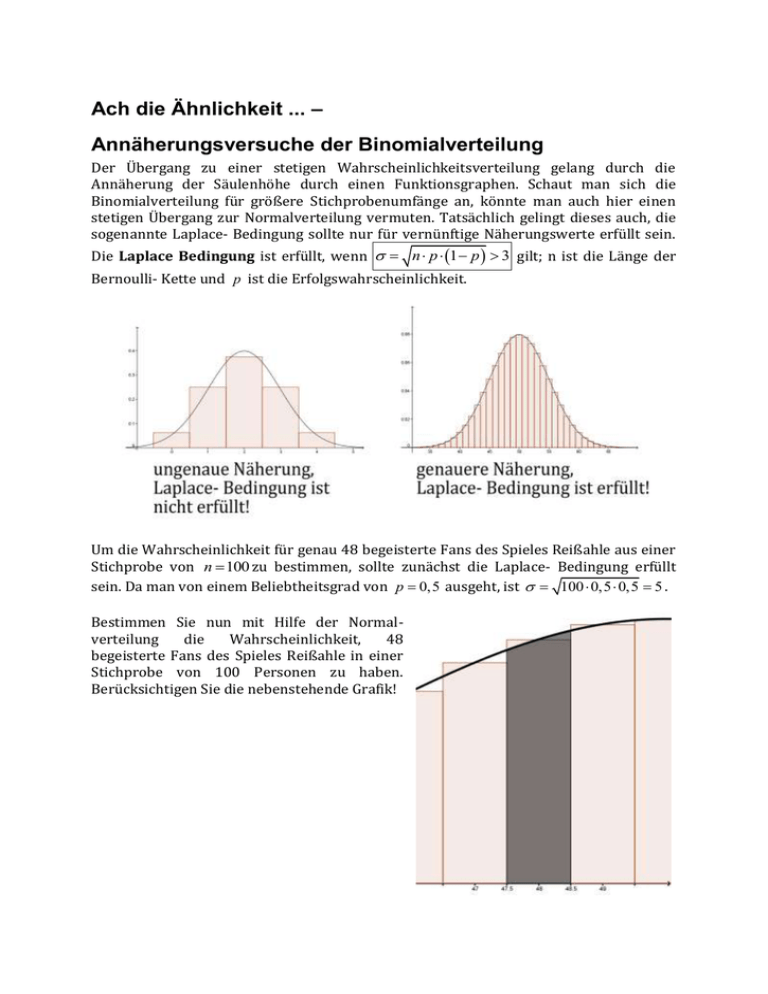
Ach die Ähnlichkeit ... –
Annäherungsversuche der Binomialverteilung
Der Übergang zu einer stetigen Wahrscheinlichkeitsverteilung gelang durch die
Annäherung der Säulenhöhe durch einen Funktionsgraphen. Schaut man sich die
Binomialverteilung für größere Stichprobenumfänge an, könnte man auch hier einen
stetigen Übergang zur Normalverteilung vermuten. Tatsächlich gelingt dieses auch, die
sogenannte Laplace- Bedingung sollte nur für vernünftige Näherungswerte erfüllt sein.
Die Laplace Bedingung ist erfüllt, wenn   n  p  1  p   3 gilt; n ist die Länge der
Bernoulli- Kette und p ist die Erfolgswahrscheinlichkeit.
Um die Wahrscheinlichkeit für genau 48 begeisterte Fans des Spieles Reißahle aus einer
Stichprobe von n  100 zu bestimmen, sollte zunächst die Laplace- Bedingung erfüllt
sein. Da man von einem Beliebtheitsgrad von p  0,5 ausgeht, ist   100  0,5  0,5  5 .
Bestimmen Sie nun mit Hilfe der Normalverteilung
die
Wahrscheinlichkeit,
48
begeisterte Fans des Spieles Reißahle in einer
Stichprobe von 100 Personen zu haben.
Berücksichtigen Sie die nebenstehende Grafik!
Für die Wahrscheinlichkeit, dass man 48 begeisterte Fans vorfindet, muss die
Säulenfläche bei k  48 berechnet werden. Überträgt man diese Überlegungen auf die
Normalverteilung, würde ohne Korrektur das Ergebnis für k  48 durch

48
 x   2
2 2
1
e
dx  0

48  2
gegeben sein. Nur in dem man links als auch rechts eine Korrektur von 0,5 vornimmt,
macht das Ergebnis Sinn:
48,5
1
47,5  2  e

 x   2
2
48,5
2
dx 
1
47,5 5 2  e

 x 50 2
50
dx  0, 0736 .
Zum Vergleich mit der binomialverteilten Zufallsvariable X :
P  X  48  B100;0,5  48  0,0735
Berechnen Sie Mit Hilfe der Normalverteilung die Wahrscheinlichkeit, dass nun
mindestens 47 und höchstens 49 begeisterte Fans in der Stichprobe ( n  100 ) zu finden
sind. Zur Hilfestellung nehmen Sie das Schaubild auf der vorherigen Seite! Vergleichen
Sie Ihr Ergebnis mit der entsprechenden binomialverteilten Wahrscheinlichkeit.