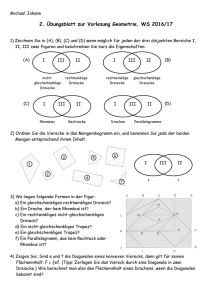
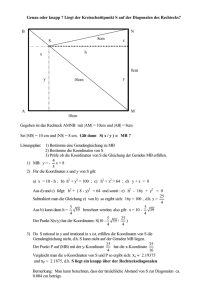
Diagonalen, diedenRahmensprengen

Mathe-Olympiade Hessen 2010 // TU Darmstadt
n
e
g
n
e
,
pr
n
s
e
l
n
e
na
m
o
h
g
a
a
Di
nR
e
d
die
Mathe-Olympiade Hessen
27. Februar 2010
Martin Otto
Arbeitsgruppe Logik
Fachbereich Mathematik
Technische Universität Darmstadt
www.mathematik.tu-darmstadt.de/˜otto
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
1/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
11
1 1
1 1 1 1
11
11
11
11
11
11
1 1 1
paradox?
1
11
11
11
11
11
11
11
11
11
11
11 1
111
11
11
11
11
11
11
11
11
11 1
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
2/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
. . . hängt vom Betrachter ab
11
1 1
1 1 1 1
11
11
11
11
11
11
1 1 1
paradox?
1
11
11
11
11
11
11
11
11
11
11
11 1
111
11
11
11
11
11
11
11
11
11 1
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
2/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Übersicht
• Gefahr und Reiz logischer Diagonalen“
”
• Diagonalisierung über Mengen
• Diagonalisierung über Algorithmen
• Diagonalisierung über formale Systeme
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
3/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Übersicht
• Gefahr und Reiz logischer Diagonalen“
”
Epimenides (7.Jh.v.Chr.)
• Diagonalisierung über Mengen
Cantor (1845–1918), Russell (1872–1970)
• Diagonalisierung über Algorithmen
Turing (1912–1954)
• Diagonalisierung über formale Systeme
Gödel (1906–1978)
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
3/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Teil I: Ein Beispiel logischer Diagonalisierung
überlieferte Quelle: Epimenides, Kreta, 7.Jh.v.Chr.
Voraussetzungen (klassische Logik):
• Aussagen entweder wahr oder falsch
• Wahrheitswerte 1 (wahr) 0 (falsch)
Wir betrachten Aussagen, die über andere Aussagen sprechen:
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
4/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Teil I: Ein Beispiel logischer Diagonalisierung
überlieferte Quelle: Epimenides, Kreta, 7.Jh.v.Chr.
Voraussetzungen (klassische Logik):
• Aussagen entweder wahr oder falsch
• Wahrheitswerte 1 (wahr) 0 (falsch)
Wir betrachten Aussagen, die über andere Aussagen sprechen:
(A): (B) ist wahr.
A sagt dasselbe wie B“
”
2010
Martin Otto
(A ≡ B)
Diagonalen, die den Rahmen sprengen
4/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Teil I: Ein Beispiel logischer Diagonalisierung
überlieferte Quelle: Epimenides, Kreta, 7.Jh.v.Chr.
Voraussetzungen (klassische Logik):
• Aussagen entweder wahr oder falsch
• Wahrheitswerte 1 (wahr) 0 (falsch)
Wir betrachten Aussagen, die über andere Aussagen sprechen:
(A): (B) ist wahr.
A sagt dasselbe wie B“
”
2010
Martin Otto
(A ≡ B)
Diagonalen, die den Rahmen sprengen
AB 0 1
0 X #
1 # X
4/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Teil I: Ein Beispiel logischer Diagonalisierung
überlieferte Quelle: Epimenides, Kreta, 7.Jh.v.Chr.
Voraussetzungen (klassische Logik):
• Aussagen entweder wahr oder falsch
• Wahrheitswerte 1 (wahr) 0 (falsch)
Wir betrachten Aussagen, die über andere Aussagen sprechen:
(A): (B) ist falsch.
A sagt das genaue Gegenteil von B“
”
2010
Martin Otto
(A 6≡ B)
Diagonalen, die den Rahmen sprengen
4/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Teil I: Ein Beispiel logischer Diagonalisierung
überlieferte Quelle: Epimenides, Kreta, 7.Jh.v.Chr.
Voraussetzungen (klassische Logik):
• Aussagen entweder wahr oder falsch
• Wahrheitswerte 1 (wahr) 0 (falsch)
Wir betrachten Aussagen, die über andere Aussagen sprechen:
(A): (B) ist falsch.
A sagt das genaue Gegenteil von B“
”
2010
Martin Otto
(A 6≡ B)
Diagonalen, die den Rahmen sprengen
AB 0 1
0 # X
1 X #
4/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Diagonalisierung:
Epimenides’ Lügner
(A) : (B) ist wahr.
(B) : (A) ist falsch.
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
5/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Diagonalisierung:
Epimenides’ Lügner
(A) : (B) ist wahr.
(B) : (A) ist falsch.
AB 0 1
0 # #
1 # #
A ≡ B 6≡ A
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
5/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Diagonalisierung:
Epimenides’ Lügner
(A) : (B) ist wahr.
(B) : (A) ist falsch.
AB 0 1
0 # #
1 # #
A ≡ B 6≡ A
(A) : (A) ist falsch.
Diese Aussage ist falsch.“
”
A besagt sein eigenes Gegenteil“, A 6≡ A
”
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
5/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Diagonalisierung:
Epimenides’ Lügner
(A) : (B) ist wahr.
(B) : (A) ist falsch.
AB 0 1
0 # #
1 # #
A ≡ B 6≡ A
(A) : (A) ist falsch.
Diese Aussage ist falsch.“
”
A besagt sein eigenes Gegenteil“, A 6≡ A
”
A ist nicht bloß falsch, sondern sinnlos;
vielleicht garkeine Aussage?
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
5/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Welcher Rahmen wird hier gesprengt?
Gesprengt:
• die Welt einfacher logischer Aussagen
mit konsistenter Wahrheitsbewertung
Problematisch (im Gegensatz zu harmloseren Aussagen):
• innerer Bezug auf den Wahrheitswert der gesamten Aussage
(A) : . . . (A) . . .
2010
Martin Otto
Diese Aussage“
”
Diagonalen, die den Rahmen sprengen
6/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Welcher Rahmen wird hier gesprengt?
. . . und wodurch?
Gesprengt:
• die Welt einfacher logischer Aussagen
mit konsistenter Wahrheitsbewertung
Problematisch (im Gegensatz zu harmloseren Aussagen):
• innerer Bezug auf den Wahrheitswert der gesamten Aussage
(A) : . . . (A) . . .
Diese Aussage“
”
Selbstbezüglichkeit
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
6/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Teil II: Diagonalisierung über Mengen
Georg Cantor (1845–1918)
2010
Martin Otto
Bertrand Russell (1872–1970)
Diagonalen, die den Rahmen sprengen
7/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Teil II: Diagonalisierung über Mengen
Georg Cantor (1845–1918)
Begriffe der elementaren Mengenlehre:
a ∈ M: a ist Element der Menge M;
A ⊆ M: A ist Teilmenge von M;
A := {a ∈ M : a hat Eigenschaft E } ⊆ M,
die durch E definierte Teilmenge von M.
2010
Martin Otto
•b
•
A
Diagonalen, die den Rahmen sprengen
•a
•
•
•
M
7/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Drei Fragen zu Mengen:
(1): Wieviele Teilmengen hat eine n-elementige Menge?
(2): Wieviele Teilmengen hat die (unendliche)
Menge der natürlichen Zahlen N = {0, 1, 2, 3, . . .}?
(3): Kann es eine/die Menge aller Mengen geben?
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
8/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
(1): Wieviele Teilmengen hat eine n-elementige Menge?
das wisst ihr!
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
9/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
(1): Wieviele Teilmengen hat eine n-elementige Menge?
das wisst ihr!
Erinnerung: Eine Teilmenge A ⊆ M besteht
ausschließlich aus Elementen von M
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
9/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
(1): Wieviele Teilmengen hat eine n-elementige Menge?
das wisst ihr!
Erinnerung: Eine Teilmenge A ⊆ M besteht
ausschließlich aus Elementen von M
Beispiel:
2010
M = {1, 2, 3, 4, 5} hat fünf Elemente
und wieviele Teilmengen?
Martin Otto
Diagonalen, die den Rahmen sprengen
9/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
(1): Wieviele Teilmengen hat eine n-elementige Menge?
das wisst ihr!
Erinnerung: Eine Teilmenge A ⊆ M besteht
ausschließlich aus Elementen von M
Beispiel:
M = {1, 2, 3, 4, 5} hat fünf Elemente
und wieviele Teilmengen?
Antwort: 2n
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
9/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
(2): Wieviele Teilmengen hat die Menge N = {0, 1, 2, . . .}
→ Cantor
was heißt hier ‘wieviele’ ?
Wir wollen uns überzeugen, dass es keine vollständige Aufzählung
aller Teilmengen A ⊆ N geben kann:
Zu jeder (unendlichen) Liste von Teilmengen A0 , A1 , A2 , . . . von N
gibt es mindestens eine Teilmenge A ⊆ N,
die in dieser Liste nicht vorkommt!
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
10/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
(2): Wieviele Teilmengen hat die Menge N = {0, 1, 2, . . .}
→ Cantor
was heißt hier ‘wieviele’ ?
Wir wollen uns überzeugen, dass es keine vollständige Aufzählung
aller Teilmengen A ⊆ N geben kann:
Zu jeder (unendlichen) Liste von Teilmengen A0 , A1 , A2 , . . . von N
gibt es mindestens eine Teilmenge A ⊆ N,
die in dieser Liste nicht vorkommt!
Beweis durch Diagonalisierung:
Wir beschreiben anhand einer gegebenen Liste A0 , A1 , A2 , . . . eine
Teilmenge A, die von allen An verschieden ist:
A := {n ∈ N : n 6∈ An }
Dann ist n ∈ A genau dann, wenn n 6∈ An ;
also ist A 6= An .
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
10/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Das Diagonalisierungs-Argument
0
1
A0 X ×
2
3
4
5
X X
×
X X X
A1 X X X X X
A2
A3
A4
..
.
A
2010
×
6
×
7
...
×
× X × X X X
× × × X × X × X
× × X × × X × X
×
×
×
×
Martin Otto
X
×
X
Diagonalen, die den Rahmen sprengen
11/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Das Diagonalisierungs-Argument
0
1
A0 X ×
2
3
4
5
X X
×
X X X
A1 X X X X X
2010
A2
×
× × X
A3
×
×
× X ×
A4
..
.
×
×
X
A
× × X × X
Martin Otto
×
×
6
×
7
...
×
X X X
X
×
X
× × X
×
X
Diagonalen, die den Rahmen sprengen
12/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Konsequenzen
• Es muss Teilmengen A ⊆ N geben, die durch
keine (aufschreibbare) Eigenschaft definierbar sind.
• Es gibt unterschiedliche Grade von Unendlichkeit;
genau wie die Menge aller Teilmengen von N,
ist R (die Menge der reellen Zahlen) viel unendlicher“ als N,
”
während Q, Z und N auf der gleichen Stufe stehen (Cantor).
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
13/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
(3): Es kann keine Menge aller Mengen geben!
→ Russell
Wäre A die Menge aller Mengen, so müsste A ∈ A sein
(aber das schreckt uns noch nicht).
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
14/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
(3): Es kann keine Menge aller Mengen geben!
→ Russell
Wäre A die Menge aller Mengen, so müsste A ∈ A sein
(aber das schreckt uns noch nicht).
Wir sehen auf
B := {M ∈ A : M 6∈ M}
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
14/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
(3): Es kann keine Menge aller Mengen geben!
→ Russell
Wäre A die Menge aller Mengen, so müsste A ∈ A sein
(aber das schreckt uns noch nicht).
Wir sehen auf
B := {M ∈ A : M 6∈ M}
Was gilt: B ∈ B oder B 6∈ B?
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
14/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
(3): Es kann keine Menge aller Mengen geben!
→ Russell
Wäre A die Menge aller Mengen, so müsste A ∈ A sein
(aber das schreckt uns noch nicht).
Wir sehen auf
B := {M ∈ A : M 6∈ M}
Was gilt: B ∈ B oder B 6∈ B?
B∈B
Wir finden:
beides unmöglich!
B 6∈ B
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
→ Lügner
14/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
(3): Es kann keine Menge aller Mengen geben!
→ Russell
Wäre A die Menge aller Mengen, so müsste A ∈ A sein
(aber das schreckt uns noch nicht).
Wir sehen auf
B := {M ∈ A : M 6∈ M}
Was gilt: B ∈ B oder B 6∈ B?
B∈B
Wir finden:
beides unmöglich!
B 6∈ B
→ Lügner
Es folgt, dass A als Menge nicht existiert!
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
14/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
(3): Es kann keine Menge aller Mengen geben!
→ Russell
Wäre A die Menge aller Mengen, so müsste A ∈ A sein
(aber das schreckt uns noch nicht).
Wir sehen auf
B := {M ∈ A : M 6∈ M}
Was gilt: B ∈ B oder B 6∈ B?
B∈B
Wir finden:
beides unmöglich!
B 6∈ B
→ Lügner
Es folgt, dass A als Menge nicht existiert!
“A vanishes in a puff of logic”
Hitchhiker’s Guide to the Galaxy
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
14/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Teil III: Diagonalisierung über Algorithmen/Programme
Alan Turing (1912–1954)
und das Halteproblem“ als Quelle
”
vieler Unmöglichkeitsbeweise
Algorithmus = Berechnungsverfahren/Lösungsverfahren
Al Chwarismi (∼ 800)
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
15/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Teil III: Diagonalisierung über Algorithmen/Programme
Alan Turing (1912–1954)
und das Halteproblem“ als Quelle
”
vieler Unmöglichkeitsbeweise
Algorithmus = Berechnungsverfahren/Lösungsverfahren
Al Chwarismi (∼ 800)
2010
Martin Otto
Alan Turing (1912–1954)
Diagonalen, die den Rahmen sprengen
15/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Algorithmen/Berechnungsverfahren
können viele Entscheidungsprobleme lösen, z.B.:
Zu gegebenem n ∈ N:
Ist n gerade?
Zu gegebenen k, m, n ∈ N:
Ist k ∗ m = n?
Zu gegebenem Sudoku S:
Ist S lösbar?
Zu gegebener Schach-Position:
Kann Weiß Gewinn erzwingen?
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
16/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Gibt es (sinnvoll gestellte, mathematische) Probleme,
die prinzipiell nicht durch Algorithmen zu lösen sind?
Verfahren/Programme/Computer
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
Kreativität?
17/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Gibt es (sinnvoll gestellte, mathematische) Probleme,
die prinzipiell nicht durch Algorithmen zu lösen sind?
Verfahren/Programme/Computer
Kreativität?
Annahmen:
• Verfahren V sind als Texte (Programme) hV i kodiert und
anhand der kodierten Fassung auf Eingaben ausführbar.
• Um ein Entscheidungsproblem zu lösen, muss ein Verfahren auf
jede (zulässige) Eingabe nach endlich vielen Schritten korrekt
JA oder NEIN antworten (jedenfalls terminieren/anhalten).
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
17/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Gibt es (sinnvoll gestellte, mathematische) Probleme,
die prinzipiell nicht durch Algorithmen zu lösen sind?
Verfahren/Programme/Computer
Kreativität?
Annahmen:
• Verfahren V sind als Texte (Programme) hV i kodiert und
anhand der kodierten Fassung auf Eingaben ausführbar.
• Um ein Entscheidungsproblem zu lösen, muss ein Verfahren auf
jede (zulässige) Eingabe nach endlich vielen Schritten korrekt
JA oder NEIN antworten (jedenfalls terminieren/anhalten).
Ein gefährlich klingendes Entscheidungsproblem:
Zu gegebenen Verfahren V , W :
Hält V auf Eingabe hW i schließlich an?
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
17/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Halteproblem: Diagonalisierung
Nützliche Variante (→ Selbstreferenz, Lügner, Russell):
Zu gegebenen Verfahren V:
Hält V auf Eingabe hVi schließlich an?
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
(H)
18/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Halteproblem: Diagonalisierung
Nützliche Variante (→ Selbstreferenz, Lügner, Russell):
Zu gegebenen Verfahren V:
Hält V auf Eingabe hVi schließlich an?
(H)
Annahme, Verfahren T löst dieses Entscheidungsproblem H:
Für jedes V liefert T auf Eingabe hV i
NEIN falls V auf hV i nicht anhält.
JA
falls V auf hV i schließlich anhält.
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
18/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Halteproblem: Diagonalisierung
Nützliche Variante (→ Selbstreferenz, Lügner, Russell):
Zu gegebenen Verfahren V:
Hält V auf Eingabe hVi schließlich an?
(H)
Annahme, Verfahren T löst dieses Entscheidungsproblem H:
Für jedes V liefert T auf Eingabe hV i
NEIN falls V auf hV i nicht anhält.
JA
falls V auf hV i schließlich anhält.
Wir könnten dann T etwas umbauen zu T 0 :
nicht-terminierende Schleife statt Antwort JA“
”
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
18/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Halteproblem: Diagonalisierung
Nützliche Variante (→ Selbstreferenz, Lügner, Russell):
Zu gegebenen Verfahren V:
Hält V auf Eingabe hVi schließlich an?
(H)
Annahme, Verfahren T löst dieses Entscheidungsproblem H:
Für jedes V liefert T 0 auf Eingabe hV i
NEIN falls V auf hV i nicht anhält.
∞
falls V auf hV i schließlich anhält.
Wir könnten dann T etwas umbauen zu T 0 :
nicht-terminierende Schleife statt Antwort JA“
”
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
18/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Halteproblem: Diagonalisierung
Wenn es ein Verfahren zur Lösung von H gäbe,
dann auch ein Verfahren T 0 :
Für jedes V liefert T 0 auf Eingabe hV i
NEIN falls V auf hV i nicht anhält.
∞
falls V auf hV i schließlich anhält.
Was liefert dieses T 0 auf Eingabe hT 0 i?
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
19/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Halteproblem: Diagonalisierung
Wenn es ein Verfahren zur Lösung von H gäbe,
dann auch ein Verfahren T 0 :
Für jedes V liefert T 0 auf Eingabe hV i
NEIN falls V auf hV i nicht anhält.
∞
falls V auf hV i schließlich anhält.
Was liefert dieses T 0 auf Eingabe hT 0 i?
NEIN falls T 0 auf hT 0 i nicht anhält.
∞
falls T 0 auf hT 0 i schließlich anhält.
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
#
19/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Halteproblem: Diagonalisierung
Wenn es ein Verfahren zur Lösung von H gäbe,
dann auch ein Verfahren T 0 :
Für jedes V liefert T 0 auf Eingabe hV i
NEIN falls V auf hV i nicht anhält.
∞
falls V auf hV i schließlich anhält.
Was liefert dieses T 0 auf Eingabe hT 0 i?
NEIN falls T 0 auf hT 0 i nicht anhält.
∞
falls T 0 auf hT 0 i schließlich anhält.
#
Auf Eingabe hT 0 i kann T 0 weder anhalten noch nicht anhalten;
Es kann also kein solches T 0 geben, also auch kein T .
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
19/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Halteproblem: Diagonalisierung
Wenn es ein Verfahren zur Lösung von H gäbe,
dann auch ein Verfahren T 0 :
Für jedes V liefert T 0 auf Eingabe hV i
NEIN falls V auf hV i nicht anhält.
∞
falls V auf hV i schließlich anhält.
Was liefert dieses T 0 auf Eingabe hT 0 i?
NEIN falls T 0 auf hT 0 i nicht anhält.
∞
falls T 0 auf hT 0 i schließlich anhält.
#
Auf Eingabe hT 0 i kann T 0 weder anhalten noch nicht anhalten;
Es kann also kein solches T 0 geben, also auch kein T .
. . . vanishes in a puff of logic
Fazit: H ist durch keinen Algorithmus lösbar.
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
19/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Konsequenzen aus Unlösbarkeit des Halteproblems
Viele andere Probleme erben die prinzipielle
algorithmische Unlösbarkeit vom Halteproblem, z.B.:
Zu gegebenen Programmen P1 , P2 :
Liefern P1 und P2 auf allen Eingaben dasselbe Ergebnis?
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
20/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Konsequenzen aus Unlösbarkeit des Halteproblems
Viele andere Probleme erben die prinzipielle
algorithmische Unlösbarkeit vom Halteproblem, z.B.:
Zu gegebenen Programmen P1 , P2 :
Liefern P1 und P2 auf allen Eingaben dasselbe Ergebnis?
Zu gegebener Menge von Kacheln mit gefärbten Rändern:
Kann man damit beliebig große Quadrate kacheln?
•
•
•
•
•
Beispiel: ••1 •, ••2 •, ••3 •, ••4 •, ••5 •
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
20/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Konsequenzen aus Unlösbarkeit des Halteproblems
Viele andere Probleme erben die prinzipielle
algorithmische Unlösbarkeit vom Halteproblem, z.B.:
Zu gegebenen Programmen P1 , P2 :
Liefern P1 und P2 auf allen Eingaben dasselbe Ergebnis?
Zu gegebener Menge von Kacheln mit gefärbten Rändern:
Kann man damit beliebig große Quadrate kacheln?
•
•
•
•
•
Beispiel: ••1 •, ••2 •, ••3 •, ••4 •, ••5 •
−→
• • • •
•2• •5• •2• •5•
• • • •
• • • •
•3• •1• •3• •1•
• • • •
• • • •
•2• •5• •2• •5•
• • • •
• • • •
•3• •1• •3• •1•
• • • •
u.v.a. Fragen aus allen möglichen Bereichen der Mathematik
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
20/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Teil IV, Ausblick: Gödels Unvollständigkeits-Beweis
oder: es kommt noch schlimmer
Kurt Gödel (1906–1978)
rechts: Albert Einstein
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
21/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Gödels Unvollständigkeitsbeweis
Epimenides’ Lügner: (A): Aussage (A) ist nicht wahr“
”
Gödels Aussage: (G): Aussage (G) ist nicht beweisbar“
”
mit Bezug auf Beweisbarkeit
in einem (vernünftigen) formalen System
(mathematischer Beweiskalkül + Axiomensystem)
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
22/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Gödels Unvollständigkeitsbeweis
Epimenides’ Lügner: (A): Aussage (A) ist nicht wahr“
”
Gödels Aussage: (G): Aussage (G) ist nicht beweisbar“
”
mit Bezug auf Beweisbarkeit
in einem (vernünftigen) formalen System
(mathematischer Beweiskalkül + Axiomensystem)
Dann ergibt sich zwar kein Widerspruch, aber dass
(G) wahr und tatsächlich nicht beweisbar ist!
→
2010
prinzipielle Unvollständigkeit/Offenheit der Mathematik
Martin Otto
Diagonalen, die den Rahmen sprengen
22/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Diagonalisierung
Selbstbezüglichkeit als Quelle
• verblüffender Konstruktionen
• überraschender Unmöglichkeitsbeweise
• nachweisbarer prinzipieller Grenzen
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
23/23
Mathe-Olympiade Hessen 2010 // TU Darmstadt
Diagonalisierung
Selbstbezüglichkeit als Quelle
• verblüffender Konstruktionen
• überraschender Unmöglichkeitsbeweise
• nachweisbarer prinzipieller Grenzen
Unentscheidbarkeit und Unvollständigkeit
sind Grundphänomene der Mathematik
Mathematik und Meta-Mathematik in der mathematischen Logik
2010
Martin Otto
Diagonalen, die den Rahmen sprengen
23/23