als PDF

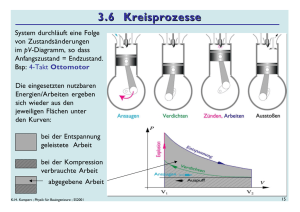
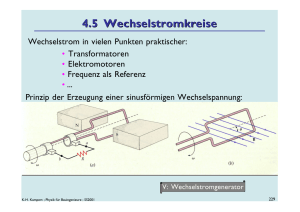
4.4 Induktion
Bisher: Strom durch einen Draht → Magnetfeld
Jetzt: zeitlich veränderliches Magnetfeld → Strom
Spannungen und Ströme, die durch Veränderungen von Magnetfeldern entstehen, bezeichnet man als Induktionsspannungen, bzw.
Induktionsströme.
Den Vorgang bezeichnet man als magnetische Induktion.
r r
r r
[Φ] = Weber
Magnetischer Fluss: Φ = ∫ B ⋅ dA bzw.: dΦ = B ⋅ dA
1 Wb = 1 T ⋅ m 2
(
)
A
Induzierte Spannung: Uind
dΦ
=−
dt
Faradaysches Gesetz:
Jede zeitl. Änderung des magn.
Flusses induziert eine elektr.
Spannung
Bei einer Spule mit N Windungen: Uind
K-H. Kampert ; Physik für Bauingenieure ; SS2001
dΦ
= −N
dt
209
Lenzsche Regel & Induktionsstrom
Zum Vorzeichen:
Nach der Lenzschen Regel ist die Induktionsspannung der
Ursache der Induktion entgegengesetzt gerichtet.
(Bewegungshemmende Wirkung)
V: Lenzsche Regel
Bsp:
S
N
Der induzierte Strom im Ring erzeugt ein Magnetfeld, welches
dem ursprünglichen Magnetfeld des Stabes entgegengesetzt
gerichtet ist ➳ Schwächung des erregenden B-Feldes
(Sonst wäre ein Perpetuum Mobile möglich!)
V: Induktion
K-H. Kampert ; Physik für Bauingenieure ; SS2001
210
Selbstinduktion
Stabmagnet wird nun durch eine Spule ersetzt :
Einschaltung der Spule
➳ Erzeugung einer Induktionsspannung in der gleichen Spule.
Diese ist dem zunehmenden Feld entgegengesetzt.
Betrachte Spule mit der
N
Windungszahl N und der Länge l: B = µ0 ⋅ I ⋅ l
Magnetischer Fluss:
N
N2 ⋅ A
Φ mag = B ⋅ N ⋅ A = µ0 ⋅ I ⋅ ⋅ N ⋅ A = µ0 ⋅ I ⋅
l
l
„Anzahl der Feldlinien“, die die Fläche A
durchkreuzen; In der Spule: N·A
Φ mag
N 2 ⋅ A Induktivität einer Spule
⇒ L=
= µ0 ⋅
2
Wb
T
⋅
m
Vs
I
l
=
=
[ L] = [Henry] =
A
A
A
K-H. Kampert ; Physik für Bauingenieure ; SS2001
211
Selbstinduktion (2)
Φ
Mit L =
lässt sich die induzierte Spannung schreiben als:
I
Uind
dΦ
dI
=−
= −L ⋅
dt
dt
Die Selbstinduktionsspannung ist somit proportional zur
zeitlichen Änderung des Stroms.
Versuch
Einschaltverzögerung
in (2) durch Gegenspannung in der Spule
K-H. Kampert ; Physik für Bauingenieure ; SS2001
1
≈
≈
2
≈
Spannungsstoß beim
Abschalten bringt Birne
zum Leuchten
212
Selbstinduktion - ein Beispiel
Eine Zylinderspule mit 800 Windungen hat die Länge 40 cm
und einen Durchmesser von 50 cm.
Der Strom werde innerhalb von 0.1 Sekunden gleichmäßig von
0.1 A auf 5 A erhöht.
Welche Spannung wird in einer induktiv gekoppelten innen
liegenden Sekundärspule mit 2000 Windungen induziert?
Φ = B⋅ A
N1=800 ; N2=2000
Uind
∆Φ
∆B
µ 0 N1 ∆I
= − N2
= −N2 A
= −N2 A
∆t
∆t
l ∆t
Uind
1.25 ⋅ 10 −6 Vs Am ⋅ 800 4.9A
= −48.1 V
= −2000 ⋅ 0, 25 m ⋅ π ⋅
0.4 m
0.1s
2
K-H. Kampert ; Physik für Bauingenieure ; SS2001
2
213
Wirbelstr öme (1)
Was geschieht mit Induktionsströmen in ausgedehnten
leitenden Körpern?
V
W
U
B-Feld
u
Bewegung erzeugt nach
der 3-Finger Regel einen
Strom im B-Feldbereich
nach rechts
Strom fließt über den
feldfreien Raum zurück,
d.h. Wirbelstrom
Die Erregung des Wirbelstrom hemmt nach
der Lenzschen Regel die Bewegung nach unten.
V: Waltenhofensche Pendel
K-H. Kampert ; Physik für Bauingenieure ; SS2001
214
Wirbelstr öme (2)
Der beschriebene Effekt ist z.B. bei Wirbelstrombremsen
erwünscht,
aber in Transformatoren oder Elektromotoren unerwünscht!
Lsg.: Verwendung laminierter Bleche
d.h.: Einbringung von Schlitzen
Effekt: Stromfluss wird unterbrochen
B-Feld
u
K-H. Kampert ; Physik für Bauingenieure ; SS2001
215
Magnetfelder in Materie: Ferromagnetismus
Induktionswirkungen, Magnetkräfte, etc. werden davon
beeinflusst, ob sich Materie im Magnetfeld befindet:
r
r
B( mit Stoff )
mr : Permeabilitätszahl
B = µ0 ⋅ µr ⋅ H ; µr =
B(ohne Stoff ) m0·mr : Permeabilität
Ferromagnetische Stoffe (z.B. Eisen, Kobalt, Nickel) zeigen eine
besonders große Wirkung: mr à 1
Ursache: Weißsche Bezirke
Innerhalb eines W.-Bezirks jeweils
gleiche Ausrichtung der magnetischen
Momente.
K-H. Kampert ; Physik für Bauingenieure ; SS2001
Effekt wird aufgehoben durch Erhitzung
über die Curie-Temperatur,
darüber mr t 1 (Paramagnetisch)
TCurie (Fe) = 1040 °C
TCurie (Co) = 1400 °C
TCurie (Ni) = 370 °C
216
Ferromagnetika in der Praxis (1)
Aufnahme eines Fe-3%Si-Kristalls mit
einem Raster-Elektronen-Mikroskop
mit Polarisationsanalyse:
Die jeweiligen Farben entsprechen
den vier möglichen Orientierungen
der Weißschen Bezirke.
Magnetische Feldlinien auf einem
bespielten Tonband
aus Kobalt.
K-H. Kampert ; Physik für Bauingenieure ; SS2001
217
Ferromagnetika in der Praxis (2)
10 µm
Festplatte (Seagate)
K-H. Kampert ; Physik für Bauingenieure ; SS2001
218
Dia- und Para- und Ferromagnetismus
Stoffe werden hinsichtlich ihrer Permeabilität in drei Gruppen eingeteilt:
Diamagnetisch: mr d 1, d.h. Feldlinien werden herausgedrängt
ï B-Feld wird geschwächt, Material wird abgestoßen
Ursache: äußeres Feld induziert magnetische Momente im Stoff,
diese sind nach der Lenzschen Regel dem Feld entgegengesetzt
Bsp: Kupfer mr = 0.999 990 3, Silber, Kohlenstoff, Bismut
Paramagnetisch: mr t 1, d.h. Feldlinien werden hineingezogen
ï B-Feld wird gestärkt, Material wird angezogen
Ursache: Atome haben permanente magnetische Momente
Bsp: Sauerstoff (20 °C) mr = 1.000 001 9, Aluminium, Platin, Mangan
Ferromagnetisch: mr p 1 ï B-Feld wird sehr stark erhöht
Material wird sehr stark angezogen
Ursache: Weißsche Bezirke
Bsp: Eisen, Aluminium, Platin, Mangan; mr > 5000 - 100 000
K-H. Kampert ; Physik für Bauingenieure ; SS2001
219
Hysterese bei Ferromagneten
Bei ferromagnetischen Stoffen ist die Permeabilitätszahl
abhängig von der Feldstärke. Sie hängt außerdem von der
Vorbehandlung des Stoffes ab.
alle Weißschen Bezirke || B
I
Fläche der Kurve
U Energie, die zum Ummagnetisieren
erforderlich ist.
...sollte für Transformatoren also
möglichst klein sein ➔ „Weicheisen“,
für Dauermagneten dagegen
möglichst groß ➔ „Harteisen“
K-H. Kampert ; Physik für Bauingenieure ; SS2001
220
Bsp . Dynamoblech
Neukurve
1 dB
⋅
µr =
µ0 dH
Berechnung von
mr aus den
Wertepaaren von B vs H
K-H. Kampert ; Physik für Bauingenieure ; SS2001
221
Energie- und Energiedichte des Magnetfeldes (1)
Wir haben beobachtet, dass sich der elektrische Strom beim
Einschalten einer Spule verzögert.
Ursache war die entgegen gesetzte Selbstinduktionsspannung,
die beim Aufbau des B-Feldes auftritt.
Nach Beendigung ist Energie in Form des B-Feldes gespeichert.
Diese wird beim Abschalten auf analoge Weise wieder freigesetzt.
Elektrische Leistung:
dEel
Pel =
= Uind ⋅ I
dt
Uind = −
dΦ mag
dt
dI
= −L ⋅
dt
dEel
dI
⇒
= −L ⋅ ⋅ I
dt
dt
I
⇒ Eel = L ⋅ ∫ i ⋅ di
0
K-H. Kampert ; Physik für Bauingenieure ; SS2001
⇒ dEel = L ⋅ dI ⋅ I (Betrag)
Vgl. Kondensator
1
1
2
⇒ Eel = L ⋅ I 2 =! Emag
E
=
C
⋅
U
C
2
2
222
Energie- und Energiedichte des Magnetfeldes (2)
Feldvolumen in einer Zylinderspule: V = A ⋅ l
⇒
Emag
2

1
1
⋅ A 2
N
2
= L ⋅ I = ⋅  µ0 ⋅ µr ⋅
⋅I
2
2 
l 
L
N
H = I⋅
l
1
1
N
⋅ I ⋅ N ⋅ A = B⋅ H ⋅l ⋅ A
= µ0 ⋅ µr ⋅ I ⋅


2
l
2
B
Energiedichte:
Emag 1
B
H=
= B⋅ H
Wmag =
µ0 ⋅ µr
2
V
1
=
B2
2 ⋅ µ0 ⋅ µr
K-H. Kampert ; Physik für Bauingenieure ; SS2001
⇒
Emag =
1
B⋅ H ⋅V
2
1
Vgl.: Eelek = E ⋅ D ⋅ V
2
223
Anwendung: Elektromotoren & Generatoren
Bsp. eines Gleichstrommotors: Linearmotor (siehe Übungsaufgabe)
r r
r
F = I ⋅l × B
l : Länge des Leiters
im B-Feld
Drehmoment: M = F ⋅ a ⋅ sin α
⇒ M = I ⋅ l ⋅ B ⋅ a ⋅ sin α
r
r
(l immer ⊥ B)
l ⋅ a = Fläche der Leiterschleife im B - Feld
I ⋅ l ⋅ a = magn. Diplomoment
Nachteil dieser Konstruktion:
Motor würde in der Senkrechtposition des Ankers stehen bleiben
K-H. Kampert ; Physik für Bauingenieure ; SS2001
224
Anwendung: Elektromotoren & Generatoren
Bsp. eines Gleichstrommotors: Linearmotor (siehe Übungsaufgabe)
r r
r
F = I ⋅l × B
l : Länge des Leiters
im B-Feld
Drehmoment: M = F ⋅ a ⋅ sin α
⇒ M = I ⋅ l ⋅ B ⋅ a ⋅ sin α
r
r
(l immer ⊥ B)
l ⋅ a = Fläche der Leiterschleife im B - Feld
I ⋅ l ⋅ a = magn. Diplomoment
Nachteil dieser Konstruktion:
Motor würde in der Senkrechtposition des Ankers stehen bleiben
Abhilfe: mehrere Anker
K-H. Kampert ; Physik für Bauingenieure ; SS2001
225
Anwendung: Elektromotoren & Generatoren
Weitere logische Verbesserung: Viele Anker
Motor läuft „rund“
–
+
Maximale Rotationsfrequenz
durch induzierte Gegenspannung
begrenzt.
(Analog zum Linearmotor)
V: Gleichstrommotor & Generator
K-H. Kampert ; Physik für Bauingenieure ; SS2001
226
Bsp : PKW Anlasser
6) Bürste
7) Kommutator
10) Anker
K-H. Kampert ; Physik für Bauingenieure ; SS2001
227
PKW Anlasser
Kap. 4.5
K-H. Kampert ; Physik für Bauingenieure ; SS2001
7,8) Kommutator
10) Anker
228