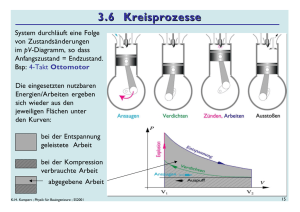
3.5 Zustandsänderung von Gasen

3.5 Zustandsänderung von Gasen
Ziel:
Besprechung der thermodynamischen Grundlagen von
Wärmekraftmaschinen und Wärmepumpen
Zustand von Gasen wird durch
• Druck p,
• Volumen V, und
• Temperatur T
beschrieben
Zustandsänderungen
• isochor
• isobar
• isotherm
• adiabatisch
K-H. Kampert ; Physik für Bauingenieure ; SS2001
thermodyn. Zustandsgrößen
sind auf vier verschiedene Arten möglich:
(Volumen konstant)
Energieaustausch
(Druck konstant)
mit Umgebung
(Temperatur konstant)
(kein Wärmeaustausch mit Umgebung)
1
pV-Diagramm
p
isochor
isobar
~1/V
V
isotherm: p·V=const (Vgl. Boyle Mariotte)
adiabatisch: p·V/ T=const
(Abkühlung bei der Expansion
bewirkt verstärkte Druckabnahme)
Prinzip der Energieerhaltung
bei Zustandsänderungen führt zum...
K-H. Kampert ; Physik für Bauingenieure ; SS2001
2
1. Hauptsatz der Wärmelehre
Bei Zufuhr von Wärme DQ kann Gas die innere Energie DU erhöhen
und mechanische Arbeit DW leisten:
DQ = DU + DW
Vorzeichenkonvention:
DQ > 0 : dem Gas zugeführte Wärme
DQ < 0 : vom Gas abgegebene Wärme
DW < 0 : dem Gas zugeführte mechanische Arbeit
DW > 0 : vom Gas abgegebene mechanische Arbeit
Bsp: Gas dehnt sich bei konstantem Druck p aus
fl das Gas leistet mechanische Arbeit zur Vergrößerung des Volumens
Arbeit = Kraft · Weg = F·Ds = (p·A) · Ds = (p·A) · DV/A = p · DV
fl DW = p · DV
K-H. Kampert ; Physik für Bauingenieure ; SS2001
fl W = ∫ p(V) · dV
Vorzeichen lt.
Konvention oben
3
Erläuterung der inneren Energie U:
Isochore Zustandsänderung
V sei konstant, während die Wärmemenge DQ zugeführt wird,
d.h.: DV = 0 fl DW = 0 fl DQ = DU + DW = DU
Die zugeführte Wärmemenge DQ wird also allein zur Erhöhung
der inneren Energie des Gases verwendet
Hierfür gilt:
DQ = cv · m · DT fl DU = cv · m · DT
Wichtiges Ergebnis:
Die innere Energie eines idealen Gases
wird allein von der Temperatur bestimmt.
p
p2
p1
DQ = Q1,2 = cv · m · (T2-T1) ; DW = 0
K-H. Kampert ; Physik für Bauingenieure ; SS2001
T2
T1
V
4
Isobare Zustandsänderung
Wärmemenge DQ wird bei konstantem Druck zugeführt
fl Volumenänderung
p
DQ = DU + DW
T2
T1
DW
V1
= p·DV
= cv · m · DT
= cp · m · DT
V2
V
ï
DW=p·DV
cp · m · DT = cv · m · DT + p·DV
‹ m · (cp - cv) · DT = p · DV
bzw. m · (cp - cv) · T = p · V
Vergleiche mit Zustandsgl.: m · R s · T = p · V
ï
K-H. Kampert ; Physik für Bauingenieure ; SS2001
R s = cp - cv
Mayersche Gleichung
5
Isotherme Zustandsänderung
Gastemperatur muss während der Zustandsänderung konstant gehalten
werden fl Kontakt mit Wärmebad erforderlich
DQ = DU + DW
p
DQ = p · DV = DW
T1
DW
V1
Weitere Auswertung erfordert Kenntnis
p = p(V):
V2 V
verwende Zustandsgl.: p · V = m · R s · T
Einsetzen: DW = p · DV = ( m · R s · T / V ) · DV
V2
V
p
dV
= m ⋅ Rs ⋅ T ⋅ ln 2 = m ⋅ Rs ⋅ T ⋅ ln 1
V1
p2
V
V1
1
Beachte Vorzeichen: V2 > V1 fl Gas leistet Arbeit
p∝
d.h. W1,2 > 0
V
K-H. Kampert ; Physik für Bauingenieure ; SS2001
Integrieren: W1, 2 = m ⋅ Rs ⋅ T ⋅ ∫
6
Wiederholung vom 10.5.01
Zustandsänderungen von Gasen: isobar, ischor, isotherm, adiabatisch
Alle Prozesse werden durch den
1. Hauptsatz der Wärmelehre beschrieben:
DQ = DU + DW
mechanische Arbeit: DW=W12 = p · DV bzw. fl W = ∫ p(V) · dV
isochor: DV = 0 fl DW = 0 fl DU = cv · m · DT
p
isobar: W12 = p ·DV
DQ = cp · m · DT
DU = cV · m · DT
W12
p
T2
T1
W12
V1
isotherm: DU = 0
V2
K-H. Kampert ; Physik für Bauingenieure ; SS2001
V
W12
V1
V2
= m ⋅ Rs ⋅ T ⋅ ln
V1
p
= m ⋅ Rs ⋅ T ⋅ ln 1
p2
T1
V2 V
7
Adiabatische Zustandsänderung
Während der Zustandsänderung wird das Gas thermisch isoliert
fl DQ = 0
DQ = 0 = DU + DW
p
Isothermen
Adiabate
DQ
T1=const Auswertung erfordert wieder Zustandsgleichung:
=0
T2=const
DW
V1
⇒
V2 V
V2
⇔
= cv · m· DT + W12
‹ W12 = - cv · m · DT = ∫ p(V) · dV
V2
∫
V1
T
2
dV
dT
(c p − cv ) ⋅ ∫
= − cv ⋅ ∫
V
T
V1
T1
K-H. Kampert ; Physik für Bauingenieure ; SS2001
p(V) = m · R s · T / V
m ⋅ Rs ⋅ T
⋅ dV = − cv ⋅ m ⋅ dT
V
V2
T2
dV
dT
⇒ Rs ⋅ ∫
= − cv ⋅ ∫
V
T
V1
T1
⇒
(c p − cv ) ⋅ ln
V2
T
= − cv ⋅ ln 2
V1
T1
8
Adiabatische Zustandsänderung (2)
(c p − cv ) ⋅ ln
⇔
V2
T
= − cv ⋅ ln 2
V1
T1
Mithilfe der Zustandsgleichung können wir auch
T in Relation zu p, oder V in Relation zu p bringen:
p1 ⋅ V1 p2 ⋅ V2
V
p ⋅T
=
= const. ⇒ 2 = 1 2
T1
T2
V1 p2 ⋅ T1
c p − cv
V
T
⋅ ln 2 = + ln 1
cv
V1
T2
 V2 
T1
⇔
=  
T2
 V1 
c p − cv
cv
cp
 V2  cV
= 
 V1 
mit
cp
Adiabatenkoeffizient κ =
cV
dann:
 V2 
T1
= 
T2
 V1 
κ −1
❶
−1
 p1 ⋅ T2 
T1
⇒
= 

T2
p
⋅
T
 2 1
 p1 
 
 p2 
T1  p1 
⇒
= 
❶❷ ❸:
T2  p2 
Poissonsche Gleichungen
K-H. Kampert ; Physik für Bauingenieure ; SS2001
κ −1
κ −1
T 
=  2
 T1 
 p1 
= 
 p2 
−1− (κ −1)
κ −1
 T2 
⋅ 
 T1 
T 
=  2
 T1 
−κ
κ −1
 T2 
= 
 T1 
T 
=  1
 T2 
−1
κ
❶,❷ gleichsetzen:
κ −1
κ
❷
⇒
p1  V2 
= 
p2  V1 
κ
❸
9
Aus Gl ❸ findet man unmittelbar:
p1 V2κ
= κ ⇔ p1 ⋅ V1κ = p2 ⋅ V2κ = p ⋅ V κ = const
p2 V1
Poissonsches Gesetz
( Gleichung der Adiabaten
des idealen Gases )
Bsp: Dieselmotor
Berechnen Sie die Temperaturerhöhung der angesaugten Luft in einem Dieselmotor.
Es handelt sich hierbei näherungsweise um eine adiabatische Kompression von Luft
(T1 = 25°C, p1 = 1 bar, κ=1,4) von 1 bar auf 38 bar.
T1  p1 
Gleichung ❷ liefert Relation zwischen T und p:
= 
T2  p2 
 p2 
⇒ T2 = T1 ⋅  
 p1 
κ −1
κ
38 

= 298 K ⋅
 1
1.4 −1
1.4
κ −1
κ
⇔
T2  p2 
= 
T1  p1 
κ −1
κ
≅ 843 K = 570 °C
Welche mechanische Arbeit wird hierbei an dem Gas geleistet ?
K-H. Kampert ; Physik für Bauingenieure ; SS2001
10
Volumenarbeit bei adiabatischer Kompression
p
W12 = ∫ p·dV = –DQ
= - cv·m· DT < 0 ; am Gas wird
Adiabate
Arbeit
DQ
= + cv·m· (T1–T2) < 0
T2=const
=0
geleitstet
Isothermen
T1=const
W12
V2
V1 V
p1 ⋅ V1 p2 ⋅ V2
p ⋅V
=
= const. ⇒ T2 = 2 2 ⋅ T1
T1
T2
p1 ⋅ V1

 p V − p2V2 
m ⋅ cv ⋅ T1
pV 
=
W1, 2 = m ⋅ cv  T1 − 2 2 T1  = m ⋅ cv ⋅ T1  1 1
( p1V1 − p2V2 )

p1V1
p1V1 
p1V1



(
)
Benutze p1V1 = m ⋅ Rs ⋅ T1 = m ⋅ c p − cv ⋅ T1
1
m ⋅ cv ⋅ T1
⇒ W1, 2 =
( p1V1 − p2V2 ) = κ − 1 ( p1V1 − p2V2 )
m ⋅ c p − cv ⋅ T1
(
K-H. Kampert ; Physik für Bauingenieure ; SS2001
)
11
Polytrope Zustandsänderungen
Praxis: weder isotherme noch adiabatische Zustandsänderungen leicht realisierbar
(es gibt weder eine ideale Kopplung mit einem Wärmebad noch eine ideale Isolation)
Vergleicht man beide Prozesse:
p1 V2
isotherm, z.B:
=
p2 V1
Isotherm entspricht adiabatisch für k=1
κ
p1  V2 
adiabatisch:
= 
p2  V1 
Führe daher zur Beschreibung von Mischformen den
Polytropenkoeffizienten n ein, mit 1< n < k
⇒
K-H. Kampert ; Physik für Bauingenieure ; SS2001
p ⋅ V n = const
Gleichung der Polytrope
eines idealen Gases
12
Bsp: Entspannung von Druckluft
Entspanne 1 kg Druckluft ( κ = 1.4) von p1 = 10 bar auf p2 = 1 bar.
Die Anfangstemperatur T sei 20°C. Wie groß ist die Temperatur nach
dem Vorgang, wenn dieser (a) adiabatisch und (b) polytrop (n = 1.2) abläuft ?
1
= 293 K ⋅ "# $%
10
" 1$
= 293 K ⋅ # %
10
1.4−1
1 .4
1.2−1
1 .2
= 152 K = -121 °C
= 200 K = - 73 °C
Wie groß ist die mechanische Arbeit in beiden Fällen (cv = 718 J/(kg·K) )?
J
adiabatisch: W12 = m · cV (T1 T2 ) = 718 ⇥ (293 152)K = 101kJ
K
 1
J 0.4
(T1 T2 ) = 718 ·
· (293 200)K = 132 kJ
polytrop: W12 = m · cV ·
n 1
K 0.2
(Erklärung: die zusätzlichen 31 kJ werden der Umgebung als Wärme entzogen,
daher kein „Gewinn“ gegenüber dem adiabatischen Fall!)
K-H. Kampert ; Physik für Bauingenieure ; SS2001
13
Übersicht
=adiabatisch
K-H. Kampert ; Physik für Bauingenieure ; SS2001
14