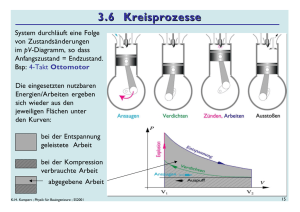
α ∆

3.2 Verhalten der Körper bei T-Änderung
Ausdehnung fester und flüssiger Körper
a) Längenausdehnung:
Die meisten Flüssigkeiten und FK dehnen sich bei Erwärmung in
alle Richtungen aus
1-dimensional:
l(T0)
l(T1)
l(T1 ) = l(T0 ) ⋅ (1 + α ⋅ ∆T )
Abkühlung: T 1 < T0 fl Dl ist negativ
(Kontraktion)
K-H. Kampert ; Physik für Bauingenieure ; SS2001
∆l 1  1 
α=
⋅
l0 ∆T  K 
Längenausdehnungskoeffizient
V: Stahl, Alu, Bolzensprenger
27
Wiederholung vom 30.4.01
Zustandsgleichung: p·V=N·k · T=n·Rm·T=m·R s·T
Mittlere Geschwindigkeit
der Gasmoleküle:
1
3
3 ⋅ kB ⋅ T
2
mN ⋅ u = ⋅ kB ⋅ T ⇔ u =
2
2
mN
Barometrische Höhenformel: ph = p0 ⋅ e
−
h
h0
∆l
Längenausdehnung:
= α ⋅ ∆T ⇔ l(T1 ) = l(T0 ) ⋅ (1 + α ⋅ ∆T )
l0
K-H. Kampert ; Physik für Bauingenieure ; SS2001
28
Tabelle: Längenausdehnungskoeffizienten
StoffMessing
a [1/K]
Aluminium
24·10-6
Messing
18·10-6
Stahl, Kupfer
(13-17)·10-6
Grauguß
9·10-6
Blei
31·10-6
Glas
(6-9)·10-6
Quarzglas
0.5·10-6
Kalkstein
4·10-6
Stahlbeton
(10-15)·10-6
K-H. Kampert ; Physik für Bauingenieure ; SS2001
29
b) Volumenausdehnung
V (T1 ) = V (T0 ) ⋅ (1 + γ ⋅ ∆T )
Volumenausdehnungskoeff.
g ≈ 3·a
Beachte:
Das gilt auch für
hohle Körper!
l1 = l0 ⋅ (1 + α ⋅ ∆T )
Erklärung:
3
3
=
l
⋅
(
1
+
α
⋅
∆
T
)
V1 ∝ l
0
3
1
á1
≅ l03 ⋅ (1 + 3α ⋅ ∆T )
= V0 ⋅ (1 + γ ⋅ ∆T )
K-H. Kampert ; Physik für Bauingenieure ; SS2001
30
Tabelle: Volumenausdehnungskoeffizienten
Stoff
g [1/K]
Quecksilber
182·10-6 (0...100 °C)
Alkohol
293·10-6 (18...39 °C)
Wasser
- 68·10-6 (0 °C)
0.0 (4 °C)
207·10-6 (20 °C)
Ausdehnung der Flüssigkeiten ist größer als
die der meisten Festkörper !
K-H. Kampert ; Physik für Bauingenieure ; SS2001
31
Anomalie des Wassers
Maximale Dichte
bei 4 °C
K-H. Kampert ; Physik für Bauingenieure ; SS2001
32
Beachte:
1) Volumenausdehnung ist automatisch mit einer
Dichteänderung verknüpft:
m
ρ0
m
=
=
ρ1 =
V0 ⋅ (1 + γ ⋅ ∆T )
1 + γ ⋅ ∆T
V1
2) Wenn sich eine Flüssigkeit im Gefäß befindet gilt:
γ scheinbar = γ Fl − γ Gefäß
c) Flächenausdehnung
A(T1 ) = A(T0 ) ⋅ (1 + β ⋅ ∆T )
Flächenausdehnungskoeff.
b ≈ 2·a
K-H. Kampert ; Physik für Bauingenieure ; SS2001
Beweis analog...
33
d) Ausdehnung von Gasen:
Gase reagieren sehr empfindlich auf T-Änderungen
Gay-Lussac fand 1802:
Gas
V (T ) = V0 ⋅ (1 + γ ⋅ ∆T )
für p=const
g (K–1)
(vgl: FK g ≈ 0.3·10-4; Fl.: g ≈ 2·10-4)
Luft
36.74·10-4
g ist nahezu gleich für alle Gase
H2
36.63·10-4
He
36.60·10-4
CO2
37.26·10-4
K-H. Kampert ; Physik für Bauingenieure ; SS2001
1
γ ≅ 36.6 ⋅ 10 [K ] =
273.2 [K]
−4
−1
34
Absolute Temperatur T:
Diese Beobachtung zeigt erneut die Existenz einer absoluten
Temperaturskala:
... für °C-Skala t :
Gay-Lussac Gesetz
V (T ) = V0 ⋅ (1 + γ ⋅ ∆T ) ⇒
g=1/273
V
V0
Vorsicht,
kein ideales
Gas !!
0
-273
1 

Vt = V0° C 1 +
t

273.2 
273.2 + t
= V0°C ⋅
273.2
T
= V0° C ⋅
273.2
mit T = 273.2 + t
absolute Temperatur in Kelvin [K]
273
0
K-H. Kampert ; Physik für Bauingenieure ; SS2001
T [K]
T [°C]
35
Thermometer
Anwendung der Volumenausdehnung
• Quecksilber-Thermometer
(-38 - 800 °C)
• Alkohol-Thermometer
(-110 - 210 °C)
Ausdehnung in einer
Glaskapillare
... im Glaskolben
• Gasdruck-Thermometer
Krümmung zweier fest
verbundener Plättchen
durch unterschiedliche
Ausdehnung
• Bimetall-Thermometer
(-50 - 400 °C)
• Thermoelement
(-200 - 400 °C;
Cu-Konstantan)
Thermospannung zwischen
zwei Metallen unterschiedlicher Temperatur
• Widerstands-Thermometer
(-250 - 1000 °C;
Platin)
T-Abhängigkeit des
elektr. Widerstands
Kap. 3.3
• ...
K-H. Kampert ; Physik für Bauingenieure ; SS2001
V: Thermometer
36