Die Ladung eines Kondensators / Die Fläche unter einer Kurve

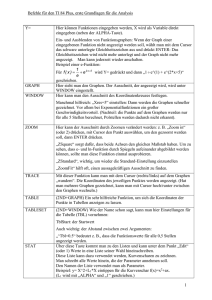
Praktikum
Die Ladung eines Kondensators
Zwei elektrisch leitende Körper, die durch
einen Isolator getrennt sind, bilden einen
Kondensator. In ihm lässt sich Ladung
­speichern.
Bauen Sie die weitere Schaltung entsprechend
dem Schaltplan und dem Foto auf. Achten Sie
auf die richtige Polung des Kondensators.
Schließen Sie den Kontakt für ca. 10 Sekunden
und messen Sie nach dem Trennen anfangs
alle 5 Sekunden die Stromstärke ¯, später alle
10 Sekunden:
Aufgabe: Bestimmen Sie die in einem
­Kondensator gespeicherte Ladung.
Geräte: Kondensator (​C​ 1​ = 1 000 µF, ​C​2​ = 3 300 µF ),
Widerstände (​R​1​ = 10 kÐ, ​R​2​ = 33 kÐ), Funktions­
generator, Messverstärker, Stromstärkemess­
gerät, Stoppuhr, elektrische Versorgung 12 V AC.
Aufbau:
t in s
0
¯ in mA …
5
10
15
20
25
30
40
…
…
…
…
…
…
…
Auswertung: Zeichnen Sie ein t-¯-Diagramm.
12 V AC
¯ in mA R
0,3 Mess­
verstärker
C = 1000 mF
R1 = 10 kÐ
0,2 C
¯
Funktions­
generator
0,1 t in s 0,0 Durchführung: Schließen Sie die Versorgungs­
spannung (12 V AC) an den Messverstärker an.
Verbinden Sie den Messverstärker über das
sechspolige Kabel mit dem Funktionsgenera­
tor. Wählen Sie am Funktionsgenerator mit
den Miniaturschaltern „Gleichspannung +“ aus.
Messen Sie die Spannung des Funktionsgene­
rators und korrigieren Sie den Wert mit dem
Amplituden-Regler auf 3 V.
0 5 10 15 20 25 30 º A1 Begründen Sie, dass die Fläche unter
dem Graphen ein Maß für die zu Beginn ge­
speicherte Ladung darstellt.
º A2 Bestimmen Sie näherungsweise die
Ladung des Kondensators aus dem Graphen.
º A3 Wiederholen Sie die Messung mit einem
Widerstand ​R​2​ = 33 kÐ.
1 Elektrisches Feld
Bildquellen: B1a, 1b Klett-Archiv, Manfred Grote
Die Fläche unter einer Kurve
Methoden
Bei einem krummlinigen Graphen kann man
die Fläche unterhalb des Graphen durch Recht­
ecke annähern ( B2 ). Die Gesamtladung er­
hält man näherungsweise durch Summenbil­
dung. Diese kann von Hand, mit einem
Tabellen­kalkulationsprogramm oder einem
GTR ausgewertet werden.
0,3 ¯ in mA
t in s
0
5
10 15 20 25 30 40 50
¯ in mA 0,30 0,26 0,22 0,19 0,16 0,14 0,12 0,09 0,07
0,2 1,3 mAs In einem t-¯-Graphen gibt eine Rechteckfläche
das Produkt aus Stromstärke und Zeit an. Zum Beispiel erhält man bei einer konstanten
Stromstärke ¯ = 0,26 mA in der Zeitspanne ð t = 5 s das Produkt ¯ · ð t = 0,26 mA · 5 s =
1,3 mAs . Dieses bezeichnet die Ladung, die in
der betrachteten Zeitspanne ð t = 5 s geflos­
sen ist.
0,1 0,0 t in s 0 5 10 15 20 25 30 35 40 45 50 B2 Entladekurve eines Kondensators
º A1 Berechnen Sie die Fläche näherungs­
weise durch Ermittlung der Rechtecksummen.
º A2 Bestimmen Sie die Fläche mit einem
Tabellenkalkulationsprogramm.
0,3 ¯ in mA
A
B
C
D
1
Zeit
¯
ð Q
Q
2
in s
in mA
in mAs
in mAs
3
0
0,3
0
0
4
5
0,26
1,3
1,3
5
10
0,22
1,1
2,4
t in s 6
15
0,19
0,95
3,35
30 7
…
…
…
…
nicht erfasste Flächen 0,2 0,1 0,0 0 5 10 15 20 25 B1 Die Fläche unter der Kurve wird durch Rechtecke
angenähert.
º A3 Ermitteln Sie die Fläche für die Recht­
ecke, die die Kurve überdecken.
Lösung mit dem GTR
Aufgabe: Geben Sie ihre Messwerte in die
Listen L1 und L2 des Taschenrechners ein:
[Stat] [1] und Ansteuern des Listenplatzes mit den Cursortasten, Eingabe mit [Enter]
abschließen.
Die Zeitspannen zwischen den Messungen
errechnet man in der Liste L3:
[Stat] [1] und Ansteuern des Spaltenkopfes der
Liste L3 mit den Cursortasten. Dann [Enter]
[2nd] [List] [OPS] [7] [2nd] [List] [1] [)] [Enter].
Nun wird in Liste L3 im ersten Feld mit [2nd]
[INS] eine 0 gesetzt, um die Liste auf die pas­
sende Länge zu bringen.
In Liste L4 sollen die Produkte aus Zeitspannen
und Stromstärken aufsummiert werden:
[Stat] [1] und Ansteuern des Spaltenkopfes der
Liste L4 mit den Cursortatsen. Dann [2nd] [List]
[OPS] [6] [2nd] [List] [2] [*] [2nd] [List] [3] [)]
[Enter].
Die Anfangsladung entnimmt man dem letz­
ten Element der Liste L4. In unserem Beispiel
sind dies 7,05 mC. Der Wert ist kleiner als der
zu erwartende Wert, da die Fläche durch die
Annäherung nicht vollständig erfasst wird.
Ein t-¯-Diagramm der Listenwerte kann über
[Graph] angezeigt werden.
Elektrisches Feld 2