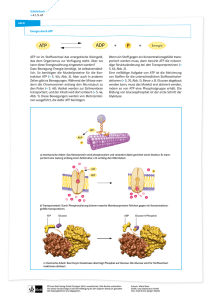
2. VL (Coenzyme, Thermodynamik)
Werbung

Vorlesung Zell- und Molekularbiologie Stoffwechsel Metabolismus (2) © H.Cypionka www.icbm.de/pmbio Coenzyme und prosthetische Gruppen © H.Cypionka www.icbm.de/pmbio 1 Coenzyme Apoenzym + Coenzym → funktionsfähiges Holoenzym • Das Coenzym kann nach der Reaktion verändert sein, das Enzym verlassen und mit einem anderen Enzym reagieren. © H.Cypionka www.icbm.de/pmbio NAD und FAD NAD FAD • sind die wichtigsten Elektronenüberträger. • NADP meist bei anabolischen, NAD in katabolischen Reaktionen • FMN ist oft fest gebundene prosthetische Gruppe von RedoxEnzymen. • Redoxpotential von NAD/NADH2: -320 mV • Redoxpotential von FAD/FADH2: ≈ -200 mV © H.Cypionka www.icbm.de/pmbio 2 Prosthetische Gruppen Prostethische Gruppen Eisen-SchwefelZentren und Porphyrine sind wichtige prosthetische Gruppen (fest gebundene Coenzyme). Porphyrine treten auch als Bestandteile von Coenzymen auf. © H.Cypionka Was sind Reduktionsequivalente? Elektronen • e- ? ← Keine freien Elektronen (Elektronenstrahl) in der Zelle! •H? ← Wasserstoffatome ?? • H+ ? ← Protonen ganz ohne Elektronen?? • H2 ? • H+ + e- ? • [H] ? www.icbm.de/pmbio ← Molekularer gasförmiger Wasserstoff?? ← Das ist gemeint, manchmal zu verwenden, siehe aber erste Zeile! ← Das ist es! • [H] beschreibt Reduktionsequivalente ohne Rücksicht auf die beteiligten Überträger. Energetische Berechnungen sind damit nicht möglich. © H.Cypionka www.icbm.de/pmbio 3 ATP ATP Anhydrid Ester Adenin N-glykosidische Bindung Nukleosid Adenosin Adenosinmonophosphat AMP Adenosindiphosphat ADP Adenosintriphosphat ATP Nukleotide © H.Cypionka www.icbm.de/pmbio Weshalb steckt in ATP Energie? ~ ~ ATP • Zahlreiche O-Atome und negative Ladungen stoßen sich ab • Oft Mg2+ zur Kompensation benötigt Wieviel Energie steckt in ATP? ATP + H2O → ADP + Pi ∆G°' = -31.8 kJ/mol (-7.6 kcal/mol) • Hydrolyse, Wasser oft nicht aufgeschrieben • ° bezeichnet Standard-Bedingungen (manchmal auch °): - alle Konzentrationen 1 mol/l, Wasser 1, Gase 1 atm - Temperatur 25 °C = 298 K • ' bedeutet [H+] = 10-7 mol/l, d.h. pH = 7 wg. Milieu biologischer Systeme • Phosphatgrupppen meist nicht abgespalten sondern übertragen © H.Cypionka www.icbm.de/pmbio 4 Wieviel Energie steckt im ATP? ATP PPi = Pyrophosphat, Abspaltung bei besonders wichtigen Reaktionen, z.B. Protein- oder DNASynthese *) ~ ~ Freie Energie ∆G0’ einiger Reaktionen von ATP kJ/mol ATP + H2O → ADP + Pi ATP + H2O → AMP + PPi*) -31.8 -41.7 ATP + AMP → 2 ADP PPi + H2O → 2 Pi 0 Achtung: Werte gelten nur unter Standardbedingungen bei pH = 7 -21.9 Die Adenylatkinase ist eines der aktivsten Enzyme: ATP + AMP ↔ 2 ADP A-R-P-P-P + P-R-A ↔ A-R-P-P + P-P-R-A © H.Cypionka www.icbm.de/pmbio Wieviel ATP ist in der Zelle? ATP Energieladungszustand (energy charge, EC) der Zelle EC = [ATP] + 0.5 [ADP] [ATP] + [ADP] + [AMP] > 0.8 z.B. [ATP] ≈ 10 mM, ADP ≈ 1 mM, AMP ≈ 1 mM EC = 10.5/12 = 0.875 D.h. die Zelle ist normalerweise immer energetisch aufgeladen. © H.Cypionka www.icbm.de/pmbio 5 Wieviel ist ATP in der Zelle wert? ATP Berücksichtigung von Konzentrationen für energetische Berechnungen: ∆G = ∆G° + RT ln(cProdukt/cEdukt) bei mehreren Edukten und/oder Produkten wird multipliziert: ∆G = ∆G°+ RT ln(CP1 . CpP2 / CE1 . CE2) • Chemiebuch (Standardbedingungen) ATP + H2O → ADP + Pi ∆G°' = -32 kJ/mol • In der Zelle: [ATP]≈0.01 M, [H2O]='1', ADP≈0.001 M, [Pi] ≈0.01 M Produkt-Edukt-Verhältnis wird (0.001*0.01)/(0.01 * 1) = 0.001 ∆Gbiol. = ∆G0' + RT ln 0.001 = ∆G0' -17 = -49 kJ/mol ∆Gbiol= -50 kJ/mol • Für Regenerierung aufgewendet: meist etwa 75 kJ/mol ATP In der Zelle ist ATP mehr wert als unter Standardbedingungen und auch nicht so leicht zu regenerieren. © H.Cypionka www.icbm.de/pmbio Mechanismen der ATP-Nutzung ATP-Nutzung Typische anabole Reaktionen sind endergon und nicht spontan ablaufend: X → Y ∆G > 0 Aber (a) X + ATP → X-Pi + ADP ∆G ≤ 0 (möglich) (b) X-Pi → Y + Pi ∆G ≤ 0 (möglich) ________________________________________________________ Summe (a + b) X + ATP → Y + ADP + Pi ∆G ≤ 0 (möglich) Reaktionsgleichungen und ∆G-Werte dürfen addiert und substrahiert werden. Für mindestens eine der Reaktionen a und b muss ∆G < 0 sein. © H.Cypionka www.icbm.de/pmbio 6 Mechanismen der ATP-Regenerierung ATP-Regenerierung Es gibt nur zwei Möglichkeiten. • Substrat-Phosphorylierung (b + a rückwärts, gekoppelt an gleichzeitige exergone Reaktionen, z.B. Redoxreaktion) • Ionentransport-Phosphorylierung (H+ oder Na+) (membrangebunden, getrieben durch elektrisches Membranpotential + chemischen Gradienten) Begriffe: Energiegewinn? 'Energie-Konservierung', 'ATP-Gewinn' ? Substratketten-Phosphorylierung, engl. substrate level phosphorylation !? Es gibt keine oxidative Phosphorylierung oder Elektronentransportgetriebene Phosphorylierung, und auch keine Photophosphorylierung Lassen Sie sich durch veraltete Begriffe nicht verdummen! © H.Cypionka www.icbm.de/pmbio Thermodynamik - Wärmelehre Haupsätze 1. Haupsatz: Die Energie eines abgeschlossenen Systems bleibt unverändert. Verschiedene Energieformen können sich ineinander umwandeln. Energieerhaltungssatz: Es gibt kein perpetuum mobile 1. Art. 2. Haupsatz: Es gibt eine extensive Zustandsgröße Entropie S, die in einem abgeschlossenen System niemals abnimmt. Es gibt kein perpetuum mobile 2. Art. 3. Haupsatz: Beim absoluten Temperatur-Nullpunkt wird die Entropie eines idealen Kristalls 0. © H.Cypionka www.icbm.de/pmbio 7 Entropie Entropie Weshalb fliegen Gasmoleküle mit ≈1000 km/h durch die Luft? Solange Teilchen bei einer Temperatur >0 K sind, enthalten sie Energie, die Entropie (Energie pro Temperatur). Diese kann (bei konstantem Druck und Temperatur) nicht für Arbeit genutzt werden. © H.Cypionka www.icbm.de/pmbio Energie/Entropie Woher weiß ich, dass die Teilchen sich nach rechts oben bewegen werden? © H.Cypionka www.icbm.de/pmbio 8 Energie/Entropie Die Wahrscheinlichkeit, dass sich Teilchen von rechts oben nach links unten bewegen, ist momentan Null. © H.Cypionka www.icbm.de/pmbio Maxwell‘s Dämon Weshalb steckt in einem Gradienten Energie? Der Dämon lässt nur heiße Teilchen von links nach rechts. Warum soll es ihne kann es ihn nicht geben können? Energie hängt ab von Information © H.Cypionka www.icbm.de/pmbio 9 Patent-Membran Weshalb steckt in einem Gradienten Energie? Die drehbaren Dreiecke lassen impulsreiche (heiße) Teilchen in eine Richtung durch. Leider verlieren die Teilchen bei der Wechselwirkung mit der Patentmembran Energie. Ohne Energie lässt sich kein Gradient herzaubern. Energie in Gradienten lässt sich aber nutzen. © H.Cypionka www.icbm.de/pmbio Energie/Entropie Wieviel Energie steckt in einem Gradienten? C2 Merken! C1 ∆G = (-)RT . ln(c1/c2) Dieselbe Formel wie bei der Berechnung der Konzentrationsabhängigkeit chemischer Reaktionen! © H.Cypionka www.icbm.de/pmbio 10 Beispiel Transportenergie: Transport Aufnahme ungeladener Teilchen über eine Membran entlang einem Gradienten caußen und cinnen seien 100 und 1 mM Es gilt (pro Mol): ∆G = -RT ln(ca/ci) ln(100) = 4.605 RT = 8.314 J mol-1 K-1 . 298 K = 2478 J mol-1 ∆G = -11.4 kJ mol-1 © H.Cypionka Chemische Energie www.icbm.de/pmbio Chemische Energie o in Reaktionsmöglichkeiten, nicht in Verbindungen! o auch Licht sofort in chemische Energie umgewandelt o Die freie Energie ∆G entscheidet, ob eine Reaktion abläuft © H.Cypionka www.icbm.de/pmbio 11 Freie Energie chemischer Reaktionen ∆G = ∆H - T . ∆S chem. Reaktionen (Gibbs-Helmholtz-Gleichung) G : freie Energie [J] (nutzbar bei T, P = const.) H : Reaktions-Enthalpie (Bestreben der Reaktanten) [J] T : absolute Temperatur [K] S : Entropie (Energie pro Temperatur, J K-1) Das ∆G chemischer Reaktionen setzt sich aus dem Bestreben zu reagieren (Enthalpie) und der Änderung der Entropie (bei Raumtemperatur meist ±10 %) zusammen. © H.Cypionka ∆G chemischer Reaktionen kann leicht aus den tabellierten Bildungsenthalpien ∆G°'(f) berechnet werden: www.icbm.de/pmbio ∆G berechnen ∆G = Σ ∆Gf(Produkte) - Σ ∆Gf(Edukte) © H.Cypionka www.icbm.de/pmbio 12 Glucose-Oxidation Beispiel Glucose-Oxidation mit Sauerstoff Dass Sauerstoff nicht direkt mit Glucose reagiert, spielt in der Thermodynamik keine Rolle, nur die Differenz zwischen Anfangs- und Endzustand. C6H12O6 + 6 O2 → 6 CO2 + 6 H2O Bildungsenthalpien ∆G°'(f) laut Tabelle unter Standardbedingungen ([°]: 25°C, je 1 mol/l in Wasser [Gas 1atm], [']: bei pH=7) in kJ/mol C6H12O6 O2 : -917.2 (Edukt: x -1) : (Edukt: x -6) 0 +917.2 0 CO2 : -394.4 (Produkt: x 6) -2366.4 H 2O : -237.2 (Produkt: x 6) -1423.2 Summe: ∆G°'= -2872.4 kJ mol-1 © H.Cypionka Energie von Redoxreaktionen ∆G = -n F . www.icbm.de/pmbio Redoxreaktionen ∆E R T ∆E = ∆E0 - n F . cred ln cox (Nernstsche Gleichung) ∆E0 : Redoxpotential unter Standardbedingungen n : Zahl der Ladungen oder Elektronen pro Reaktion F : Faradaykonstante (Energie pro mol Ladungen und Volt) 96.5 kJ mol-1 V-1 Die Faraday-Konstante erlaubt die einfache Umrechnung von ∆E und ∆G. © H.Cypionka www.icbm.de/pmbio 13 Knallgasreaktion Beispiel Knallgasreaktion H2 + ½ O 2 → H2O Standard-Redoxpotenziale 2 H+/H2 ½ O2 + 2 H+/H2O ∆G = -n F . E0' (V) -0.413 +0.814 ∆E ∆G0' = -2 . 96.5 kJ mol-1 V-1 . 1.23 V = -238 kJ/mol © H.Cypionka www.icbm.de/pmbio Knallgasreaktion Beispiel Knallgasreaktion H2 + ½ O 2 → H2O Bildungsenthalpien ∆G°'(f) laut Tabelle unter in kJ/mol Summe: H2 : 0 (Edukt: x -1) 0 O2 : 0 (Edukt: x -0.5) 0 H 2O : -238 (Produkt: x 1) -238 -238 kJ/mol © H.Cypionka www.icbm.de/pmbio 14 Lichtenergie Lichtenergie E=h.ν E : Energie in kJ/mol h : Planck'sches Wirkungsquantum (6.626 .10-34 Js) ν : Frequenz (Lichtgeschwindigkeit (≈1 sec zum Mond) [300 . 106 m/s]/Wellenlänge [nm]) Beispiel grünes Licht mit 546 nm: 220 kJ mol-1 Photonen zum Vergleich: E = m . c2 (Kernreaktionen!) © H.Cypionka www.icbm.de/pmbio 15