9 Ligandenfeldtheorie
Werbung

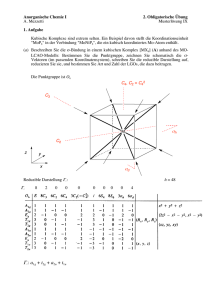
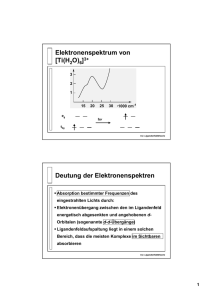
87 9 LIGANDENFELDTHEORIE 9 Ligandenfeldtheorie Qualitative MO-Theorie für einkernige Übergangsmetallkomplexe M Xm oder Übergangsmetallionen in kristallinen Festkörpern (wobei nur die nächste Koordinationssphäre mit m Anionen berücksichtigt wird. Die Niveaus der Metall(M)-Ligand(L)-Bindungsorbitale spalten infolge kovalenter und elektrostatischer Wechselwirkungen auf. Diese Aufspaltung (genauer: die Übergänge zwischen besetzten und unbesetzten Orbitalen) führt zu Signalen im optischen Spektrum solcher Systeme. Die d − d-Übergänge sind häufig im sichtbaren Bereich des Spektrums. Die qualitative Diskussion der beteiligten Orbitale erfolgt mit Hilfe der Gruppentheorie. Dazu werden nur die 4s, 4p und 3d-Orbitale des zentralen Metallatoms und die ns- und np-Valenzorbitale der Ligandenatome betrachtet. Bei mehratomigen Liganden wird dabei in der Regel nur das auf das Metall gerichtete Atom berücksichtigt. Im Folgenden wird folgende vereinfachende Schreibweise verwendet: Metallatom Liganden : : s, x, y, z, z 2 , xz, yz, x2 − y 2 , xy si , xi , yi , zi Wie bei der Konstruktion symmetrieadaptierter MOs (Abschnitt 6.3) werden nur Atomorbitale gleicher irreduzibler Darstellungen kombiniert. Zunächst werden dazu die irreduziblen Darstellungen der Ligandenorbitale bestimmt. Die irreduziblen Darstellungen der Metall-AOs lassen sich direkt aus der Charaktertafel ablesen. 9.1 Kovalente Aufspaltung Die kovalente Aufspaltung resultiert aus der Kombination von Metall-AOs und Ligandenorbitalen zu Komplexorbitalen. Bei der Konstruktion der Ligandenorbitale wird zwischen σ- und π-Bindungsorbitalen zum Zentralatom unterschieden. Zunächst werden ggf. Hybridorbitale am Ligandenatom gebildet. 88 9 LIGANDENFELDTHEORIE Beispiel 74: σ-Hybride und π-AOs im oktaedrischen Komplex ML6 Die Punktgruppe von ML6 ist Oh . Die σ-Ligandenorbitale sind spx -Hybride (vgl. Abschnitt 8). Die σ-Hybridorbitale sind auf das Zentralatom M gerichtet: z σ5 σ2 y σ3 M σ4 x σ1 σ6 σ1 σ2 = = s 1 − x1 s 2 − y2 σ3 σ4 = = s 3 + x3 s 4 + y4 σ5 σ6 = = s 5 − z5 s 6 + z6 Es wird angenommen, dass es an jedem Liganden zwei π-Ligandenorbitale gibt, wobei die Zuordnung zu π und π ′ willkürlich ist. Strenggenommen gilt dies nur für lineare Liganden wie CO, in anderen wie H2 O oder NH3 gibt es nur ein bzw. gar kein π-Ligandenorbital. Für die letzteren Systeme muss die folgende Diskussion modifiziert werden. z z π5 π5’ π2 y π3 M π4 π1 x M π4’ π6 y π2’ bzw. π3’ π 6’ π1’ x 89 9 LIGANDENFELDTHEORIE Beispiel 75: σ-Ligandenorbitale für ML6 Zur Bestimmung der irreduziblen Darstellungen der Ligandenorbitale wird zunächst das Transformationsverhalten der σ-Orbitale unter den SO der Punktgruppe Oh untersucht: C 4 ,S4 z Raumdiagonale C3,S6 L5 L2 M L3 y Mittelfläche (xy) L1 x L4 Flächendiagonale σh C2 σd L6 In der folgenden Tabelle sind nur die Ligandenorbitale angegeben, die an ortsfesten Atomen zentriert sind: E 8C3 6C2 6C4 3C42 i 6S4 8S6 3σh 6σd σ1 σ1 σ1 σ2 σ2 σ2 σ3 σ3 σ3 σ4 σ4 σ4 σ5 σ5 σ5 σ5 σ5 σ6 σ6 σ6 σ6 σ6 Γσ 6 2 2 0 0 0 0 0 4 Basis 2 ⇒ Γσ = A1g ⊕ Eg ⊕ T1u gemäß der Charaktertafel von Oh : Oh E 8C3 6C2 6C4 3C42 i 6S4 8S6 3σh 6σd A1g 1 1 1 1 1 1 1 1 1 1 x2 + y 2 + z 2 Eg 2 −1 0 0 2 2 0 −1 2 0 (2z 2 − x2 − y 2 , x2 − y 2 ) T1u 3 0 −1 1 −1 −3 −1 0 1 1 (x, y, z) Dabei transformiert die Basisfunktion 2z 2 − x2 − y 2 = 3z 2 − r2 wie z 2 . Dadurch ergeben sich folgende nichtnormierte (M+L)-Linearkombinationen für die σ-Komplexorbitale: A1g : s ± σa1g Eg T1u : : dz2 + dx2 −y2 ± σeg px + py + pz ± σt1u 90 9 LIGANDENFELDTHEORIE Beispiel 76: σ-MO-Schema für ML6 Mit den Annahmen, dass bei den meisten sn dm -Konfigurationen für die Übergangsmetall-Orbitalenergien gilt: ε3d < ε4s < ε4p , und dass die kovalente Aufspaltung der 3d-Orbitale kleiner ist als die der 4s, 4p-Orbitale, ergibt sich das folgende qualitative σ-Komplexorbitalschema: * t 1u ε a*1g 4p 4s e*g 3d t 2g Annahme: 2e − pro Ligand eg t 1u a 1g Die t2g -Metallatomorbitale dxz , dyz , dxy wechselwirken nicht mit den σ-Ligandenorbitalen. Die Elektronen des Metallatoms besetzen hier die t2g - und eg -Orbitale. Analog wird für die π-Ligandenorbitale vorgegangen: Beispiel 77: π-Ligandenorbitale für ML6 Transformationsverhalten der π-Orbitale unter den (in der Skizze aus Beispiel 75 angegebenen) SO der Punktgruppe Oh : π1 π1′ π2 π2′ π3 π3′ π4 π4′ π5 π5′ π6 π6′ Γπ E π1 π1′ π2 π2′ π3 π3′ π4 π4′ π5 π5′ π6 π6′ 12 ⇒ Γπ = T1g ⊕ T2g ⊕ T1u ⊕ T2u 6C2 6C4 3C42 0 0 π5′ −π5 π6′ −π6 0 −π5 −π5′ −π6 −π6′ −4 Oh T1g T2g T1u T2u E 3 3 3 3 8C3 8C3 0 0 0 0 6C2 −1 1 −1 1 i 0 6C4 1 −1 1 −1 6S4 8S6 3σh −π1 π1′ −π2 π2′ −π3 π3′ −π4 π4′ 6σd 0 0 0 −π5′ −π5 −π6′ −π6 0 3C42 −1 −1 −1 −1 i 3 3 −3 −3 6S4 1 1 −1 −1 8S6 0 0 0 0 3σh −1 −1 1 1 6σd −1 1 1 −1 Dadurch ergeben sich folgende nichtnormierte (M+L)-Linearkombinationen für die π-Komplexorbitale: T1g T2g : : reine Ligandenorbitale dxz + dyz + dxy ± πt2g T1u T2u : : px + py + pz ± πt1u reine Ligandenorbitale Basis (xz, yz, xy) (x, y, z) 91 9 LIGANDENFELDTHEORIE Beispiel 78: π-MO-Schema für ML6 Mit den Annahmen aus Beispiel 76 ergibt sich das folgende qualitative π-Komplexorbitalschema: * t 1u ε 4p a1g 4s t2g * 3d eg t2g M π −Ligandenorbitale t 1u Die Orbitalbesetzung hängt hier von der Anzahl π-Elektronen pro Ligand ab. Aus Übersichtlichkeitsgründen sind die nichtbindenden t1g - und t2u -Komplexorbitale aus den Ligandenorbitalen nicht dargestellt. 9.2 Elektrostatische Aufspaltung: Kristallfeld In diesem Abschnitt soll die rein abstoßende Wechselwirkung der Elektronen in den d-Orbitalen des Metalls mit den Elektronen der Liganden betrachtet werden. Im realen System (und in quantenchemischen Berechnungen) lassen sich kovalente und elektrostatische Wechselwirkungen nicht streng auseinanderhalten. Hier soll jedoch — wie in den meisten Lehrbüchern — eine solche Separation konzeptionell vollzogen werden. Zur Vereinfachung wird statt der Ladungsverteilung in den Ligandenorbitalen je eine (negative) Punktladung angenommen. Dadurch ergibt sich eine Aufspaltung der Metall-d-Orbitalniveaus unabhängig von den oben diskutierten kovalenten Orbitalwechselwirkungen. Die Coulomb-Wechselwirkung kann für jedes d-Orbital in jedem Ligandenfeld analytisch exakt berechnet werden (siehe Reinhold, S. 199 ff.). Für qualitative Betrachtungen reicht es aus, die Abstoßung aus der Orbitalform abzuschätzen. Dazu wird jeweils das Standardkoordinatensystem des Komplexes angesetzt: 92 9 LIGANDENFELDTHEORIE Beispiel 79: Qualitative Ligandenfeldaufspaltung für Oh , Td , D4h Im oktaedrischen Ligandenfeld reichen die eg -Orbitale (dz2 , dx2 −y2 näher an die Liganden heran: y dx2 −y2 e g(z 2,x 2−y2) x ∆ο y dxy t 2g (xz,yz,xy) x Oh Im tetraedrischen Ligandenfeld reichen die t2 -Orbitale (dxz , dyz , dxy ) näher an die Liganden heran. y dxy t 2 (xz,yz,xy) ∆t x y dx2 −y2 e (z 2,x 2−y2) x Td Die Aufspaltung im quadratisch pyramidalen Ligandenfeld (D4h ) hängt von den Abständen, genauer vom Höhen- zu Breitenverhältnis, ab. In jedem Fall gehört der Komplex zur Punktgruppe D4h , einer Untergruppe von Oh . Im Abschnitt 5.9 wurde gezeigt, wie die irreduziblen Darstellungen von Gruppen und Untergruppen miteinander korreliert sind. Hier spaltet die dreidimensionale Darstellung t2g (Oh ) in eg und b2g (D4h ) auf, die zweidimensionale Darstellung eg (Oh ) spaltet in a1g und b1g (D4h ) auf. eg ε t2g xz,yz,xy xz,yz b2g xy Oh 9.2.1 D4h (Verlängerung z−Achse) Jahn-Teller-Verzerrung Bei bestimmten Orbitalbesetzungen (z.B. t22g in Oh ) erfolgt durch die Aufspaltung des t2g -Orbitals bei Symmetrieerniedrigung und Umbesetzung nach dem Aufbauprinzip eine energetische Stabilisierung. Der resultierende Effekt der Strukturverzerrung wird als Jahn-Teller-Verzerrung bezeichnet. Beispielsweise bei Vergrößerung der vertikalen Ausdehnung des Oktaeders (in z-Richtung) ergibt sich folgende Reihenfolge: b1g a1g eg x 2 −y2 z2 xz,yz xy b2g 10 WOODWARD-HOFFMANN-REGELN 10 93 Woodward-Hoffmann-Regeln • Qualitative Aussage über Reaktionsbarrieren einfacher chemischer Reaktionen Anwendbar auf konzertierte Reaktionen R −→ T S −→ P (ohne Intermediate) • Unterscheidung zwischen thermisch und photochemisch aktivierten Reaktionen. • Gruppentheorie: Korrelation der Molekülorbitale von Reaktand und Produkt Die Regeln lassen sich auf zwei Arten darstellen: • Im Orbitalbild: – Die Elektronen besetzen im Reaktanden (R), im Übergangszustand (TS) und im Produkt (P) die topologisch gleichen Molekülorbitale Durch die Strukturänderungen während der Reaktion kann die energetische Reihenfolge der MOs vertauscht werden (die Klassifizierung erfolgt im einfachsten Fall nach der Knotenregel) – Eine Reaktion wird als verboten klassifiziert, wenn im Produkt höherliegende MOs besetzt sind als im Reaktanden In erlaubten Reaktionen werden im Produkt gleich hohe oder tiefer liegende MOs besetzt als im Reaktanden – Thermische Reaktionen beginnen im elektronischen Grundzustand von R, in Photoreaktionen wird im Reaktand zunächst ein Elektron in ein unbesetztes MO angeregt. • Im Zustandsbild wird gemäß der Hartree-Fock-Theorie (TC I) die Gesamtzustandsfunktion aus allen besetzten MOs betrachtet. – In thermischen Reaktionen liegt der Reaktand im Grundzustand (S0 ) vor. Gibt es während der Reaktion eine vermiedene Kreuzung mit einem doppelt angeregten Zustand gleicher Symmetrie (z.B. S2 ), besitzt die Reaktion eine Aktivierungsbarriere, sonst ist die Reaktion quasi barrierefrei, – In Photoreaktionen wird der Reaktand in den ersten angeregten Zustand (S1 ) gebracht. Die Reaktion benötigt dann eine Aktivierungsenergie, wenn eine vermiedene Kreuzung mit einem höher angeregten Zustand gleicher Symmetrie, z.B. S3 , existiert. In diesem Fall wäre eine Reaktion ausgehend vom S3 -Zustand des Reaktanden in den S1 -Zustand des Produkts quasi barrierefrei, wobei im Übergangszustand ein Übergang (Internal Conversion) S3 → S1 stattfinden müsste. Solche adiabatischen Photoreaktionen treten allerdings selten auf. 10 94 WOODWARD-HOFFMANN-REGELN Beispiel 80: Elektrocyclische Reaktionen Das einfachste Beispiel für die Anwendung der Woodward-Hoffmann-Regeln ist die Cyclisierung von s-cisDienen. h risc tato o disr kon rot ato risc h Für die Anwendung der Regeln wird das System vereinfacht und idealisiert: • Es werden nur die Atome und Atomorbitale betrachtet, die direkt an der Reaktion beteiligt sind. (hier die π-AOs der Kohlenstoffatome im Reaktanden, die sich z.T. in σ-Orbitale umwandeln) • Danach werden die Moleküle auf die Atome reduziert, an denen diese Atomorbitale zentriert sind. (hier das Kohlenstoffgerüst) • Die Strukturen werden idealisiert, d.h. es wird jeweils die höchstmögliche (sinnvolle) Punktgruppe angesetzt. (hier jeweils C2v ) Dazu werden hier die Kohlenstoffgerüste des Reaktanden und der Produkte als planar betrachtet. Die Reste R, R′ und die Wasserstoffatome werden nicht unterschieden. (für eine alternative Vorgehensweise siehe Vorlesung) In beiden Reaktionen wird eine σ-Bindung zwischen C1 und C4 und eine π-Bindung zwischen C2 und C3 gebildet, während die π-Bindungen C1 -C2 und C3 -C4 gebrochen werden. Daher sind die relevanten AOs von Reaktand und Produkt: z z π2 π3 π2 π3 y x y x π1 π4 σ4 σ1 Produkt: Reaktand: π1 = 2px,1 π2 π3 = = 2px,2 2px,3 σ1 π2 = = 2py,1 2px,2 π3 σ4 = = 2px,3 2py,4 π4 = 2px,4 Die SMOs des Reaktanden und der Produkte (die nach Idealisierung nicht mehr unterschieden werden) müssen konstruiert und nach ihrer Knotenstruktur energetisch klassifiziert werden. Danach wird versucht, eine Korrelation zwischen den SMOs herzustellen. 10 95 WOODWARD-HOFFMANN-REGELN a) Konstruktion der π-SMOs des Reaktanden Transformation der π-Orbitale in C2v C2v π1 π2 π3 π4 ΓR E Cz ✎☞ 2 π1 −π ✍✌ ✎☞ 4 π2 −π ✍✌ ✎☞ 3 π3 −π ✍✌ ✎☞ 2 π4 −π1 ✍✌ (4, σxz σyz ✎☞ π4 −π 1 ✍✌ ✎☞ π3 −π 2 ✍✌ ✎☞ π2 −π 3 ✍✌ ✎☞ π1 −π 4 ✍✌ 0, −4) = 2A2 ⊕ 2B1 0, Projektionsoperatoren PA2 : 1 (E + C2 − σxz − σyz )π1 4 1 (E + C2 − σxz − σyz )π2 4 = = 1 (π1 − π4 − π4 − (−π1 )) = 4 1 (π2 − π3 − π3 − (−π2 )) = 4 1 (π1 − π4 ) 2 1 (π2 − π3 ) 2 Die Projektionen auf π3 und π4 liefern linear abhängige Ergebnisse. PB1 : 1 (E − C2 + σxz − σyz )π1 4 1 (E − C2 + σxz − σyz )π2 4 = = 1 (π1 − (−π4 ) + π4 − (−π1 )) = 4 1 (π2 − (−π3 ) + π3 − (−π2 )) = 4 1 (π1 + π4 ) 2 1 (π2 + π3 ) 2 Die Projektionen auf π3 und π4 liefern linear abhängige Ergebnisse. Delokalisierte (nicht normierte) SMOs durch Linearkombination ψ a + = π1 + π2 − π3 − π4 2 ψ a − = π1 − π2 + π3 − π4 2 ψ b + = π1 + π2 + π3 + π4 1 ψ b − = π1 − π2 − π3 + π4 1 Klassifikation nach Knotenverhalten (Knoten in der Molekülebene werden nicht berücksichtigt) führt zum π-MO-Schema des Reaktanden: ε a2 − 3 Knoten b1 − 2 Knoten a2 + 1 Knoten b1 + 0 Knoten 10 96 WOODWARD-HOFFMANN-REGELN b) Konstruktion der σ- und π-SMOs des Produkts Transformation der σ, π-Orbitale in C2v C2v σ1 π2 π3 σ4 ΓP E Cz ✎☞ 2 σ1 −σ ✍✌ ✎☞ 4 π2 −π ✍✌ ✎☞ 3 π3 −π ✍✌ ✎☞ 2 σ4 −σ1 ✍✌ (4, 0, σxz σyz ✎☞ σ1 −σ4 ✍✌ ✎☞ π3 −π 2 ✍✌ ✎☞ π2 −π 3 ✍✌ ✎☞ σ 4 −σ1 ✍✌ 0, 0) = A1 ⊕ A2 ⊕ B1 ⊕ B2 Projektionsoperatoren 1 (E + C2 + σxz 4 1 (E + C2 + σxz 4 1 : (E + C2 − σxz 4 1 (E + C2 − σxz 4 1 : (E − C2 + σxz 4 1 (E − C2 + σxz 4 1 : (E − C2 − σxz 4 1 (E − C2 − σxz 4 PA 1 : PA 2 PB1 PB2 + σyz )σ1 = 1 (σ1 − σ4 ) 2 + σyz )π2 = 0 − σyz )σ1 = 0 − σyz )π2 = 1 (π2 − π3 ) 2 − σyz )σ1 = 0 − σyz )π2 = + σyz )σ1 = + σyz )π2 = 1 (π2 + π3 ) 2 1 (σ1 + σ4 ) 2 0 Die Projektionen auf π3 und σ4 liefern linear abhängige Ergebnisse. Klassifikation nach Knotenverhalten (die Molekülebene als Knotenebene wird hier nicht betrachtet) führt zum σ, π-MO-Schema des Produkts: Dabei wird angenommen, dass die σ-Aufspaltung stärker als die π-Aufspaltung ist. ε b2 1 Knoten (σ− antibindend) a2 1 Knoten (π− antibindend) b1 0 Knoten (π− bindend) a1 0 Knoten (σ− bindend) 10 97 WOODWARD-HOFFMANN-REGELN Eine direkte Korrelation der R- und P-SMOs ist nicht möglich: − b+ 1 , b1 (π) − a+ 2 , a2 (π) − + b1 , b1 (π) + a− 2 , a2 (π) ↔ ↔ ? ? b1 (π) a2 (π) a1 (σ) b2 (σ) Eine Zuordnung wird erst durch Betrachtung der Übergangszustände (TS) möglich. Auch die TS-Strukturen müssen idealisiert werden, um mit Symmetrieargumenten arbeiten zu können. In beiden Fällen wird das Kohlenstoffgerüst als planar angenommen, und die Reste R, R′ , H werden nicht unterschieden. Die Punktgruppen der beiden Übergangszustände unterscheiden sich: bei der disrotatorischen Reaktion bleibt die σxz -Spiegelebene erhalten (⇒ Punktgruppe Cs ), (z) bei der konrotatorischen Reaktion verbleibt die C2 -Achse aus C2v (⇒ Punktgruppe C2 ). Wie in Abschnitt 5.9 gezeigt, lassen sich durch Vergleich der Charaktere der verbleibenden SO oder der Basisfunktionen die irreduziblen Darstellungen der Reaktand- und Produktpunktgruppen mit den irreduziblen Darstellungen der TS korrelieren. Cs (σxz ) C2v C2 (z) A′ A1 A ′′ A2 A ′ B1 B ′′ B2 B A A A 10 98 WOODWARD-HOFFMANN-REGELN MO-Korrelationsdiagramme für Disrotation In den Korrelationsdiagrammen darf es keine Kreuzung zwischen Verbindungslinien gleicher irreduzibler Darstellungen geben. Die Linien müssen die tiefstmöglichen MOs gleicher irreduzibler Darstellungen verbinden. Photoreaktion Thermische Reaktion ε ε a2 a’’ b2 a2 a’’ b2 b1 a’ a2 b1 a’ a2 a2 a’’ b1 a2 a’’ b1 b1 a’ a1 b1 a’ a1 TS P R TS P R ⇒ photochemisch erlaubt ⇒ thermisch verboten MO-Korrelationsdiagramme für Konrotation Photoreaktion Thermische Reaktion ε ε a2 a b2 a2 a b2 b1 b a2 b1 b a2 a2 a b1 a2 a b1 b1 b a1 b1 b a1 TS P R TS P R ⇒ thermisch erlaubt ⇒ photochemisch verboten