Bilderbuch K12 - Fakult at f ur Physik

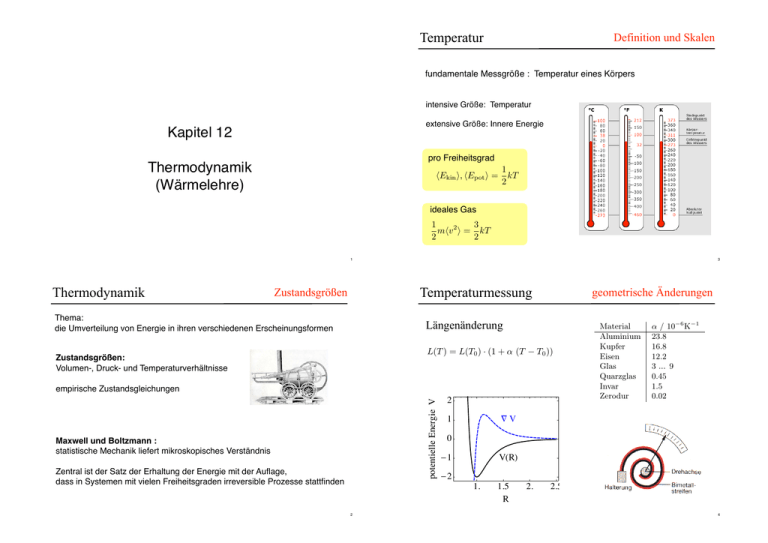
Temperatur
Definition und Skalen
fundamentale Messgröße : Temperatur eines Körpers
intensive Größe: Temperatur
extensive Größe: Innere Energie
Kapitel 12
pro Freiheitsgrad
Thermodynamik
(Wärmelehre)
hEkin i, hEpot i =
1
kT
2
ideales Gas
1
3
mhv 2 i = kT
2
2
1
Thermodynamik
3
Temperaturmessung
Zustandsgrößen
Thema:
die Umverteilung von Energie in ihren verschiedenen Erscheinungsformen
geometrische Änderungen
Längenänderung
L(T ) = L(T0 ) · (1 + ↵ (T
Zustandsgrößen:
Volumen-, Druck- und Temperaturverhältnisse
Material
Aluminium
Kupfer
Eisen
Glas
Quarzglas
Invar
Zerodur
T0 ))
Maxwell und Boltzmann :
statistische Mechanik liefert mikroskopisches Verständnis
Zentral ist der Satz der Erhaltung der Energie mit der Auflage,
dass in Systemen mit vielen Freiheitsgraden irreversible Prozesse stattfinden
2
60
—V
1
0
0
-1
-30
VHRL
-2
1.
2
30
1.5
R
2.
6
K
1
Gradient —V
potentielle Energie V
empirische Zustandsgleichungen
↵ / 10
23.8
16.8
12.2
3 ... 9
0.45
1.5
0.02
-60
2.5
4
Temperaturstabilität
Längenänderung
L(T ) = L(T0 ) · (1 + ↵ (T
Flüssigkeitsthermometer
Resonatoren
Material
Aluminium
Kupfer
Eisen
Glas
Quarzglas
Invar
Zerodur
T0 ))
↵ / 10
23.8
16.8
12.2
3 ... 9
0.45
1.5
< 0.1
6
K
geometrische Änderungen
1
L=
V
d⇡
L
V
mirrors of an interferometer
spaced by 3 Zerodur cylinders
Flüssigkeiten :
“ZERODUR®” glass ceramic
disk, 4.25 meters in diameter,
25 centimeters thick and
weighing 10 tonnes, forms
the heart of the ring laser
Hg fest bei -39 C verdampft bei 356 C (unter Druck höher)
Toluol von -80 bis +100 C
Pentan con -200 bis +30 C
SCHOTT AG Mainz
5
Temperaturmessung
(T
Gasthermometer
geometrische Änderungen
Änderung des Volumens
Änderung des Volumens bei konstantem Druck
Änderung des Volumens
V (T ) = V (T0 ) · (1 +
7
Material (20 C)
Eis (0 C)
Wasser
Quecksilber
Ethanol
T0 ))
/ 10
0.230
0.207
0.182
1.100
3
K
1
Ausdehnungskoeffizient
V
V (T ) = V (T0 ) · (1 +
V
(T
T0 ))
Änderung des Drucks bei konstantem Volumen
V (T )
=
⇡
⇡
V (T0 ) · (1 + ↵ (T
V (T0 ) · (1 + 3 ↵ (T
T0 ))
p0 V = pN k T
3
T0 )) ,
p V 0 = N k T0
p(T ) =0 p(T
0 ) · (1 +
d.h.
p
(T
Nk
(T
p0
✓
1
T0 ) = V0 · 1 +
(T
T0
V
6
3
/ 10
3.661
3.660
3.671
3.674
3.726
V
K
1
T0 ))
3↵
V = V0 +
Material (20 C)
ideale Gase
Helium
Argon
Sauersto↵
CO2
T0 )
◆
= 1/273.15 K
8
Anomalie des Wassers
Temperaturmessung
geometrische Änderungen
elektrische Änderungen
Ohmsches Gesetz
1.0000
R = R0 (1 +  (T
relative Dichte
Wasser
0.9995
T0 ))
I=
U
R
0.9990
0.9985
0.9980
-10
Eis
0.917
Ø
-5
0
5
10
15
Silizium
20
Temperatur 0 C
e
E
kT
9
Unterkühlen / Überhitzen
11
Temperaturmessung
metastabiler Zustand
Thermospannung
spontaner Phasenübergang
bei Anwesenheit eines
- Kristallisationskerns,
- Kondensationskerns
Aerosol - Wolkenbildung
elektr. Ladungen - Nebelkammer
Latentwärmespeicher
Uth = ✏ · (T1
https://www.youtube.com/watch?v=_9N-Y2CyYhM
T2 )
-35 µV/K für Pt-Konstantan
+22 µV/K for Pt-NiCr.
https://www.youtube.com/watch?v=Fot3m7kyLn4
10
12
Temperaturmessung
Temperaturmessung
über Wärmestrahlung
400
500
600
camera sensitivity
700 nm
H
Hg
diskrete Übergänge
Ne
800 nm
nahezu ein Kontinuum
Na
500 200
Na bei hohem Druck
100
energy H arb. units L
40
30
5900 K HsunL
10000
Kontinuum der Sonne
frequency H THz L
50
1000
4
Intensity H Wêm 2 L
400
100
10
1
0.1
3
integrated power
between
l = 2 and 4 mm
2
1
320 K
0.01
0
300 K
0.001
0
2
4
6
wavelength H mm L
8
260
280
300
320
Temperature H K L
10
340
13
Temperaturmessung
15
Thermisches Gleichgewicht
Plancksches Strahlungsgesetz
“green” and black body
!
Körper und Umgebung
sind bei
gleicher Temperatur
!
P( )
"
!
vacuum
"
# $ % idealer
& ' % ( ) * + # Spiegel
% , % '
wavelength
Absorptionsvermögen A = 1
w( ) =
2⇡hc2
5
exp
⇥
1
hc
kT
⇤
Die Rate mit der EM Strahlung emittiert wird
ist genau so groß wie
die Rate mit der EM Strahlung absorbiert wird.
Über 800 K ”sichtbar”
P( )
Emissionsvermögen
µm
1
P ( ) = c w( )
14
16
Gleichgewicht
Wärmebild Kameras
black-body radiation
black body radiation
PS (⌫)A(⌫) = P (⌫)AS (⌫)
Thermische Strahlung erlaubt den Austausch
von Energie zwischen 2 Körpern
ohne direkten physikalischen Kontakt.
AS (⌫) = 1
AS (⌫)
P (⌫)
A(⌫)
PS (⌫)
IR-Thermographie
Sichtbarmachung von
Wärmeverlusten in die
Umgebung
Falschfarbenbilder
Die Rate mit der EM Strahlung emittiert wird
ist genau so groß wie
die Rate mit der EM Strahlung absorbiert wird.
Die Dipole aus denen wir gebaut sind oszillieren und emittieren Strahlung
17
Emissionsvermögen
emittierte
Leistung
reflektierte
Leistung
19
INFRARED THERMOGRAPHY
black body radiation
T
absorbierte
Leistung
einfallende Leistung
jede dieser Größen ist eine Funktion der Wellenlänge
18
20
Emissivität
CCD cameras
black-body radiation
principles of operation
Ein Maß relativ
zur Emissivität
eines schwarzen Körpers
P (⌫) / E(⌫)
2-3 µm
electrons generated by internal photoeffect
are trapped between potential barriers
and are later transported away and turned into an analog signal
Leistung,
emittiert pro m2
bei der Frequenz ⌫
P (⌫), E(⌫)
CCD characteristics :
spektrale Größen
pixel number
quantum efficiency
“depth of information”
8 bit, 12 bit, 16 bit
slow, fast readout
BW or RGB
cooled / room temp.
21
heat-sinking missile & countermeasure
23
CCD cameras
Flares
principles of operation
read out
0V
scanning
HgCdTe
detector
+V
0V
500 nm
e−
10 µm
Photon
analog signal to frame grabber
22
24
Thermische Energie
Thermische Energie
Wärme und Arbeit
Der gesamte thermische Energieinhalt eines Objektes
kann nur selten präzise angegeben werden
Wärmekapazität
Spezifische Wärmekapazität:
i.A. gibt es keine einfache Beziehung zwischen
interner Energie U und Temperatur eines Objektes T
Leichter zugänglich ist die Beobachtung der
Änderung der inneren Energie.
Temperatur des
Objektes T
U = mc
Energieaustausch durch
die Oberfläche des Objektes
Experimentell beobachtet:
Beziehung zwischen Änderung
der inneren Energie ΔU und
der Temperatur eines Körpers
T
Energieaustausch durch
die Oberfläche des Objektes
U =Q+W
25
Thermische Energie
Wärme und Arbeit
Wärme:
jede Form von Energie, welche die Grenzen des
Systems (“die Oberfläche”) auf Grund einer
Temperaturdifferenz überquert
Spezifische Wärmekapazität c
c ist spezifisch für jede Substanz
c ist unterschiedlich für verschiedene Phasen einer Substanz
lineare N
Arbeit:
jede Form von Energie, die auf
Grund anderer Vorgänge in das
System oder aus dem System
gebracht werden
Energieaustausch durch
die Oberfläche des Objektes
U = mc
T
Thermische Energie
Temperatur des
Objektes T
Wärmekapazität
Thermische Energie
Thermische Energie
27
U =Q+W
Energieaustausch durch
die Oberfläche des ObjektesTemperatur
26
Steigung
dU ~ d
lineare Näherung
Temperatur
Steigung = mc
dU ~ dT
dU
dT
28
Molare Größen
Innere Energie
Avogadro
isochore Wärmekapazität
Wärmeenergie in idealen Gasen
1 mol ist diejenige Sto↵menge, die die gleiche Anzahl von Teilchen
(Atome oder Moleküle) enthält wie 12 g Kohlensto↵ des Isotops 12 C
Wkin = N · hEkin i = N f
1
kT
2
U =Nf
1
kT
2
Diese Teilchenzahl ist die Avogadro-Konstante NA
NA = 6.0221367 ⇥ 1023 mol
1
Bei V = const. gilt für die Zu- und Abfuhr von Wärme
Die Teilchenzahl in einer Sto↵menge von ⌫ mol ist N = ⌫ · NA
1 amu =
1
12
der Masse eines
Relative Atommasse Ar =
12
(1.6605 ⇥10
C Atoms
MTeilchen
1 amu
Atom
1
H
12
C
16
O
23
Na
Ar
1.007825
12.000000
15.9949
22.989767
g/mol
Molare Größen
Molvolumen eines idealen Gases
MT eilchen
1.6735
19.92648...
26.5602
38.1754
⇥10 27 kg
m
⌫
Q
⌫ CV
=
CV
=
T
und damit
isobare Wärmekapazität
System leistet Arbeit bei Vergrößerung
seines Volumens gegen äußeren Druck p
p
dV
p
bei STP*
Bei p = const. gilt für die Zu- und Abfuhr von Wärme
= NA · MTeilchen
Q
=
=
⌫ Cp
R = allgemeine Gaskonstante
R = 8.31 J /(K mol)
T
=
Cp
=
pV = ⌫ RT
=
T =C ·⌫·
oder
1
⌫f R
2
1
fR
2
Innere Energie
p Vm = NA k T = R T
Q=c·m·
T
U
31
pV = N kT
molare Wärmekapazität C
=
29
V
⌫
Vm = 22.4 dm3
molare Masse (auch Molmasse) Mm =
Für 1 Mol
isochor
kg)
Gaskonstante
molares Volumen (auch Molvolumen ) Vm =
Ideale Gasgleichung
27
T
U+
W
U +p V
oder
1
⌫f R T +p V
und damit
2
1
p V
fR+
mit pV = ⌫RT
2
⌫ T
1
f +2
fR+R=
R > CV
2
f
Cp > CV : das Gas muss Arbeit bei der Volumsausdehnung leisten
o
* STP (standard temperature and pressure) : p = 101325 Pa, T= 0 C
30
32
⌫ CV T =
Temperaturabhängigkeit
CV
1-atomig
2-atomig
3-atomig (linear)
3-atomig (nicht-linear)
=
U
nur Ekin
+ 2 Rotation
+ 1 Vibration1
+ 2 Rotation
+ 3 Vibration
+ 3 Rotation
+ 3 Vibration
molare Wärmekapazität
1
4R
oder
1
⌫f R
2
1
fR
2
T
T
T
T
T
T
T
mittel
hoch
mittel
hoch
mittel
hoch
Wärmekapazität
und
damit
Wärmekapazität
f
f
f
f
f
f
f
=3
=5
=7
=5
= 11
=5
= 12
CV = 32 R
25
CV = 72 R
CV =
11
R
2
Kupfer
20
Beryllium
15
Diamant
10
5
CV = 6 R
zählt doppelt, da kin. und pot. Energie beitragen
0
0
H2
3R
vib
2R
rot
1R
trans
0
10
Quanteneffekte
molare Wärmekapazität
=
Cv J ê K mol
Q
200
400
600
Temperatur HKL
4R
3R
vib
2R
rot
1R
trans
0
10
800
H2
50100 500 1000 5000
Temperatur HKL
Schwingungen und Rotation sind quantisiert
H2
Freiheitsgrade werden angeschaltet
wenn kT von der Größenordnung
der Schwingungsenergie ist.
50100 500 1000 5000
Temperatur HKL
http://en.wikipedia.org/wiki/File:Thermally_Agitated_Molecule.gif
33
Wärmekapazität
35
Rotationsfreiheitsgrade
Festkörper
z
Schwingungen um die Ruhelage gegenüber den nächsten Nachbarn in 3 Dimensionen:
d.h. 3 Schwingungsfreiheitsgrade, bzw. 6 Freiheitsgrade der Energiespeicherung
H2 Molekül
Radius des freien Protons ist etwa 8 × 10−16 m
niedrigste Rotationsenergiestufe
y
CV = 3 R = 24.9 J mol
1
K
1
r = 0.8 fm
x
Cv J ê K mol
25
Kupfer
20
Diamant
R = 0.1 nm
10
* Δℓ= 1 verbotener ortho-para Übergang
5
0
x ! Erot = 150 MeV
Lineare Moleküle haben keinen thermischen
Rotationsfreiheitsgrad um die Molekülachse !
Beryllium
15
y ! Erot = 15 meV *
z ! Erot = 15 meV *
Schwingungen sind quantisiert
0
200
400
600
Temperatur HKL
800
Freiheitsgrade werden angeschaltet
wenn kT von der Größenordnung
der Schwingungsenergie ist.
Trägheitsmomente der Hantel
34
{
1
mR2 = 8 ⇤ 10
2
4
Ix = mr2 = 8 ⇤ 10
5
Iy = Iz =
48
kg m2
58
kg m2
36
Ladder of rotational states
Rotation of diatomic molecules
rot
in each vibrational level
of each electronic state ....
(✓, )
`
wavefunction of the rotator
"
6
I = µ R2
moment of inertia
Hr
|L| = µ R2 !r angular momentum
Er =
rot
~2
= `(` + 1)
2µR2
5
rot
4
energy
!
3
eigenvalues
2
1
0
1 2
|L|2
I!r =
2
2µR2
Hr =
|L|2
2µR2
Hamiltonian for
the rigid rotator
rigid rotator
37
Energie in Bindungen
Rotation of diatomic molecules
H
Latente Wärmekapazität
Phasenumwandlungen brauchen Energie um
stattzufinden oder setzen Energiemengen frei
Schrödinger
equation
=E
39
eigenfunctions
Hr
rot
=
~2
= `(` + 1)
2µR2
Y`m (✓,
)
U = ± m qL
!
rot
eigenvalue
allowed values
` = 0, 1, 2, 3, . . . .
Hr =
|L|2
2µR2
Temperatur H o C L
"
rot
bei konstanter
Energiezufuhr
20
10
0
-10
-20
0
Hamiltonian for
the rigid rotator
38
100
200 300 400
Zeit HSekundenL
500
40
Wärmetransport
Wärmeleitung
3 Mechanismen
1) Konvektion
A
· (T1
l
·
Q/ t =
stationarer Fall
100
T2 )
80
A
dQ/dt
dQêdt = 10l
T2
T Ho CL
T1
l
Simulation zur Plattentektonik :
Wärmekonvektion im Erdmantel
durch viskoses Erdmantelgestein
dQ/dt =
40
20
x
konstant, weil stationär
Rayleigh-Bénard
Konvektion
Materietransport , Strömungen mit bestimmten Mustern
10
0
dQ 1
x
dt A
T (x) = const
0
0
dQ 1
dx
dt A
dT =
http://user.uni-frankfurt.de/~schmelin/what-is-convection.html
Konvektionszellenbildung
A dT /dx
60
2
4
x HcmL
6
8
10
linearer Abfall der Temperatur
41
Wärmetransport
43
Wärmeleitung
3 Mechanismen
2) Wärmeleitung
stationarer Fall
100
dT =
T1
dQ dx
dt A(x)
dQêdt = 10l
80
dQêdt = 18l
A=1
x
11
A=1
A=1+
Querschnitt A
·
A
· (T1
l
T2 )
Wärmeleitfähigkeit
x
5
T Ho CL
T2
Q/ t =
dQêdt = 4l
60
40
20
x
0
0
[ ]=
0
W
K·m
42
10
2
4
x HcmL
6
8
10
44
Wärmeleitungsgleichung
Q/ t =
·
T
A
· (T1
l
T1 T2
A
Ursachen in Flüssigkeiten
1
T2 )
✴ Keine Scherkräfte, nur
T(t)c
0.5
dQ1/dt
Wärmeleitung
zeitabhängiger Fall
dQ2/dt
Longitudinalschwellen koppeln
Nachbaratome (geringe Leitfähigkeit)
5
0.1
0.01
t=0
0
-1
x
1
-0.5
0.5
✴ In metallischen Flüssigkeiten:
1
Elektronen übertragen zusätzliche
Energie. (Hg, geschmolzene Metalle)
x
@T
@2T
=
@t
c ⇢ @x2
✴ Brownsche Bewegung erlaubt
wie die Di↵usionsgleichung
Energieübertragung
c = spezifische Wärmekapazität
⇢ = Dichte
45
Wärmeleitung
47
Wärmeleitung
Ursachen in Festkörpern
Mechanismus in Gasen
L
✴ Schwingungen einzelner Atome sind
T2
stark an Nachbaratome gekoppelt.
So gelingt der Energietransport.
T2
L⌧
x
DT
Dx
x
L
✴ In Metallen: Elektronen übertragen
zusätzliche Energie.
T1
T1
Diffusion
Wärmeleitfähigkeit ist gekoppelt mit elektrischer Leitfähigkeit
Gesetz von Wiedemann-Franz
ballistisch
𝛌 ist hier die mittlere freie Weglänge
= const · T
46
48
Wärmetransport
3) Wärmestrahlung
5.77 · 10
dW
=
dt
Stefan-Boltzmann Gesetz
8
Wm
2
K
Sichtbarkeit
4
AT4
30
1.0
25
5900 K
0.8
0.6
0.4
68 MWêm2
0.2
6â1018 m2
wHlL HWêm2 mm-1 L
wHnL H10+5 Wêm2 THz-1 L
1.2
0.0
Planck Spektrum
3 Mechanismen
200 400 600 800 1000 1200
Frequenz n HTHzL
300 K
20
15
10
460 Wêm2
5
5â1014 m2
0
2
4
6 8 10 12 14 16 18
Wellenlänge l HmmL
49
thermisches Gleichgewicht
Stefan-Boltzmann Gesetz
dW
=
dt
Absorption + Reflexion
A+R=1
P = A PS ( , T )
P = E PS ( , T )
Wärmeisolation
Wärmestrahlung
5.77 · 10
8
Wm
2
K
51
4
✴ dünn
AT4
P( )
✴ Vakuum
PS ( )
✴ verspiegelt
A
Emissionskoeffizient
Emissionsvermögen
50
52
Hauptsätze der Thermodynamik
Wärmekraftmaschine
= innere Energie + Energie die notwendig war um
dem Volumen V beim Druck p Platz zu schaffen
Enthalpie H
Energieerhaltungssatz
Energieerhaltungssatz
Wärmereservoir
Wärmereservoir
dU = dQ + dW
dU = dQ
dQ<0
System leistet Arbeit bei
Vergrößerung seines Volumens
gegen den äußeren Druck p
dQ>0
System
p, V, T, U, H, S
dW<0
p
dV
∂U
Cv =H
Lv
∂T
C p =H
∂H
Lp
∂T
dW>0
p
pdV
dQ<0
H = U + pV
System
p, V, T, U, H, S
dH
=
dU + p dV + V dp
=
dQ + V dp
Getriebe
dW =
dQ>0
dW<0
Cv =H
∂U
Lv
∂T
C p =H
∂H
Lp
∂T
dW>0
Getriebe
p dV
53
1. Hauptsatz
isochor
Energieerhaltungssatz
dH
=
dQ + V dp
pdV
dQ<0
isochore Prozesse: dV = 0
dQ
Wärmereservoir
X
Wärmereservoir
dU = dQ
isobar
X
1. Hauptsatz
55
V=const
dQ>0
System
p, V, T, U, H, S
p z p+dp
dW<0
dU = dQ = CV dT
✓
◆
@U
CV =
@T V
∂U
Cv =H
Lv
∂T
C p =H
∂H
Lp
∂T
isobare Prozesse: dp = 0
dQ
dQ<0
dQ>0
System
p=const
V z V+dV
p, V, T, U, H, S
dW>0
dW<0
Cv =H
∂U
Lv
∂T
C p =H
∂H
Lp
∂T
dW>0
dH = dQ = Cp dT
Getriebe
für
1
Mol
54
Cp =
✓
@H
@T
◆
Getriebe
p
für
ol
1M
56
1. Hauptsatz
Isothermen
für ein ideales Gas
X
Energieerhaltungssatz
dU = dQ
pdV
U=
nicht isolierter Behälter,
beweglicher Kolben
über die Systemgrenze fließt :
dQ
dU
dW
Wärme
+ Arbeit
3
T = 750K
2
isotherm:
massedichte Konzepte
isotherm
p
dT = 0
T = 250K
1
f
R T ! dU = 0
2
nicht isolierter
Behälter, starr
0
0
1
2
3
wärmeisoliert
adiabatisch
V
ZV2
dQ = p dV
Wisotherm =
p dV =
R T ln
V1
Wärme wird vollständig
in Arbeit ungewandelt.
V2
V1
ol
1M
für
dQ
dU
Wärme
dU
dW
starrer isolierter
Behälter,
Thermosflasche
Arbeit
nichts
57
1. Hauptsatz
X
317K
600K
p
458K
200K
378K
153K
dU =
Wärme fließt von selbst
immer nur vom wärmeren zum kälteren Körper,
nie in umgekehrter Richtung.
dQ=0
2
pdV
0
0
dQ = 0
1
2
3
Mechanische Arbeit kann vollständig
in Wärme umgewandelt werden.
3
2
p · V  = const
326K
126K
V
p dV = CV dT
dV
dT
R
= CV
V
T
Erfahrungstatsachen
3
1
adiabatisch:
2. Hauptsatz
adiabatisch
Energieerhaltungssatz
dU = dQ
59
1
Isotherme
dQ=0
Adiabate
T = 200K
0
0
Nur ein Teil der eingebrachten Wärme kann in
mechanische Arbeit umgewandelt werden.
T = 600K
p
1
2
3
K
V
e
zess
o
r
p
reis
 = Cp /Cv
58
60
2. Hauptsatz
Technischer Kreisprozess
Carnot Prozess (1842)
Frischluft
Abgase
http://de.wikipedia.org/wiki/Ottomotor
Ottomotor
Erste und immer noch gültige
quantitative Aussage über den Bruchteil der Wärme,
die maximal in Arbeit umgewandelt werden kann.
10
3
8
1 dQ=0
3.0
1-2 isotherme Expansion
Wärme zugeführt
dQ HzuL
2.5
2
Tk = 375K
1.5
1.0
0.6
0.8
dQ HabL
1.0
3
1.2
p
1.4
1.6
2
4
3-4 isotherme Kompression
Wärme muß abgeführt werden
Tw = 500K
4
6
2-3 adiabatische Expansion
keine Wärme zugeführt
DW
p 2.0
dQ=0
4-1 adiabatische Kompression
keine Wärme zugeführt
0-1 Ansaugen
W
1-2 Komprimieren
3-4 Expansion
0
0
2-3 Zündung
4
2
0.5
V
1
1.5
1.0
V
4-1 Ventil offen
2.0
1-0 Ausstoß
61
Wirkungsgrad
⌘=
1 dQ=0
3.0
2
Tk = 375K
1.5
1.0
0.6
0.8
dQ HabL
1.0
⌘ ! 1 wenn Tk ! 0
1.2
3
1.4
https://webspace.utexas.edu/cokerwr/www/translation.gif
Makrozustand : gemittelte Werte liegen fest, Temperatur, Druck,...
3-4 isotherme Kompression
Wärme muß abgeführt werden
Tw = 500K
4
Mikrozustände : Ort und Impuls eines jeden Teilchens liegt fest
maximal erreichbarer
Wirkungsgrad
2-3 adiabatische Expansion
keine Wärme zugeführt
DW
p 2.0
Mikrozustände
1-2 isotherme Expansion
Wärme zugeführt
dQ HzuL
2.5
Entropie
Carnot Prozess (1842)
W
Tw Tk
=
Q
Tw
63
1.6
4-1 adiabatische Kompression
keine Wärme zugeführt
U := hEi =
S :=
X
pi E i
i
k h ln(pi ) i =
k
X
pi = Wsk für Realisierung
eines Mikrozustandes
pi ln(pi )
i
Ising Modell
V
62
64
Entropie
Energie
Fähigkeit des abgeschlossenen
Systems zur Arbeitsleistung
Fähigkeit des abgeschlossenen
Systems sich zu wandeln
Beispiel: isotherme Expansion eines Gases
V1
große Energie :
große Fähigkeit zur Arbeitsleistung
kleine Entropie :
große Fähigkeit sich zu wandeln
dS =
U=
Q+
dQ
T
W
V2
Ventil
statistische Deutung
führt man Wärme dQ zu, dann
steigt die Entropie des Systems
dS =
X
Entropie
dQ
T
S
Der Grad der Unordnung steigt bei
Zufuhr von dQ bei kleiner Temperatur
stärker an als bei hoher Temperatur
=
=
=
Ising Modell
Z
Q
T
Z V1 +V2
p dV
R dV
=
T
V
V1
V1
V1 + V 2
R ln
>0
V1
V1 +V2
Entropie steigt
für
ol
1M
65
Entropie
dS =
dQ
T
67
Entropie
Beispiele für die Entropieabnahme
Beispiel: Temperaturausgleich zweier gleicher Kupferblöcke
Kristallbildung
Q1 = mcT1
} Tm = T1 + T2
Q2 = mcT2
S1 =
Z
Tm
T1
dQ
= mc
T
S2 = m c ln
S=
S1 +
Si-Einkristall aus
einer Zonenschmelze
2
Z
Tm
T1
Ta-Einkristall
dT
Tm
= m c ln
T
T1
Tm
T2
S2 = m c ln
2
Tm
>0
T1 T2
Czochralski_Process_DE.svg
Entropie steigt
Entropieabnahme auf Kosten einer Entropiezunahme der Umgebung
66
68
Entropie
Reale Gase und Flüssigkeiten Van der Waals Gleichung
Beispiele für die Entropieabnahme
Selbstorganisation
Wechselwirkung und Eigenvolumen werden berücksichtigt
⇣
p+
a ⌘
· (V
V2
b) = R T
1.0
nahzu eine Isotherme der
idealen Gasgleichung
0.8
kritischer Punkt
0.6
Binnendruck
http://www.storyal.de/weblog2009/bilder/oktober/sahara02.jpg
p
Eigenvolumen
A
0.4
0.2
biologisches Wachstum
B
A
0.0
B
0.2
0.4
Entropieabnahme auf Kosten einer
Entropiezunahme der Umgebung
0.6
320K
315K
310K
305K
300K
0.8
V
69
Entropie
71
Flüssig-Gas Gleichgewicht
offene Systeme
Phasengleichgewicht
e
Dampfdruck
Q
Q
5 DATA TABLES
kT
= Verdampfungsenergie
22
10- 2
10- 3
offene Systeme tauschen
Energie und/oder Teilchen
mit der Umgebung aus
10- 4
http://upload.wikimedia.org/wikipedia/commons/f/fd/Thermodyn._Systeme.jpg
Druck
220 b
Bedeutung der Richtung der Zeit
dS/dt > 0
TK
flüssig
fest
1b
6.1 mb
gasf.
TT
0.01 100
374
Temperatur @o CD
Vapor Pressure (torr)
10- 5
10- 6
10- 7
10- 8
10- 9
10-10
Cs fest Cs flüssig
10-11
10-12
-50
0
50
100
150
Temperature (°C)
Figure 1: Vapor pressure of cesium from the model of Eqs. (1). The vertical line indicates the melting point.
70
72
Joule-Thomson Effekt
Technischer Kreisprozess
adiabatische Expansion
Stirling Maschine
Heizung
Ideales Gas: keine Wechselwirkung
Druckmessung
Energieinhalt des Gases
hängt nicht vom Volumen ab
Reales Gas:
Energieinhalt ändert sich
bei Entspannung (Druckerniedrigung),
wenn adiabatisch und
ohne Arbeitsleistung.
U2
U 1 = p1 V 1
p1
Kühlung
p2
Wärmespeicher
adiabatisch,
keine Wirbelbildung
p2 V 2
H = U1 + p1 V1 = U2 + p2 V2 = const
dH = 0 =
dT ⇡
⇣ @H ⌘
@V
T
dV +
⇣ @H ⌘
@T
V
dT
RT b 2a
dV
+ 1)RV 2
( f2
http://en.wikipedia.org/wiki/Stirling_engine
73
Technischer Kreisprozess
75
Osmose
Wärmepumpe / Kühlschrank
Vant Hoff
Propan :
Siedepunkt 56 °C bei 20 bar
Propandampf
gibt Wärme ab
Propandampf
komprimiert
und wird heiss
Siedepunkt -25 °C bei 2 bar
p = nkT
Propandampf wird flüssig bei
Expansion durch Drossel
nk ) cR
100C in 10 m Tiefe
http://de.wikipedia.org/wiki/Wärmepumpe
Propan nimmt Wärme
auf und verdampft
⇧ = cRT
Bis zum Anfang 1990 waren die Fluorchlorkohlenwasserstoffe
(FCKW) die bevorzugten Kältemittel. Sie kondensieren bei
Raumtemperatur unter leicht handhabbarem Druck.
Sie sind nicht giftig, nicht brennbar und reagieren nicht.
http://lp.uni-goettingen.de/get/image/7221
74
76