p S - Ccp14
Werbung

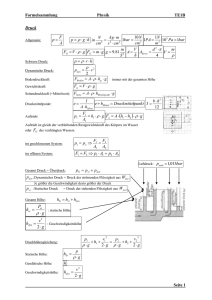
Hydro- und Aerodynamik Anwendung der BernoulliGleichung Inhalt Anwendung der Gleichung von Daniel Bernoulli bzw. des Bernoulli Effekts • Messung der Geschwindigkeit im Flug • Auftrieb an Tragflächen der Flugzeuge • Hydrodynamisches Paradoxon • Wasserstrahlpumpe Die Bernoulli-Gleichung 1 Pa Bernoulli Gleichung: Bei Erhöhung der Strömungsgeschwindigkeit fällt der Druck ab 1 Pa Druck im Bereich der höheren Geschwindigkeit v2 p2 1 Pa Druck im Bereich der kleineren Geschwindigkeit v1 v2 1 m/s Höhere Geschwindigkeit des Mediums v1 1 m/s Kleinere Geschwindigkeit des Mediums ρ 1 kg/m3 1 2 2 (v2 v1 ) p1 p2 2 p1 Dichte des strömenden Mediums Druckmessung in bewegten Objekten pS pS+D pS Druckmessungen im Fahrzeug: 1. Statischer plus dynamischer Druck pS+D im Staupunkt, („Pitot Pressure“), in diesem Punkt ruht das Medium bezüglich des Fahrzeugs, der dynamische Druck wird auch Staudruck genannt 2. Statischer Druck pS („Static Pressure“) an einer parallel zur Strömung liegenden glatten Fläche, an der das Medium ungehindert vorbeistreicht • entspricht dem barometrischen Luftdruck außerhalb des Fahrzeugs in der dem Fahrzeug entsprechenden Höhe Die Bernoulli-Gleichung für bewegte Objekte 1 Pa Bernoulli Gleichung: Bei Erhöhung der Strömungsgeschwindigkeit fällt der Druck ab 1 Pa Druck am Staurohr, “PitotDruck“, Summe aus statischem- und Staudruck pS 1 Pa Druck der vorbeiströmenden Luft, „statischer Druck“, barometrischer Luftdruck in der entsprechenden Höhe v 1m/s Geschwindigkeit des Objekts ρ 1 kg/m3 1 2 v pS D pS 2 pS+D Dichte des strömenden Mediums Nach diesem Prinzip: Druckmessung in Flugzeugen Druckmessung in Flugzeugen Staudruck = Dynamischer Druck 1 pS D pS v 2 2 dh / dt pN pN h ln g N pS Statischer + Dynamischer Druck, Pitot-Druck S D p Statischer Druck S p Luftdruck in Abhängigkeit von der Höhe über dem Meeresspiegel pS (h) p0 e 0 g h p0 ρo = 1,2928 po = 0,101325 1 kg/m3 1 MPa Dichte der Luft bei 00 C in Höhe des Meeresspiegels Luftdruck bei 00 C in Höhe des Meeresspiegels F1(h=0 m) 0,1 0,08 8000 Luftdruck Pa Luftdruck [MPa] 10000 0,06 6000 0,04 4000 0,02 2000 0 2000 4000 6000 Höhe über NN in m 8000 10000 Messung des dynamischen und statischen Drucks in einem Gerät: Das Prandtlsche Staurohr Statischer Druck pS Statischer plus Dynamischer Druck, Pitot-Druck pS+D im Staupunkt des Körpers Die Anzeige liefert den Staudruck pS+D - pS Versuch: Magnus Effekt Unterschiedliche Strömungsgeschwindigkeiten an der Oberfläche! • Druckunterschied an einem in einer Strömung rotierenden Körper • In welcher Richtung wirkt die Kraft? Versuch: Wasserstrahlpumpe • Die schnell austretenden, versprühenden Wasserteilchen reißen die Luft mit: Die Geschwindigkeit der umgebenden Luft steigt, der Druck fällt Versuch: Schwebender Ball • Ausströmende Luft hält einen Ball in einiger Entfernung vom Auslass tanzend in der Schwebe Versuch: Hydrodynamisches Paradoxon • Eine entgegen der Strömung auf den Auslass gedrückte Platte wird angezogen, schwebt auf einem Luftkissen und lässt sich nur mit Kraft abziehen: „Hydrodynamisches Paradoxon“ • Begründung: Im Bereich hoher Strömungsgeschwindigkeit, zwischen Platte und Rand des Auslasses, fällt der Druck stark ab • So entsteht das knatternde Geräusch bei Strömungen an flexiblen Auslässen (z. B. Luftablass aus einem Luftballon): Der Unterdruck im Auslass schließt, die Strömung bricht ab, elastische Rückstellkräfte öffnen wieder usw. Auftrieb am Flügel • Durch die Form des Flügels ergibt sich ein größerer Weg und deshalb eine höhere Geschwindigkeit an seiner Oberseite • Höherer Druck an der Unterseite Auftrieb Auftrieb und Widerstand bei Vereisung einer Tragfläche (FAZ 21.12.99, S. T 2) Der Limulus darf bei Strömung nicht abheben - bauen „Eiszapfen“ ähnliche Strukturen auf seinem Rücken den Auftrieb ab? (Bildquelle: Meyers Enzyklopädisches Lexikon) Wirkung von Turbulenzen Voraussetzung des Bernoulli Effekts ist eine nicht turbulente Strömung • Bei entsprechender Veränderung der Flügelform entstehen Turbulenzen, sie verkleinern den Auftrieb bis auf Null • Anwendung – Störklappen („Spoiler“) am Flugzeug, unmittelbar vor dem Aufsetzen auf die Landebahn schnell ausgefahren, „verderben“ das Flügelprofil und schalten dadurch den Auftrieb aus – „Spoiler“ an sehr schnell fahrenden Autos, um den durch das Flügelprofil der Karosserie (die Unterseite ist eben, die Oberseite gewölbt) erzeugten Auftrieb auszuschalten und die Haftung auf der Straße zu erhalten Zusammenfassung Anwendung des Druckunterschieds in Strömung mit unterschiedlicher Geschwindigkeit: • Geschwindigkeitsmessung mit Hilfe von zwei Druck Messungen im Staupunkt pS+D („Pitot Druck“) und im vorbeiströmenden Medium pS („Statischer Druck“) – ρ·v2 / 2 = pS+D + pS [Pa] – ρ [kg/m3] Dichte des Mediums – v [m/s] Geschwindigkeit des bewegten Objekts bezüglich des Mediums • Hydrodynamisches Paradoxon – Folge: Knatterndes Geräusch bei Strömungen an flexiblen Auslässen (z. B. Luftablass aus einem Luftballon) • • Auftrieb am Flügel-Profil Aber: Turbulenzen am Flügel verkleinern den Auftrieb bis auf Null – Anwendung: Störklappen („Spoiler“) am Flugzeug, die zum Aufsetzen auf die Landebahn den Auftrieb ausschalten • (http://www.grc.nasa.gov/WWW/K-12/airplane/spoil.html) – „Spoiler“ an Rennautos, um Straßen-Kontakt mindernden Auftrieb auszuschalten • • • Flüssigkeits-Zerstäuber Wasserstrahlpumpen Beim Husten zieht der Unterdruck in der Strömung störende Objekte aus den Atemwegen finis So fliegen die Vögel! …und die Flugzeuge