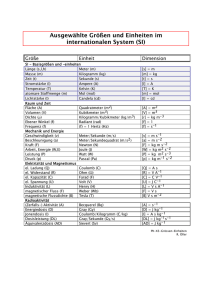
0b. Math+SI Einheiten
Werbung

Physik Ulrich Haas: Physik für Pharmazeuten und Mediziner Ein Lehrbuch für Studierende mit Physik als Nebenfach Wissenschaftliche Verlagsgesellschaft mbH Stuttgart 2002 6. Auflage ISBN 3-8047-1823-X Vorbereitungs Jahrgang 2010-11. Gruppe 2. Thematik Wichtigkeit der Lösung der Aufgaben! Ich schlage Ihnen vor sich mit den Problemen (Aufgaben) richtig zu beschäftigen. Mathematische Grundlagen Physikalische Gröben, Einheiten Mechanik Kinematik (Bewegungen) Dynamik (Lehre der Kräfte) Arbeit – Energie – Leistung Feste (starre) Körper; Impuls – Dehimpuls Deformierbare feste Körper (Elastizitätslehre) Ruhende Flüssigkeiten und Gase (Hydro- und Aerostatik) Grenzflächeneffekte Bewegte Flüssigkeiten und Gase (Hydro- und Aerodynamik) Wärmelehre (Thermostatik und Thermodynamik) Grundbegriffe – Temperaturskalen – Temperaturmessung Thermische Eigenschaften von Festkörper, Flüssigkeiten und Gasen Kinetische Wärme- und Gastheorie Wärme als Energie Aggregatzustände der Materie Wärmeübertragung - Diffusion Eigenschaften von Lösungen, Reaktionskinetik Elektrizität und Magnetismus Elektrostatik – Elektrisches Potential (elektrische Spannung) – Kapazität Stationäre elektrische Strom – Kirchhoff’sche Regeln Ladungstransport in Materie und Vakuum Elektromagnetismus – Induktion Wechselstrom Messung elektrischer Ströme und Spannungen Dielektrische und magnetische Eigenschaften der Materie Schwingungen und Wellen Mechanische Schwingungen Mechanische Wellen Schallwellen - Akustik Elektromagnetische Wellen Optik Allgemeine Eigenschaften des Lichtes Geometrische Optik Physikalische Optik Atomische Struktur der Materie Atome – Wellen- und quantenmechanische Atommodell Moleküle – Bindungen – Festkörper Radioaktivität Strahlung Quellen Gröβen Spektren Wirkungen – Nachweis – Dosimetrie Mathematische Grundlagen Begriffe und Formeln aus Arithmetik und Algebra Potenzen und Wurzeln am = a·a·a·...·a (m Faktoren) a: Basis m: Exponent Ist der Exponen ein Bruch: m/n , so stellt die Potenz am/n eine Wurzel dar. Rechenregeln: am+n = am·an usw. Logarithmen Der Logarithmus der Zahl b zur Basis a ist eine Zahl m und schreibt man: m = loga b, dabei gilt, dass m diejenige Hochzahl ist, mit der man die Basis a potenzieren muss, um die Zahl b zu erhalten: b = am. Rechenregeln (unabhängig von der Basis): log(b·c) = log b + log c usw. Mathematische Grundlagen Gleichungen mit einer Unbekannten Lineare Gleichung: a·x + b = 0. Lösung: x = -b/a. Quadratische Gleichung: a·x2 + b ·x + c = 0 besitzt zwei Lösungen x1 und x2 x1, 2 b b 4ac 2a 2 reel und verschiede n, wenn reel und gleich, wenn b 2 4ac 0, b 2 4ac 0, konjugiert komplex, wenn b 2 4ac 0. Formeln der Geometrie und Trigonometrie Rechtwinkliges Dreieck Fläche: A =1/2·a·b (a, b: Katheten) c Satz des Pythagoras: c2 = a2 + b2 (c: Hypotenuse) a Einfache trigonometrische Funktionen: sin α = a/c Gegenkathete / Hypotenuse cos α = b/c Ankathete / Hypotenuse α b Mathematische Grundlagen tan α = a/b Gegenkathete / Ankathete cot α = b/a Ankathete / Gegenkathete Wichtige Beziehungen sin2α + cos2α = 1 tan α = sin α/cos α = 1/cot α sin(α+β) = sin α·cos β + cos α·sin β usw. y Rotierende Einheitsvektor sin α 1 α cos α x Mathematische Grundlagen Allgemeines Dreieck; Fläche: 1/2·a·b·sin γ Winkelsumme: α+β+γ=180o Sinussatz: a/sinα = b/sinβ = c/sinγ a2 = b2 + c2 -2bc·cosα Cosinussatz: b2 = a2 + c2 -2ac·cosβ c2 = a2 + b2 -2ab·cosγ Gleichseitiges Dreieck; Fläche, Höhe Rechteck; Diagonale, Fläche Parallelogram; Fläche, Höhe Kreis; Umfang, Fläche, Kreisbogen: r·α(rad); Bogenmaβ des Winkels α Ellipse F b e 0 F e a F: Brennpunkt; 0: Mittelpunkt Fläche: π·a·b Lineare Excentrizität: e2 = a2 – b2 Numerische Excentrizität: ε =e/a Mathematische Grundlagen Quader; Kantenlängen a, b, c Raumdiagonale, Oberfläche, Volumen Würfel; Kantenlänge: a Raumdiagonale, Flächendiagonale, Oberfläche, Volumen Kugel; Radius: r Volumen, Oberfläche Zylinder; Gerader (senkrechter) Kreiszylinder Mantelfläche, Oberfläche, Volumen Kreiskegel; Gerader Kreiskegel Mantelfläche, Oberfläche, Volumen Funktionen und ihre graphische Darstellung Beispiele einfacher Funktionen Gerade; lineare Funktion: y = a·x + b Potenzfunktion: y = a·xn Kreis und x x0 2 y y0 2 r 2 Ellipse x x0 2 y y 0 2 a 2 b 2 1 Mathematische Grundlagen Hyperbel: x·y = a Exponentialfunktion: y = b·acx , y = b·ex , Euler’sche Zahl Logarithmusfunktion: y = logax , y = ln x Sinus- und Cosinusfunktion: y = r·sin x, (x im Bogenmaβ) Vektoren Skalare Gröβe: durch den Betrag eindeutig festgelegt. Vektor: zwei Angaben sind erforderlich: Betrag und Richtung Einheitsvektor: der Betrag ist 1. Grundoperationen der Vektoralgebra Addition von Vektoren Subtraktion von Vektoren Zerlegung in Vektorkomponenten in kartesischen Koordinaten Mathematische Grundlagen Multiplikation von Vektoren 1. die Multiplikation eines Vektors mit einem Skalar (einer Zahl); als Resultat ein Vektor, BkA 2. die Multiplikation von zwei Vektoren, dem Skalarprodukt; als Resultat ein Skalar, A B A B cos A, B Ax B x Ay B y Az B z 3. die Multiplikation von zwei Vektoren, dem Vektorprodukt; als Resultat ein Vektor. C A x B (gesprochen A kreuz B) B C = AxB φ A C A x B A B sin A, B Betrag Merkregel: Korkenzieherregel (Rechtsdrehung) Schraube mit Rechtsgewinde Physikalische Gröβen – Einheiten Mengenbegriffe Einheit – Mabzahl – Dimension Internationales Einheitensytem (SI) Definitionen der SI-Basiseinheiten Vorsilben zur Bezeichnung von dezimalen Vielfachen und Teilen Abgeleitete SI-Einheiten mit besonderem Namen Mengenbegriffe – Bezogene Grössen Aufgaben Einheit – Maβzahl – Dimension Physikalische Gröβe = Zahlenwert x Einheit Die Dimension ist die Beschreibung der physikalischen Gröβe in ihren Basisgröβen (ohne Einheit). Differenz zwischen Dimension und Einheit. Geschwindigkeit: Länge/Zeit (Dimension) Meter/Sekunde (m/s) (Einheit) Internationales Einheitensytem (SI) Sieben Basisgröβen Basisgröβe SI-Einheit Abkürzung Länge Meter m Masse Kilogramm kg Zeit Sekunde s Elektrische Stromstärke Temperature Ampere A Kelvin K Stoffmenge Mol mol Lichtstärke Candela cd Definitionen der SI-Basiseinheiten Meter (m): Das Meter ist die Länge der Strecke, die Licht im Vakuum während des Intervalls von 1/299 792 458 s durchläuft. Kilogramm (kg): Ein Kilogramm ist durch die Masse eines internationalen Prototyps gegeben. Die Masse eines Zylinders der aus einer chemisch und physikalisch resistenten Platin-IridiumLegierung angefertigt ist und unter festgelegten Bedingungen in Sevres bei Paris aufbewahrt wird (seit 1889). Sekunde (s): Atomarer Zeitstandard (1967): Eine Sekunde ist das 9 192 631 770 -fache der Periodendauer eines Strahlungübergangs von Atomen des Nuklids 133Cs (Übergang zwischen den beiden Hyperfeinstrukturniveaus im Grundzustand). Kelvin (K): Das Kelvin ist das 1/273,16 -fache der thermodynamischen Temperatur des Tripelpunktes von Wasser. Definitionen der SI-Basiseinheiten Ampere (A): Das Ampere ist die Stärke eines zeitlich konstanten elektrischen Stromes, der, durch zwei im Abstand von 1 Meter angeordnete parallele Leiter fliessend, zwischen diesen eine Kraft erzeugt, die pro Meter Leiterlänge 2·10-7 N beträgt. Mol (mol): Das Mol ist die Stoffmenge eines Systems, welches so viele Einzelteilchen enthält, wie Atome in 0,012 kg des Kohlenstoffnuklids 12C enthalten sind. Candela (cd): Die Candela ist die Lichtstärke einer Strahlungsquelle, welche monochromatische Strahlung der Frequenz 540·1012 Hertz in eine bestimmte Richtung aussendet, in der die Strahlstärke 1/683 Watt durch Steradiant beträgt. Vorsilben zur Bezeichnung von dezimalen Vielfachen und Teilen Bezeichnung Internationales Kurzzeichen Zehnerpotenz Yocto Y -24 Zepto Z -21 Atto a -18 Femto f -15 Piko p -12 Nano n -9 Mikro μ -6 Milli m -3 Zenti c -2 Dezi d -1 Deka da +1 Hekto h +2 Kilo k +3 Mega M +6 Giga G +9 Tera T +12 Peta P +15 Exa E +18 Zetta Z +21 Yotta Y +24 Abgeleitete SI-Einheiten mit besonderem Namen Gröβe Name und Einheitenzeichen Basiseinheiten Andere SI-Einheiten Ebener Winkel Radiant (rad) m·m-1 Raumwinkel Steradiant (sr) m2·m-2 Frequenz Hertz (Hz) s-1 Kraft Newton (N) m·kg·s-2 J/m Druck Pascal (Pa) m-1·kg·s-2 N/m2 Energie, Arbeit, Wärmemenge Joule (J) m2·kg·s-2 N·m Leistung, Energiestrom Watt (W) m2·kgvitä·s-3 J/s Elektrische Ladung, Elektrizitätsmenge Coulomb (C) s·A A·s Elektrisches Potential, elektrische Spannung Volt (V) m2·kg·s-3·A-1 W/A Elektrische Kapazität Farad (F) m-2·kg-1·s4·A2 C/V Elektrischer Widerstand Ohm (Ω) m2·kg·s-3·A-2 V/A Elektrischer Leitwert Siemens (S) m-2·kg-1·s3·A2 A/V Magnetischer Fluss Weber (Wb) m2·kg·s-2·A-1 V·s Magnetische Flussdischte, Induktion Tesla (T) kg·s-2·A-1 Wb/m2 Induktivität Henry (H) m2·kg·s-2·A-2 Wb/A Lichtstrom Lumen (lm) cd·sr Beleuchtungsstärke Lux (lx) m-2·cd·sr Aktivität (radioaktive) Becquerel (Bq) s-1 Energiedosis Gray (Gy) m2·s-2 J/kg Äquivalentdosis Sievert (Sv) m2·s-2 J/kg Mengenbegriffe Bezogene Grössen Mengenbegriffe: allgemeine und individuelle Einheiten der Menge (Masse) Masse: m (kg) Stoffmenge: n = N/NA (mol) Avogadro-Konstante NA = 6·1023 mol-1 ist die Anzahl der Teilchen in einem Mol Substanz, Teilchenanzahl: N dimensionslos Bezogene Grössen Volumen: V (m3) Dichte: ρ = m/V ; Masse durch Volumen (kg/m3) absolute Dichte und relative Dichte Teilchenzahldichte: ρN = N/V (m-3) Konzentration: c = n/V (mol Substanz / m3 Lösung) mol/L: häufig verwendete Bezeichnung Molarität (und Einheit) für die Stoffmengenkonzentration Aufgaben 1. Was versteht man unter einer physikalischen Gröβe? 2. Welche Basisgrössen verwendet das „Internationale Einheitensystem SI”? 3. Was versteht man unter einer vektoriellen und was unter einer skalaren Grösse? 4. Geben Sie die Einheit der Länge, der Masse und der Zeit im SI an! Wie werden diese Einheiten festgelegt? 5. Wie lautet die Definition der SI-Einheit mol? 6. Welche a) dezimale Vielfache und b) dezimale Teile gibt es im SI? Wie werden sie benannt und wie lauten ihre Vorsatzzeichen? 7. Wie wird die Dichte definiert und wie lautet ihre SI-Einheit? 8. Was versteht man unter der Avogadro-Konstante und welchen Zahlenwert (mit Einheit) hat diese? 9. Wie is die Stoffenmengekonzentration definiert und wie lautet ihre Einheit?