Vom elektrischen Feld über die Relativitätstheorie zum Magnetfeld
Werbung
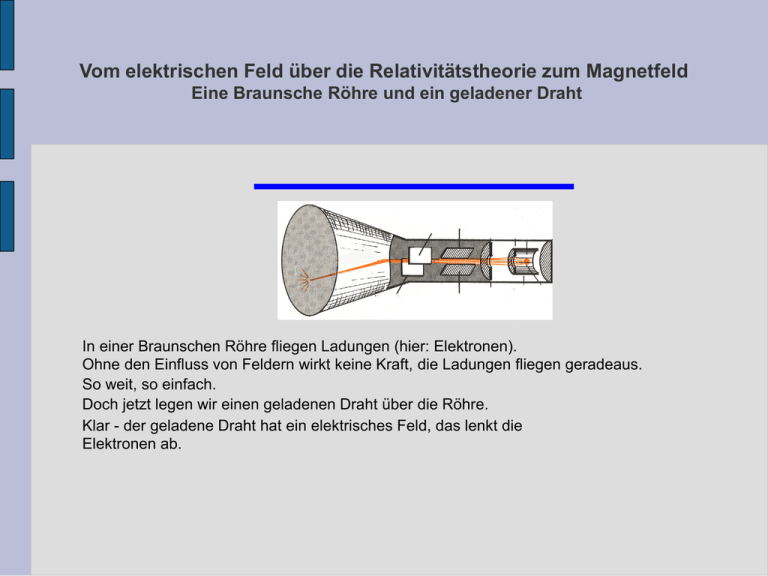
Vom elektrischen Feld über die Relativitätstheorie zum Magnetfeld Eine Braunsche Röhre und ein geladener Draht In einer Braunschen Röhre fliegen Ladungen (hier: Elektronen). Ohne den Einfluss von Feldern wirkt keine Kraft, die Ladungen fliegen geradeaus. So weit, so einfach. Doch jetzt legen wir einen geladenen Draht über die Röhre. Klar - der geladene Draht hat ein elektrisches Feld, das lenkt die Elektronen ab. Vom elektrischen Feld über die Relativitätstheorie zum Magnetfeld Jetzt lassen wir einen Strom fließen Jetzt haben wir den Draht wieder entladen, die Ladungen in der Röhre fliegen wieder geradeaus. Auch wenn wir einen Strom durch den Draht fließen lassen, ändert sich an der Gesamtzahl der Ladungen im Draht nichts - er bleibt neutral! Die Ladungen in der Röhre müssten weiter geradeaus fliegen. Tun sie aber nicht - sie werden wieder abgelenkt. Wir erklären das durch die Lorentz-Kraft, die im Magnetfeld des stromdurchflossenen Drahtes auf die bewegten Ladungen wirkt. Im Folgenden soll gezeigt werden, dass diese Kraft nichts anderes als das gemeinsame Kind von Relativitätstheorie und elektrischem Feld ist. Vom elektrischen Feld über die Relativitätstheorie zum Magnetfeld Sehen wir uns das doch mal genauer an! Eine Ladung Q fliegt mit v1 parallel zu einem stromdurchflossenen Draht (entgegen der Elektronenbewegung). Die Elektronen fließen mit der Driftgeschwindigkeit v2 im Draht. Die positiven Ladungen ruhen. Vom elektrischen Feld über die Relativitätstheorie zum Magnetfeld Eigentlich dürfte nichts passieren! Vom elektrischen Feld über die Relativitätstheorie zum Magnetfeld Und wenn wir uns mit der Ladung bewegen? Q Vom elektrischen Feld über die Relativitätstheorie zum Magnetfeld Die Auswirkung der Lorentz-Kontraktion Der Abstand der positiven und der negativen Ladungen wird durch die Lorentz-Kontraktion verkürzt, dadurch erhöhen sich die Ladungsdichten: Vom elektrischen Feld über die Relativitätstheorie zum Magnetfeld Die Auswirkung der Lorentz-Kontraktion Die Feldstärke ist jetzt nicht mehr sondern Das sieht schlimm aus, aber die Mathematik kann helfen! Vom elektrischen Feld über die Relativitätstheorie zum Magnetfeld Eine Hilfe aus der Mathe-Formelsammlung Es gibt nämlich für kleine Werte von x folgende Näherungsformel: bzw. In unserem Fall ist n = -1/2. Damit lautet die Näherungsformel Dem x entspricht natürlich v2/c2 - und das ist hier wirklich sehr klein! Vom elektrischen Feld über die Relativitätstheorie zum Magnetfeld Jetzt wird unsere Formel einfacher Damit wird unsere Formel Die binomische Formel in der Klammer müssen wir ausmultiplizieren, dann können wir weiter zusammenfassen (auf einem Zettel selber machen!). v2 (die Driftgeschwindigkei der Elektronen im Draht) ist klein, v22 erst recht. Das können wir beim Zusammenfassen getrost vernachlässigen. Dann bleibt Vom elektrischen Feld über die Relativitätstheorie zum Magnetfeld Die Kraft lässt sich jetzt berechnen Nun ist aber Damit ergibt sich für die Kraft (dem Betrage nach) Vom elektrischen Feld über die Relativitätstheorie zum Magnetfeld Wir sind am Ziel! Dies entspricht der Formel für die Lorentz-Kraft, wenn die magnetische Flussdichte eines stromdurchflossenen Drahtes ist In der Formelsammlung steht aber etwas anderes!? Wie man's nimmt - rechne mal den Wert des ersten Bruchs mit den Naturkonstanten aus und vergleiche ihn mit dem Wert der Konstanten in der Formelsammlung... Na also!











