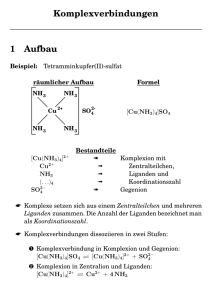
Elektrische Ladung des Komplexes
Werbung

Ligandensubstitution in oktaedrischen Komplexen: 7 Beweise für den dissoziativen Mechanismus: 1. Elektronische Gründe 2. Einfluss der eintretenden Gruppe auf die Reaktionsgeschwindigkeit (gering!) 3. Einfluss der austretenden Gruppe auf die Reaktionsgeschwindigkeit (groß!) 4. Zusammenhang zwischen Gleichgewichtskonstante und Geschwindigkeitskonstante 5. Einfluss der Ladung des Komplexes 6. Größe der Liganden 7. Aktivierungsparameter Elektrische Ladung des Komplexes • Wenn ein Anion von einem positiv geladenen Komplex abdissoziiert, und die Dissoziation der geschwindigkeitsbestimmende Schritt ist (dissoziativer Mechanismus) so sinkt die Reaktionsgeschwindigkeit mit steigender positiver Ladung des Komplexes. (Wäre der Mechanismus assoziativ, so würde der Komplex mit höherer positiver Ladung den eintretenden Liganden z.B. das polare H2O Molekül oder einen negativ geladenen Liganden, verstärkt anziehen, und die Reaktion würde mit steigender positiver Ladung des Komplexes schneller werden .) Größe des Liganden • Beispiel: methyl-substituierte Ethylendiamin Liganden • Da Methylgruppen nur einen sehr geringen induktiven Effekt haben, ist der elektronische Unterschied zwischen diesen Liganden gering • Ihre Größe steigt jedoch stark mit steigender Anzahl der Methylgruppen • Größeres Ligandenvolumen macht es leichter, eine abdissoziierende Gruppe hinauszudrängen • Steigende Reaktionsgeschwindigkeit mit steigendem Liganden-Volumen weist auf einen dissoziativen Mechanismus hin • Wäre der Mechanismus assoziativ, so würde steigendes Ligandenvolumen die Reaktion verlangsamen Aktivierungsparameter ΔS* und ΔV* • Sind bei Ligandensubstitution an oktaedrischen Komplexen meist positiv • Dies weist auf einen dissoziativen Mechanismus hin! Co3+ und die meisten anderen okteadrischen Komplexe tauschen ihre Liganden mit einem dissoziativen Mechanismus aus Ausnahmen: Die Wasser-Austauschreaktionen von Cr(H2O)63+ und von Fe(H2O)63+ zeigen ein negatives ΔV* (Ia Mechanismus) Weitere Ausnahme: Großes Zentralmetall RhNH H O 3 3 5 2 X RhNH3 5 X H 2O 2 Die RG hängt davon ab, ob X Chlorid oder Bromid ist (mit Bromid doppelt so schnell) assoziativer Mechanismus Mechanismus der basischen Hydrolyse • Unterscheidet sich stark von dem der sauren Hydrolyse • Co3+ Komplexe mit NH3 oder Aminen als Liganden hydrolysieren oberhalb pH=4 wesentlich rascher als in sauren Lösungen • Das Geschwindigkeitsgesetz ist immer 2. Ordnung: v k2 CoNH 3 5 Cl OH 2 • Würde auf einen assoziativen Mechanismus hinweisen, dies ist aber nicht der Fall! Beweis für einen dissoziativen Mechanismus: Sterischer Effekt Je größer der Amin-Ligand, desto rascher die Reaktion. Wieso kann ein dissoziativer Mechanismus zu einem Geschwindigkeitsgesetz 2. Ordnung führen? • Der NH3 Ligand wird dadurch, dass er an Co3+ koordiniert ist, fähiger, ein H+ abzuspalten • In wässr. Lsg ist das OH- -Ion nicht imstande, NH3 zum NH2- Ion zu deprotonieren. Ist aber das NH3 Molekül an das Co3+ koordiniert, so zieht das positiv geladene Metallion Elektronendichte vom NH3 ab, sodass es saurer wird • Dies ist sehr oft die Art Änderung der Liganden-Reaktivität, die in Übergangsmetall-Katalysatoren und Metalloenzymen wirksam ist. Stereochemie der oktaedrischen Substitution • Die normale oktaedrische Substitution erfolgt unter Retention der Konfiguration • Dies deutet darauf hin, dass die normale fünffach koordinierte Zwischenverbindung eine tetragonal pyramidale Struktur beibehält (quadratische Pyramide) • In manchen Fällen ist der Substitutionsvorgang jedoch von einer stereochemischen Umwandlung begleitet, z.B. • trans-[Co(NH3)4Cl2]+ + H2O ergibt 55% cis- und 45% trans-Produkt • trans-[Co(en)2(OH)Cl]+ + H2O ergibt 75% cis und 25% trans-Produkt • trans-[Co(en)2Br2]+ + H2O ergibt 30% cis und 70% trans-Produkt • Das Auftreten stereochemischer Umlagerungen kann durch die Annahme einer trigonal-bipyramidalen Struktur der fünffach koordinierten Zwischenverbindungen erklärt werden. • Der Austritt von X wird durch die Bewegung eines Paares ursprünglich trans zueinander stehender Liganden begleitet, von denen jeder cis zur austretenden Gruppe X steht • Es gibt 2 Möglichkeiten zur Bildung einer trigonalen Bipyramide • Die eintretende Gruppe Y tritt entlang einer der trigonalen Kanten ein • 6 mögliche Reaktionswege, 2 davon führen zur Wiederherstellung der relativen Positionen der Liganden im Komplex Welche Liganden ermöglichen stereochemische Umwandlung? • Voraussetzung ist das Vorhandensein eines einsamen Elektronenpaares in einem Orbital, dessen Symmetrie eine πBindung vom Liganden zum Metall ermöglicht, sobald das Umklappen von der quadratischen Pyramide zur trigonalen Bipyramide erfolgt ist: • Stabilisierung des trigonalen ÜZ Ligandensubstitution in quadratisch-planaren Komplexen • Modellfall: d8 Pt2+ Komplexe („inert“: reagieren langsam) • [Pt(dien)X]+ • X• dien Halogenidion Diethylentriamin Kinetische Studien an quadratischplanaren Pt2+ Komplexen ergeben gewöhnlich ein aus zwei Termen bestehendes Geschwindigkeitsgesetz: v k1 L3 PtD k2 L3 PtD E 2 simultane Mechanismen • Wir definieren k = k1 + k2 [E] • In einem Diagramm k gegen [E] auftragen: • Der Ordinatenabschnitt k1 ist derselbe für verschiedene E (z.B. Cl- oder Br-) • Der Anstieg k2 hängt sehr stark von der Natur von E ab! • Außerdem ist k2 10-100 mal so groß wie k1. • Substitution in quadratisch-planaren Komplexen vorwiegend durch einen assoziativen Mechanismus. 3 Beweise für den assoziativen Mechanismus • 1. schwacher Effekt der austretenden Gruppe • 2. starker Effekt der eintretenden Gruppe (= geschwindigkeitsbestimmender Schritt) • 3. negative Aktivierungsentropie Assoziativer Mechanismus für quadratisch-planare Komplexe wahrscheinlicher als für oktaedrische • Koordinationszahl niedriger, Komplex (zumindest potentiell) koordinativ ungesättigt • Die planare Anordnung lässt für einen eintretenden Liganden einen breit gewinkelten Zugang offen (ausser die planaren Liganden sind selbst sehr umfangreich) Stereochemie der quadratisch-planaren Substitution • Die Substitution in quadratisch-planaren Komplexen erfolgt immer unter Retention der Konfiguration (cis/trans). • Wenn eine stabile Zwischenverbindung in einem asynchronen assoziativen A Mechanismus auftritt, sollte diese eine trigonale Bipyramide sein, ebenso wie der ÜZ in einem synchronen Ia Mechanismus. Substitutions-Mechanismus für quadratisch-planare Komplexe mit Retention der Konfiguration Geometrie des fünffach koordinierten Übergangszustandes • Zunächst quadratische Pyramide mit dem eintretenden Liganden E an der Spitze • Danach Umlagerung in eine trigonale Bipyramide Obwohl außer Zweifel steht, dass quadratisch-planare Komplexe ihre Liganden durch einen assoziativen Mechanismus austauschen, gibt es doch signifikante Effekte der austretenden Gruppe. • Auch das Aufbrechen der Bindung M-D muss also geschwindigkeitsbestimmend sein, und es muss sich das Aufbrechen dieser Bindung im ÜZ bereits deutlich abzeichnen. • Dies ist konsistent mit unserem Bild des Mechanismus: • Ein Ligand in der äquatorialen Position einer trigonale Bipyramide hat andere Möglichkeiten der Orbital-Überlappung als derselbe Ligand im quadratisch-planaren Komplex: Dies kann einer Bindungslockerung entsprechen! Effekte der nichtreagierenden Liganden • Nicht nur der eintretende und der austretende Ligand haben Effekte auf die Reaktionsgeschwindigkeit. • Kinetischer Trans-Effekt (1926 entdeckt von Ilya Chernyaev, 1893-1966). Kommt in quadratisch-planaren Komplexen vor. Labilisierung des Liganden in trans-Stellung zu einem bestimmten Liganden. • Reihenfolge der trans-labilisierenden Fähigkeit: H2O<OH-<NH3≈py<Cl-<Br<I-<NO2-<SCN-<PR3≈H- ≈ SC(NH2)2<NO≈CO≈CN• Liganden mit hohem trans-labilisierenden Effekt nennt man transdirigierend. • Stereospezifische Synthesen, z.B. von cis-Platin Erklärung des trans-Effekts • Die trans-dirigierenden Liganden wirken umso stärker, je weichere LewisBasen sie sind. Z.B. sind CO und H- weiche Lewis-Basen mit starkem transdirigierendem Effekt, während H2O eine harte Lewis-Base ist • Das d8 - Metallion ist eine weiche Lewis-Säure und daher polarisierbar. Der trans-dirigierende Ligand polarisiert das Zentralion und schwächt damit die Bindung zum trans-stehenden Liganden • Beim Übergang vom quadratisch-planaren Komplex zum trigonal-bipyramidalen ÜZ bleibt der Ligand, der trans zu D steht, in der Äquatorialebene der trigonalen Bipyramide während die anderen beiden nichtreagierenden Liganden axial stehen • Die geometrischen Möglichkeiten für π-Überlappung sind sehr gut in der quadratischplanaren Anordnung. Im Durchschnitt hat jeder Ligand Zutritt zu 0.75 Metall–π– Orbitalen • Im trigonal-bipyramidalen ÜZ haben die axialen Liganden Zutritt zu 0.57 Metall–π– Orbitalen, und die äquatorialen Liganden zu 0.95 Metall–π–Orbitalen! • Ein π-bindender Ligand hat daher eine besondere Vorliebe dafür, in die Äquatorialebene des ÜZ zu gehen. Von den drei L bleibt derjenige, der schon vorher im quadratischplanaren Fall eine π-Bindung zum Metall hatte, in der Äquatorialebene. Gute πAkzeptor Liganden wie CO und C2H4 sind dementsprechend besonders stark transdirigierend. Reaktionen, die zu einer Änderung der Koordinationszahl führen (ohne Änderung der Oxidationszahl) • Substitutionsreaktionen können ohne nachweisbare Zwischenverbindung ablaufen, oder mit einer hochreaktiven Zwischenverbindung erhöhter oder erniedrigter Koordinationszahl • Im Prinzip könnten Reaktionen so modifiziert werden, dass aus den instabilen und hochreaktiven Zwischenstufen stabile Produkte mit erhöhter oder erniedrigter Koordinationszahl werden S ist ein axiales Lösungsmittel-Molekül. Falls es sich in der inneren Koordinationssphäre befindet, würde es sich um eine Substitutionsreaktion handeln, falls es sich in der äußeren Koordinationssphäre befindet, um eine Additions- bzw. Eliminierungsreaktion. Oszillierende Reaktionen Ein mechanisches System, z.B. ein Pendel, kann um seine Gleichgewichtslage schwingen. Ein chemisches System kann das nicht, denn zu allen Zeiten ist G >0 sobald das System sich vom Gleichgewicht entfernt . Oszillierende Reaktionen schwingen also fernab vom Gleichgewicht, während sie diesem zustreben. Konzentrationen von Zwischenverbindungen oszillieren und die Produkte entstehen mit oszillierenden Reaktionsgeschwindigkeiten. (1)Die Reaktionen laufen weit entfernt vom Gleichgewichtszustand ab (2)Die Reaktionen enthalten autokatalytische Schritte (3)Es gibt zwei stationäre Zustände Es gibt Beispiele für oszillierende Reaktionen in biochemischen Systemen. Die Erregung der Herztätigkeit z.B. kommt durch oszillierende Reaktionen zustande. Man beobachtet sie auch bei der Glykolyse. Wellenmuster in einem ReaktionsDiffusions-System, BelousovZhabotinsky Reaktion. Zhabotinsky, A.M., "Periodic liquid phase reactions," Proc. Ac. Sci. USSR 157,392 (1964). Zaikin, A.N. and Zhabotinsky, A.M., "Concentration wave propagation in twodimensional liquid-phase self-oscillating system," Nature 225, 535 (1970). Zhabotinsky,A.M.,and Zaikin,A.N., "Autowave processes in a distributed chemical system," J. Theor. Biol. 40, 45 (1973). Zhabotinsky, A. M., Eager, M. D., and Epstein, I. R., "Refraction and reflection of chemical waves," Phys. Rev. Lett. 71, 1526 (1993). Eine Spur Bromid muss zu Beginn vorhanden sein 7* ist keine Elementarreaktion, besteht aus einer Reihe von Elementarreaktionen Steady-state Näherung: d HBrO 2 0 v1 v2 v4 v5 2v6 dt d BrO 2 0 2v4 v5 dt 0 v1 v2 v4 2v6 k6 2 HBrO 2 k1 BrO3 Br k 2 HBrO 2 Br k 4 BrO3 HBrO 2 2 Quadratische Gleichung Chemische feedback-Schleife Für die Zwischenverbindungen resultieren zwei verschiedene steady-state Konzentrationen, die Verwirklichung der einen Lösung verursacht Änderungen im System, die bewirken, dass das System schließlich zur anderen Lösung überwechselt et vice versa. k1 BrO3 Br HBrO 2 1 k 2 Br k 4 BrO3 HBrO 2 2 k 4 BrO3 k 2 Br 2k6 Die steady-state Konzentrationen von BrO3- und Br- sind jeweils gekoppelt. Wenn die Bromidkonzentration einen kritischen Wert durchschreitet, wird der stationäre Zustand instabil, das System beginnt zu driften und „schaltet“ dabei von der einen Lösung zur anderen um. D.h. die Bromidkonzentration schwankt zwischen zwei kritischen Werten. Es handelt sich um ein komplexes irreversibles Phänomen das nur mit Hilfe der Thermodynamik irreversibler Prozesse theoretisch behandelt werden kann. Ilya Prigogine (1917-2003) was awarded the Nobel Prize in chemistry in 1977 for his contributions to nonequilibrium thermodynamics, particularly the theory of dissipative structures.