24.11.2009

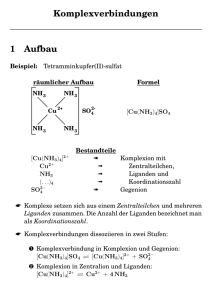
Werners Analysemethoden
Die Methoden, die Alfred Werner zur Erkenntnis führten, dass es Komplexe gibt, sind noch
heute gebräuchlich, allerdings nicht zur Strukturbestimmung. Die heute üblichen
spektroskopischen Untersuchungsmethoden waren damals unbekannt. Er benutzte
Leitfähigkeitsmessungen und Titrationstechniken zur Festlegung stöchiometrischer
Zusammenhänge, und die elementare Zusammensetzung konnte damals schon recht genau
durch Pyrolyse- und Verbrennungstechniken bestimmt werden. Dabei wurden die
Zersetzungsgase aufgefangen und quantitativ gemessen, eine Technik, die schon die
Lavoisiers perfektioniert hatten (und heute noch benutzt wird). Den Metallgehalt erhielt man
meist mit gravimetrischen Methoden, indem man das Metall nach Zersetzung der Verbindung
in eine bekannte Form, z.B. ein Oxid oder Sulfat überführte und dessen Masse genau
bestimmte.
Man muss hier anmerken, dass Werner in erster Linie so genannt kinetisch inerte Komplexe
studierte. Das war keine Absicht, aber auch kein Zufall. Die viel zahlreicheren kinetisch
labilen Komplexe lassen sich meist nicht in der Form, in der sie in Lösung vorliegen, als
Festkörper isolieren. Die kinetisch inerten Komplexe zerfallen ähnlich langsam wie
organische Moleküle, also kann man klar zwischen koordinierten Molekülen und Ionen und
solchen, die zur Erhaltung der Elektroneutralität vorhanden sind, unterscheiden. Jene
dissoziieren in der Lösung und können durch geeignete Reaktionen der qualitativen Analytik
direkt nachgewiesen werden, die am Metallion gebundenen hingegen nicht. Ausserdem kann
man diese Gegenionen zum Komplex titrieren, sofern eine geeignete Reaktion existiert, die
nicht durch den inerten Komplex gestört wird. Durch Messung der Aequivalentleitfähigkeit
(Leitfähigkeit pro Konzentrationseinheit) kann man alternativ erkennen, wie viele dissoziierte
Ionen vorliegen. Anhand der Feststellung, dass bei gleicher Zusammensetzung verschiedene
Farben auftreten können, schloss Werner auf das Vorhandensein von Isomeren. Man könnte
also behaupten, Werner habe „Spektroskopie“ im rudimentären Sinn eingesetzt.
Vorkommen von Metallkomplexen und Funktion
Metallkomplexe kommen an vielen Orten vor: In Mineralien, im Oberflächen- und
Grundwasser, in Organismen, und selbstverständlich in Gewerbe und Industrie. Am seltensten
sind sie in der Atmosphäre, es gibt wenige flüchtige Verbindungen dieser Art. Ebenso
1
vielfältig ist ihre Funktion: In Mineralien sind sie strukturbestimmende Bestandteile, im
Wasser sind sie schlicht die Formen, in denen Metallionen darin überhaupt existieren, in
Organismen sind sie Zentren in Katalysatorfunktionen (Enzyme). In der Technik dienen sie
ebenfalls als Katalysatoren, als Farbpigmente und vieles Andere.
Das Leben benötigt Kohlenstoff, Licht und Wasser. Ohne Metallkomplexe würde jedoch nicht
viel laufen: Die essentiellen Prozesse der Photosynthese und Zellatmung beruhen alle auf
Metallkomplexen, neben Tausenden von weiteren biochemischen Prozessen.
Bindungen in Komplexen
Das Auffälligste an den Metallkomplexen ist die in der Regel grosse Zahl von Bindungen an
einem zentralen Atom. Alfred Werner selbst hatte noch kein Modell dafür, die Geometrie der
Verbindungen bestimmte er nur über die von ihm so bezeichnete Koordinationszahl, das ist
die Zahl der unmittelbar am Metall gebundenen Liganden. Er argumentierte völlig korrekt,
dass sich die Liganden aus energetischen Gründen in eine Anordnung geringster
Raumforderung und Abstossung begeben würden. Für 6 Liganden ist das ein Oktaeder, für 4
ein Tetraeder. Ausserdem kennt man Komplexe mit 2 und 5 Liganden sowie 7-12 Liganden
bei sehr grossen Metallatomen. Eher selten ist die Koordinationszahl 3. Bei der
Koordinationszahl 4 wurden auch Strukturen gefunden, die quadratisch planar sind. Bei
näherer Betrachtung stellt sich bei diesen heraus, dass sie eigentlich Oktaeder sind, die auf
einer Achse keine oder nur sehr lose gebundene Liganden tragen.
Häufige Komplexformen mit je einem Beispiel:
2
5
[AgCl2]‾
Fe(CO)5
3
[HgI3]‾
[SnCl3]‾
4
6
[Co(NH3)6]3+
[Zn(NH3)4]2+
[Ni(CN)4]2‾
2
Die elektronische Natur der Metall-Ligand Bindung wurde bald als Interaktion von
nichtbindenden Elektronenpaaren der Liganden mit den an Elektronen defizitären
Metallzentren erkannt, i.a. fehlen ihnen zumindest die s- und p-Elektronen der Valenzschale,
und oft noch ein Teil der d-Elektronen der nächst tieferen Schale. Es gibt zwar Komplexe mit
tiefen Oxidationsstufen von Metallen, aber nur mit sehr speziellen Liganden und nicht in
Lösungsmitteln, die selbst als Liganden auftreten können. Eine Besonderheit ist auch das
gelegentliche Auftreten von C=C Doppelbindungen als Liganden anstelle von Atomen mit
nichtbindenden Elektronenpaaren. Wir kennen solche Bindungen schon von früher, sie
entsprechen dem Säure-Base Konzept von G. N. Lewis. Der Unterschied zu damals besteht
darin, dass der Elektronenpaar-Akzeptor, das Metall, mehrere Elektronenpaar-Donoren, also
Basen bzw. Liganden, binden kann. Tatsächlich binden die meisten Liganden auch H+.
Damit lassen sich die Bindungsverhältnisse mit dem VSEPR-Modell meist korrekt behandeln
wie bei kovalenten Verbindungen, obwohl die Bindungen selbst oft eher ionischen Charakter
besitzen. Je nach Koordinationszahl und Zahl der d-Elektronen sieht die Besetzung etwas
anders aus. Auf jeden Fall besetzen Ligand-Elektronenpaare zuerst die 4s- und 4p-Zustände
(bis zu 8 e−) im Metall (der 4. Periode), bevor weitere Elektronen in die 3d-Zustände gehen.
Sind die 3d-Zustände im Metall schon besetzt, so wird Besetzung der 4d-Zustände
angenommen. Das ist eher etwas unrealistisch, solche Komplexe haben ziemlich ionischen
Charakter.
Ti
Ti3+(H2O)6
FeCl4-
CoF63-
Co(NH3)63+
3d
4s
4p
4d
3d
4s
4p
4d
3d
4s
4p
4d
3d
4s
4p
4d
3d
4s
4p
4d
Metall-Elektronen
Donor-Elektronenpaare
3
LCAO-MO-Modell der Bindung in oktaedrischen, tetraedrischen und quadratisch-planaren
Komplexen: Wir kombinieren 4 oder 6 Ligandorbitale, i.a. vom s- oder σ-Typ, mit den 4s-
und 4p- Orbitalen des Metalls (aus der 4. Periode). Die 3d-Elektronen tragen normalerweise
nicht viel zum bindenden Anteil bei, die Bindungselektronen stammen, wie bei der normalen
Säure-Base Reaktion, ausschliesslich vom Donor (Base). Es existiert allerdings eine
Interaktion zwischen den d-Orbitalen, die auf die Donororbitale ausgerichtet sind. Diese ist
antibindender Art, die betreffenden d-Orbitale werden energetisch angehoben. Im Falle von
Koordinationszahl 6 sind dies im selben Ausmass das d x2 − y 2 und das d z2 Orbital. Im Falle des
quadratisch-planaren Komplexes ist es hauptsächlich das d x2 − y 2 Orbital und weniger das
d z2 Orbital. Bei Koordinationszahl 4 und tetraedrischer Geometrie werden die d xy , d xz und
d yz Orbitale energetisch ungünstig, dafür d x2 − y 2 und d z2 nicht. Nebenstehend ist das MO-
Schema eines
rel. Energie
4p
symmetrischen
oktaedrischen Komplexes
dargestellt, die bindenden
4s
Orbitale sind energetisch
3d
näher den LigandLiganden-MOs
Donororbitalen. Die
Energie der d-Elektronen
wird charakteristisch
aufgeteilt in drei
nichtbindende und zwei
schwach antibindende Zustände, wie vorgehend beschrieben. Das nächste Schema zeigt den
quadratisch planaren Fall,
wo nur noch 4
rel. Energie
4p
Ligandorbitale beteiligt
sind, was strenggenommen
nicht korrekt ist, weil es
4s
sich um gestreckte
3d
Liganden-MOs
Oktaeder handelt. Eine
tiefer gehende Behandlung
würde den Rahmen der
Basisvorlesung sprengen.
4
Detaillierte Betrachtungen sind späteren Spezialvorlesungen vorbehalten. Mit 4 Liganden und
tetraedrischer Geometrie
rel. Energie
4p
sieht das MO-Schema
nochmals anders aus, wie
links gezeigt. Hier kehrt
4s
sich die energetische
3d
Verteilung der dLiganden-MOs
Funktionen um, aus den
Gründen, die schon weiter
oben dargelegt wurden.
Die energetische
Verschiebung der d-
Elektronen hat wenig Einfluss auf die Ligandbindungsstärke, jedoch auf physikalische
Eigenschaften des Komplexes und sein reaktionskinetisches Verhalten.
Ligandfeld-Aufspaltung
Wie schon oben erwähnt, wird unter dem Einfluss der Donor-Elektronen der Liganden die
Energie der d-Zustände im Metall verändert. Die Liganden werden einerseits vom
Metallzentrum elektrostatisch angezogen, andererseits stossen sie sich mit der
Elektronendichte der d-Zustände ab. Besetzung dieser Zustände, wenn die Orbitalgeometrie
Vorzugsrichtungen auf die Bindungsachsen der Donoren aufweist, vermindert die Stabilität
des Systems. Das Phänomen wird Ligandfeldaufspaltung der d-Energien genannt. In einem
symmetrischen oktaedrischen Komplex wird der entstandene Energieunterschied ∆o genannt,
in einem symmetrischen tetraedrischen System ∆t. In der Regel ist ∆o > ∆t, weil 6 Liganden
ein stärkeres elektrisches Feld erzeugen als 4. Wenn ∆o grösser wird als die Energie, die es
kostet, zwei Elektronen mit antiparallelem Spin in einem Energiezustand unterzubringen
(Spin-Paarungsenergie), dann werden die d-Elektronen so weit wie möglich gepaart. Dadurch
verschwindet das magnetische Moment des Spins dieser Elektronen, und das gesamte
magnetische Moment des Metalls nimmt ab. Sind alle d-Elektronen gepaart, ist das Metall
diamagnetisch. Komplexe mit maximal gepaarten d-Elektronen nennt man low-spin, solche
mit maximal ungepaarten high-spin. Unterschiedliche Aufspaltung ∆o hat noch weitere
Folgen: Obwohl die Absorption eines Lichtquants (Photons) durch einen Übergang eines
Elektrons von einem d-Zustand zu einem andern d-Zustand quantenmechanisch verboten ist,
5
weil sich die Symmetrie des Elektronenzustands nicht ändert, gibt es eine
Restwahrscheinlichkeit dafür. Der Grund dafür
∆o < Ep
high spin
∆o
sind geringe Abweichungen von der perfekten
oktaederischen Form. Deshalb wird dennoch
etwas Licht von spezifischer Wellenlänge
absorbiert, was den Übergangsmetallkomplexen
ihre charakteristischen, aber nicht allzu kräftigen
∆o > Ep
low spin
∆o
stattfinden, diese Ionen sind farblos.
Farben verleiht. Das gilt auch für quadratisch-
planare und tetraedrische Komplexe. Ein noch
stärkeres Verbot betrifft die Spinumkehr bei der
Anregung von Elektronen. Bei einer d5-high spin
Konfiguration können deshalb keine Übergänge
hν
hν
d6 high spin
d5 high spin
Die d3 Konfiguration und die d6 low spin Konfiguration zeigen aufgrund ihrer hohen
Symmetrie eine bemerkenswerte Trägheit bei Austauschreaktionen von Liganden. Um einen
Liganden austreten und einen neuen eintreten zu lassen, müsste die hohe Symmetrie
kurzfristig aufgehoben werden. Dies geschieht nur selten, also ist die Reaktionsrate gering.
Diese Art Komplexe nennt man, wie schon erwähnt, kinetisch inert. Alfred Werners erste
Studienobjekte waren die d6 low spin Komplexe von CoIII.
d3
d6 low spin
Die Grösse von ∆o und ∆t hängt wesentlich von der Donorstärke der Liganden ab. Je stärkere
Lewisbasen sie sind, desto grösser wird die Aufspaltung der d-Energien. Grosse Aufspaltung
bedeutet dann Lichtabsorption bei kurzen Wellenlängen, weil viel Energie zur Anregung
6
benötigt wird. Es bedeutet auch Tendenz zu low spin Systemen, weil die Stabilisierung der
Bindung die Paarung der Elektronen erlaubt.
Reaktionen von Komplexen
Metallkomplexe gehen in erster Linie zwei Arten von Reaktionen ein:
Ligandaustauschreaktionen, die man auch als Lewis Säure-Base Reaktionen auffassen kann,
und Redoxreaktionen, die vor allem das Metallion betreffen.
[Cu(H2O)6]2+ + 4 NH3
⇀ [Cu(NH3)4]2+ + 6 H2O
↽
2 [Fe(CN)6]4– + Br2
⇀ 2 [Fe(CN)6]3– + 2 Br–
↽
Ligandaustausch
Redoxreaktion
Komplexgleichgewichte
Weil es sich bei Lewis Säure-Base Reaktionen immer um Gleichgewichte handelt, können wir
im Zusammenhang mit Komplexbildungsreaktionen und damit gekoppelten Vorgängen
wieder das Massenwirkungsgesetz anwenden. Die „Komplexbildung“ selbst ist eigentlich
eine Ligandaustauschreaktion. Geht ein festes Metallsalz in Lösung, so tritt das Metallkation
tatsächlich aus einem Komplex mit den Anionen (oder dem Kristallwasser) im Kristall über in
einen Komplex mit Lösungsmittelmolekülen. Gibt man dann zur Lösung einen Donor stärker
als das Lösungsmittel, wird dieses ausgetauscht und wir haben die „Komplexbildung“, wie sie
üblicherweise gemeint ist. Alle Komplexbildungen sind Stufenreaktionen, sofern mehr als ein
Ligand gebunden wird. Beispiel: Ein Metallion M2+ liegt hydratisiert vor und tauscht bei der
Zugabe des Liganden L mit steigender Konzentration das H2O gegen den Liganden aus. Wir
nehmen Koordinationszahl 6 an.
[M(H2O)6]2+ + L
[ML(H2O)5]2+ + L
[ML2(H2O)4]2+ + L
[ML3(H2O)3]2+ + L
[ML4(H2O)2]2+ + L
[ML5(H2O)]2+ + L
⇀
↽
⇀
↽
⇀
↽
⇀
↽
⇀
↽
⇀
↽
[ML(H2O)5]2+ + H2O
K1
[ML3(H2O)3]2+ + H2O
K3
[ML2(H2O)4]2+ + H2O
[ML4(H2O)2]2+ + H2O
[ML5(H2O)]2+ + H2O
[ML6]2+ + H2O
K2
K4
K5
K6
Falls der Ligand L ein Anion ist, ändert sich natürlich fortlaufend die Ladung. Oft kann man
die einzelnen K nicht richtig bestimmen, sondern nur Bruttoreaktionen bis zu einer
7
bestimmten Stufe. Die Bruttobildungskonstante bis zu einer Komplexbildungsstufe n
berechnet sich zu βn = K1 i K 2 i K 3 …i K n , wie man einfach durch Kombinieren der zu den K-
Werten gehörigen Massenwirkungsgesetze herausfindet. Die Konstanten nehmen in der Regel
mit zunehmendem Koordinationsgrad ab.
Komplexbildungsgleichgewichte können mit andern Gleichgewichten gekoppelt sein. Typisch
ist das für die Protonierungsgleichgewichte der Liganden. Mit Säure kann man manchen
Komplex wieder zerlegen. Beispiel:
⇀ [Cu(NH3)4]2+
Cu2+ + 4 NH3 ↽
NH4+
⇀ NH3 + H+
↽
lg K1 =4.25; lg K2 =3.61; lg K3 =2.98; lg K4=2.24
lg β4 =13.1
lg Ka = -9
Setzt man das MWG für die Säuredissoziation in das Brutto-Komplexbildungsgleichgewicht
ein, erhält man β4 =
β4
[Cu(NH 3 ) 24+ ][H + ]4
. Das kann man noch zu
[Cu 2+ ][NH 4+ ]4 K a4
K a4
[Cu(NH 3 ) 24+ ]
=
= β 4' umschreiben und erhält das pH-abhängige β4’. Bei pH = 4
[H + ]4 [Cu 2+ ][NH 4+ ]4
z.B. beträgt β4’ = β = 10
'
4
13.1
10 −36
M
= 10 −7.9 M −4 . Das bedeutet, dass bei diesem pH praktisch
−16
10
−4
kein Komplex existiert. Bei pH=9 sieht das anders aus, β = 10
'
4
Komplex ist voll ausgebildet.
13.1
10−36
M
= 1013.1 M −4 , der
−36
10
−4
Ein weiteres Beispiel demonstriert den Einfluss von Komplexbildungen auf
Elektrodenpotentiale. Das Standardelektrodenpotential für
Fe3+ + e–
⇀ Fe2+
↽
E 0Fe3+ / Fe2+ = 0.77V
weist Fe3+ als Oxidationsmittel aus. Komplexiert man Fe3+ mit dem Citration, dem Anion der
Zitronensäure, so sieht das ganz anders aus. Fe3+ bindet ein Citration mit K1 = 1012.
K1 =
[Fe(cit ) − ][H + ]
[Fe(cit ) − ][H + ]
12
3+
=
10
wird
aufgelöst
[Fe
]
=
und in die Nernstgleichung
[Fe3+ ][Hcit 3− ]
K1[Hcit 3− ]
eingesetzt: E = E 0Fe3+ /Fe2+ +
E = E 0Fe3+ / Fe2+ +
RT
[Fe(cit ) − ][H + ]
ln
Weil K1 eine Konstante ist, kann man
F
K1[Hcit 3− ][Fe 2+ ]
RT
1 RT [Fe(cit ) − ][H + ]
ln
+
ln
separieren und ein neues E°’ definieren:
F
K1 F
[Hcit 3− ][Fe 2+ ]
E 0' = E 0Fe3+ / Fe2+ +
RT
1
ln
= 0.77 V − 0.71V = 0.06 V . Das Elektrodenpotential wird nahezu 0!
F
K1
8
Wenn man dann noch einen hohen pH-Wert einstellt, kann man das Fe3+ in diesem Komplex
nur noch schlecht zu Fe2+ reduzieren, was beim Aqua-Ion kein Problem ist.
Auch Löslichkeitsprodukte werden beeinflusst. Kso(AgCl) = 10–10 M2 =[Ag+][Cl–], aber
β2 (AgCl2− ) = 105 M −2 =
[AgCl−2 ]
[Ag + ]
1
und
damit
=
. Man sieht, dass [Ag+]
−
+
− 2
[Ag ][Cl ]
[AgCl 2 ] β 2 [Cl− ]2
durch β2 und die [Cl–] abgesenkt werden, was bei genügend [Cl–] zur Unterschreitung des
Löslichkeitsprodukts führt, weil die Komplexbildung von [Cl–]2 abhängt, Kso aber nur linear.
Eine andere Darstellungsform dieses Sachverhalts zeigt die algebraische Umformung des
Komplexbildungs-MWG unter Separation des Ionenprodukts:
[AgCl −2 ]
[Ag ][Cl ] =
β2 [Cl− ]
+
−
Falls das Ionenprodukt links Kso überschreitet, findet Fällung statt. Unter hoher [Cl–] wird das
aber nicht der Fall sein, weil der Bruch rechts mit steigender [Cl–] immer kleiner wird.
[AgCl2–] ist begrenzt durch [Ag+]0, die totale Konzentration an Ag+, auch wenn immer mehr
Cl– zugefügt wird.
Spezielle Komplexformen
Rückbindung
Wenn ein Metallzentrum elektronenreich ist, was bei niedrigen Oxidatonszahlen gegeben ist,
so kann es bei bestimmten Liganden dazu kommen, dass das das Metall als Donor auftritt.
Das Donor-Orbital ist dann ein besetztes d-Orbital, das Akzeptor-Orbital kann ein π*-Orbital
oder ein unbesetztes d-Orbital eines Nichtmetalls der 3. oder höheren Periode sein. Es handelt
sich im zweiten Fall um ein ähnliches Phänomen wie die zu Beginn beschriebene
Hypervalenz in der Valenzbindungstheorie von Atomen in Perioden > 2. Ein typischer Ligand
mit π*-Rückbindung ist das Kohlenmonoxid CO, das Komplexe mit Übergangsmetallen der
Oxidationszahlen –I, 0, I und II bilden kann (Ni(CO)4, Fe(CO)5, Porphyrin-Fe(II)-CO, etc.).
Diese Bindungsart tritt in Ergänzung der σ-Donorbindung des Liganden auf, nicht allein.
9
C
CO π-Orbital (p kombiniert mit p)
besetzt
O
Metall d-Orbital
besetzt
C
O
C
O
CO π∗-Orbital (p kombiniert mit p)
unbesetzt
d - π∗ Rückbindung
Mehrzähnige Liganden – Chelate
Metalle binden mehrere Liganden, das ist soweit klar. Wenn das Metall aber mehrere
Bindungsstellen hat, kann ein Ligand mit mehr als einer Lewis Base-Funktion und geeigneter
Struktur auch mehrere dieser Bindungsstellen besetzen, und es entstehen Ringstrukturen. Den
Verbindungstyp nennt man Chelat, von griech. chelè, was „Klaue“ oder „Krebsschere“
bedeutet, weil der Ligand das Metall wie mit einer Zange „packt“. Die Basen eines mehrfach
bindenden Liganden werden auch Zähne genannt, es wird von mehrzähnigen Liganden
gesprochen. Auffällig dabei ist, dass die Stabilität mit der Zahl der Zähne zunimmt. Das
scheint zwar intuitiv richtig zu sein, kann aber dennoch auf verschiedene Weise begründet
werden. Die der Intuition näher stehende Begründung besagt, dass es sehr unwahrscheinlich
ist, dass sich mehrere Zähne zugleich ablösen, wenn der Ligand einmal gebunden ist. Die
Komplexbildung verläuft nämlich, experimentell belegt, auch für solche Liganden
schrittweise, und deshalb auch die Dissoziation. Weil der Ligand sich nicht auf einmal lösen
kann, ist die Wahrscheinlichkeit der erneuten Bindung eines dissoziierten Zahns hoch, also
kann sich der gesamte Ligand schlecht aus der Koordinationssphäre lösen.
Die zweite Begründung stützt sich auf die Entropie-Änderung ∆S bei der Komplexbildung.
Die Entropiefunktion eines molekularen Systems hängt von den so genannten BewegungsFreiheitsgraden ab. Davon existieren translatorische, rotatorische und vibratorische
Freiheitsgrade. Jedes Molekül hat 3 translatorische (Bewegung im Raum) sowie 2-3
10
rotatorische Freiheitsgrade (linear oder dreidimensional). Dazu kommen noch 3n-6
vibratorische Freiheitsgrade (3n-5 bei linearen Molekülen), wobei n die Zahl der Atome des
Moleküls ist. Diese Bewegungs-Freiheitsgrade machen die Fähigkeit eines Stoffs, Energie zu
speichern, aus. Die physikalische Grösse, die dies ausdrückt, ist die Wärmekapazität
 dS 
cp = T 
 . Ein normaler 2-zähniger Ligand beispielsweise hat 3 translatorische und 3
 dT  p
rotatorische Freiheitsgrade sowie die vibratorischen. Wenn er koordiniert wird, treten 2
Lösungsmittelmoleküle aus, die bis zu diesem Zeitpunkt keine eigenen translatorischen und
rotatorischen Freiheitsgrade hatten. Für den Verlust von 3 rotatorischen und 3 translatorischen
Freiheitsgraden des neuen Liganden werden je 2 mal 3 rotatorische und translatorische
Freiheitsgrade erzeugt, die Gesamtzahl der Freiheitsgrade des Systems steigt und damit seine
Entropie. Die vibratorischen Freiheitsgrade bleiben mehr oder weniger erhalten, weil sie ein
intramolekulares Phänomen sind. Weil ∆G = ∆H − T∆S und bei positivem ∆S das ∆G negativ
wird, bevorzugt die Entropieänderung den 2-zähnigen Liganden in der gebundenen Form, der
Komplex ist thermodynamisch stabiler als mit 2 einzähnigen Liganden.
Beispiele für mehrzähnige Liganden und ihre Komplexe:
NH2
H2N
O
O
1,2-Diaminoethan
Ethylendiamin (en)
O
-
-
O
+
O
NH
+
NH
OH
N
CH3
O
-
O
CH3
-
O
O
1,2- Dimethyl-3-hydroxypyrid-4(1H)-on
Deferipron
2-[2-(Bis(carboxymethyl)amino)ethyl-(carboxymethyl)
amino]acetat
Ethylendiamin-Tetraacetat (EDTA)
O
-
O
O
P
P
HO
Si
CH3
P
Tris(diphenylphosphanomethyl)-methylsilan
Siliphos
O
O
O
-
-
3-carboxylato-3-hydroxy-pentan-1,5dicarboxylat
Citrat
11
H2N
O
NH2
NH2
O
O
NH2
O
H2N
O
H2N
-
N
-
N
O
oktaedrischer tris-en Komplex
-
O
-
O
oktaedrischer EDTA-Komplex
O
O
H2O
O
3+
Fe
H2O
O
O
H2N
NH2
-
-
H2N
Cl
O
-
O
Fe(III)-Citrat-Komplex
Cl
-
Cl Cl
NH2
-
-
NH2
-
NH2
-
H2N
H2N
Enantiomerenpaar eines oktaedrischen
bis-en-dichlorido-Komplexes
Lewis Säuren – Basen Affinität
Um die Affinität („Vorliebe“) einer Base für Protonen zu charakterisieren, verwenden wir die
Dissoziationskonstanten Ka. Für Lewis Säure-Base Kombinationen existiert so etwas nicht. Es
lässt sich aber feststellen, dass gewisse Ligandtypen sich stärker an bestimmte Metalltypen
binden als an andere, es gibt also auch hier unterschiedliche Affinitäten. In den 1960er Jahren
verglich R. G. Pearson die Bildungskonstanten zahlreicher Komplexe mit den verschiedensten
Liganden. Dabei kam er zum Schluss, dass kleine, schlecht polarisierbare Ligandatome sich
stärker an kleine, stark geladene Metallionen binden als an solche mit niedriger Ladung und
grossem Radius. Umgekehrt bilden grosse, gut polarisierbare Ligandatome sehr stabile
Komplexe mit grossen, wenig geladenen Metallionen. „Gleich und gleich gesellt sich gern!“
Pearson nannte die grossen, gut polarisierbaren Ionen und Atome „weich“, wegen der
Beweglichkeit ihrer Elektronenhülle (entspricht der Polarisierbarkeit). Die kleinen, schlecht
polarisierbaren Partikel nannte er analog „hart“. Die Idee ist als „hart-weich Konzept der
Lewis Säuren und Basen“ oder HSAB (hard and soft acids and bases) bekannt geworden. Die
Regel ist gut brauchbar, z.B. bildet Al3+ (sehr hart) eigentlich nur stabile Komplexe mit F–
und O-Liganden (sehr hart). Cd2+ (weich) bildet stabile Komplexe mit R-S– Liganden
12
(Thiolate, weich), ebenso weich ist Ag+. Die Metallionen der Perioden 5 und 6 sind auf Grund
ihrer grossen Radien weich, ausser sie tragen Ladungen > +2. Sehr interessant ist der Effekt
bei Wechsel der Oxidationszahl des Metalls: Fe3+ ist wie Al3+ sehr hart und komplexiert
wirklich gut nur F– und O-Liganden. Nach der Reduktion zu Fe2+ ist die Stabilität mit F–
praktisch verschwunden, und O-Liganden werden nur noch schlecht gebunden. Dafür werden
jetzt Amin-Liganden angenommen, was Fe3+ nur tut, wenn auch noch O dabei ist, oder das
Ligandgerüst so steif wie bei einem Porphyrin. Amine gelten zwar noch als hart, sind das aber
schon viel weniger als O.
Eine Anomalie findet man bei niedrig geladenen Metallionen der 6. Periode. Au+, Hg2+ und
Pb2+ binden weiche Liganden sehr gut, aber merkwürdigerweise auch sehr harte wie OH– oder
Carboxylate R-COO–. Au+ reagiert mit H2O unter Freisetzung von H+, der pKa für diese
Reaktion ist 4, also saurer als Essigsäure, und das trotz der geringen Ladung von +1! Der
Grund dafür ist, dass sich hier Quantenmechanik und spezielle Relativität treffen: Das primäre
Akzeptororbital der genannten anomalen Ionen ist das 6s, das wie alle s-Funktionen eine
ziemlich hohe Dichte am bei diesen grossen Atomen hoch geladenen Kern besitzt. Die
eingespeisten Donorelektronen erfahren also eine sehr grosse elektrostatische Kraft.
Berechnet man die scheinbare Geschwindigkeit dieser Elektronen, so liegt der Wert nahe bei
der Lichtgeschwindigkeit. Ob sich diese Elektronen nun tatsächlich „bewegen“ oder nicht, der
relativistische Effekt der Zeitdilatation in Kernnähe ist vorhanden, damit halten sich die
Elektronen von aussen gesehen länger nahe am Kern auf als unter nicht-relativistischer
Betrachtung. Der Effekt bewirkt eine stärkere Bindung der Donorelektronen als unter nichtrelativistischen Bedingungen erwartet, das Ion ist eine starke Lewis Säure.
13
Anhang: Komplex-Isomere
Konstitutionsisomere
Ionisationsisomere
[Co(NH3)5(SO4)]Br oder [Co(NH3)5(Br)]SO4
Hydratisomere
[Cr(OH2)6]Cl3 oder [Cr(OH2)4Cl2 ]Cl•2H2O oder [Cr(OH2)5Cl ]Cl2•H2O
Koordinationsisomere
[PtII(NH3)4][PtIVCl6] oder [PtIV(NH3)4Cl2][PtIICl4]
Bindungsisomere
M − NO2 oder M − ONO
dioxidonitrato-κN oder dioxidonitrato-κO
M – CN oder M – NC
cyanido-κN oder cyanido-κO
M – SCN oder M – NCS
thiocyanato-κS oder thiocyanato-κN
Stereoisomere
Diastereoisomere
NH3
[PtCl2(NH3)2] cis und trans
Pt
NH3
[CoCl2(NH3)4] cis und trans
Cl
2+
Cl
-
NH3
-
Cl
Pt
Cl
2+
-
-
NH3
Enantiomere (Spiegelbild-Isomerie)
[CoCl2(en)2]+ und cis-trans
H2N
3+
Co
NH2
NH2
H2N
H2N
NH2
Cl
-
Cl
-
Cl Cl
-
-
NH2
3+
Co
H2N
H2N
Cl
3+
Co
NH2
NH2
Cl
-
NH2
14