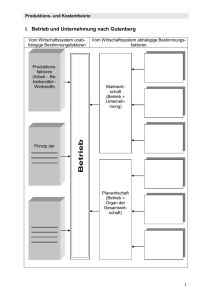
Betrieb und Unternehmung nach Gutenberg

Produktions- und Kostentheorie
I. Betrieb und Unternehmung nach Gutenberg
Vom Wirtschaftssystem
unabhängige
Bestimmungsfaktoren
Produktionsfaktoren
(Arbeit –
Betriebsmittel
- Werkstoffe
Marktwirtschaft
(Betrieb =
Unternehmung)
Betrieb
Prinzip der
___________
___________
___________
Vom Wirtschaftssystem abhängige
Bestimmungsfaktoren
Planwirtschaft
(Betrieb =
Organ der
Gesamtwirtschaft)
___________
___________
___________
___________
1
Produktions- und Kostentheorie
II. Produktionstheoretische Grundlagen
1. Produktionstheorie
Produktionsfaktoren
Produktion
Produkte
Input
Throughput
Output
Produktionsprozess





Theoretisches Aussagesystem, das sich mit den wirtschaftlichen Prozessen der
Herstellung von Produkten (Gütern) befasst.
Insbesondere werden die quantitativen Beziehungen der eingesetzten
Produktionsfaktoren und ausgebrachten Produkte untersucht.
Ziel: Funktionale Zusammenhänge (Regelmäßigkeiten) zwischen der Menge der
eingesetzten Produktionsfaktoren und der damit hergestellten Produkte
aufzeigen.
Primärer Aspekt: Mengenbewegungen im gesamten Produktionsprozess
Produktionsfunktion: Funktionaler Zusammenhang zwischen Input und Output
2. Kostentheorie
Kostentheorie – Wert
Produktionstheorie - Menge






Aufbauend auf dem in der Produktionstheorie entwickelten Mengengerüst des
Produktionsprozesses wird in der Kostentheorie durch Einbeziehung des
Produktionsfaktorpreises das zugehörige Wertgerüst untersucht.
Betrachtung der Beziehung zwischen den mit Preisen bewerteten
Produktionsfaktoren und des damit erzeugten Outputs.
Ziel: Funktionale Zusammenhänge (Regelmäßigkeiten) zwischen dem Wert der
eingesetzten Produktionsfaktoren und den damit hergestellten Produkten
aufzeigen.
Primärer Aspekt: Wertbewegungen im Produktionsprozess
Kostenfunktion: Funktionaler Zusammenhang zwischen bewertetem Input
(Wert) und Output (Menge)
Minimierungsprinzip: ______________________________________________
_________________________________________________________________
_________________________________________________________________
2
Produktions- und Kostentheorie

Maximierungsprinzip: ______________________________________________
_________________________________________________________________
_________________________________________________________________
3. Zusammenhang: Produktions- /Kostentheorie
Ökonomisches Prinzip
 Ein vorgegebener Output soll mit so _______ Produktionsfaktoren (Input) wie
möglich hergestellt werden.
 Keine Verschwendung von Produktionsfaktoren = technische Effizienz
Produktionstheorie: Technische Effizienz
 Bestimmte Kombinationen von Produktionsfaktoren können einen vorgegebenen
Output sinnvoller erzeugen als andere Kombinationen. Es existieren alternative
Produktionsfaktor-Kombinationen / Produktionsprozesse.
 Die Produktionstheorie sondert die technisch ineffizienten Produktionsprozesse
aus und identifiziert diejenigen, die im Hinblick auf das ökonomische Prinzip
optimal sind.
Kostentheorie: Ökonomische Effizienz
 Die Kostentheorie identifiziert denjenigen technisch effizienten
Produktionsprozess, der zu den minimalen Kosten für einen vorgegebenen
Output führt (____________________________________________).
 Ergebnis: ökonomisch effizienter Produktionsprozess
 Erst die Bewertung der Produktionsfaktoren führt zu einer Vereinheitlichung der
Rechengrößen. Erst diese Vereinheitlichung über Geldeinheiten erlaubt die
Auswahl des kostenminimalen Produktionsprozesses unter mehreren technisch
effizienten Alternativen.
4. Produktionsfunktion
Produktionsfunktion: allg. verbal
 Darstellung des funktionalen Zusammenhangs zwischen Input und Output bei
technisch effizienter Produktion (d.h. keine Verschwendung von
Produktionsfaktoren)
Produktionsfunktion: allg. formal
 Voraussetzung: beliebige Teilbarkeit und Homogenität aller Produktionsfaktoren
(Input) und Produkte (Output)
 m = Output = Produkte, Ausbringungsmenge
 r = Input = verschiedene Produktionsfaktorarten 1 – n
_________________________________________

Prämisse: (nur) zwei verschiedene Produktionsfaktor-Arten
______________________________________

Für jede denkbare technisch effiziente (Produktions-)Faktorkombination wird die
Höhe der dazugehörigen Ausbringungsmenge angegeben.
3
Produktions- und Kostentheorie

Hinsichtlich der Beziehung zwischen den Faktorarten innerhalb einer
Produktionsfunktion lassen sich zwei Arten von Produktionsfunktionen
unterscheiden: substitutionale und limitationale Produktionsfunktionen
5. Substitutionalität - Limitationalität
Merkmale der Substitutionalität
 Ein vorgebener Output kann durch verschiedene Kombinationen der (beiden)
Produktionsfaktoren erzeugt werden.
 D.h.: Produktionsfaktoren können im Produktionsprozess gegeneinander
________________________________ werden.
 Bsp.: Zum Teeren eines Straßenstücks von 200 Meter Länge an 1 Tag (= m)
können entweder 4 Arbeiter (= r1) und 2 Teermaschinen (= r2) oder _____
Arbeiter und nur ________ Teermaschine eingesetzt werden.
 D.h.: Die Verringerung der Einsatzmenge eines Faktors kann bei Konstanz der
Ausbringungsmenge durch den verstärkten Einsatz eines (des) anderen Faktors
_____________________________ werden.
 Auch: Die Ausbringungsmenge kann durch eine veränderte Einsatzmenge nur
eines Faktors bei Konstanz aller (des) anderen Faktors beeinflusst werden.
 Bsp.: 4 Arbeiter teeren mit 3 Teermaschinen 300 Meter am Tag.
 ________________________________________: Zur Herstellung einer
bestimmen Ausbringungsmenge muss von jeder Faktor-Art stets eine positive
Einsatzmenge verwendet werden. Die Faktoren sind somit nicht vollkommen
substituierbar.  Bsp.: Pulvertee
 ____________________________________________: Bei der Herstellung einer
bestimmten Ausbringungsmenge ist die eine Faktor-Art durch die andere
vollständig ersetzbar.
Merkmale der Limitationalität
 Ein vorgegebener Output kann nur durch _______________ effiziente
Kombination der (beiden) Produktionsfaktoren erzeugt werden.
 D.h.: Die beteiligten Produktionsfaktor-Arten stehen in einem technisch
bindenden Verhältnis zueinander und zur Ausbringungsmenge und lassen sich
nicht gegenseitig substituieren.
 Bsp.: Zur Herstellung eines Fahrrads (= m) ist die Kombination von ___ Rädern
(=r1) und ___ Sattel (= r2) technisch effizient. Durch den ausschließlichen Einsatz
weiterer Sättel kann kein einziges Fahrrad mehr produziert werden.
 D.h.: Nur durch den vermehrten (verringerten) Einsatz ________ Faktoren kann
eine erhöhte (verringerte) Ausbringungsmenge erzielt werden (anderes
„Produktionsniveau“).
 Bsp.: _____ Räder und 2 Sättel zur Herstellung von _____ Fahrrädern.
4
Produktions- und Kostentheorie
6. Produktionsfunktion vom Typ A (s. VWL)
Historischer Hintergrund:
 Entwicklung von Turgot um 1766
 Empirisch, statistisch überprüft von Thünen um 1842
 Später von Gutenberg unter dem Namen „Gesetz vom abnehmenden
Ertragszuwachs“ oder „Ertragsgesetz“ in die Betriebswirtschaftslehre
übernommen.
Sachlicher Hintergrund:
 Landwirtschaftliche Produktion historisch bedingt als alleiniger
Anwendungsbereich
 _________________ Substitutionalität: Eine Verringerung der Bodenfläche kann
durch den Einsatz von mehr Dünger oder mehr Saatgut kompensiert werden;
ohne Boden oder Saatgut ist jedoch keine Ernte zu erwarten.
 Beobachtung von Turgot: Der zunehmende Einsatz des Faktors Arbeit bei
konstanten Einsatzmengen der Faktoren Boden, Saatgut und Dünger führt
zunächst zu steigenden und später zu abnehmenden Grenzerträgen bei der
Ernte.
 ______________________ Faktorvariation: Abhängigkeit der Ernte von der
Einsatzmenge eines Produktionsfaktors (Arbeit) bei Konstanz der übrigen
Produktionsfaktoren (Boden, Saatgut, Dünger)
E / GE / DE
Ertragsgesetz
I
II
III
IV
C
B
E
A
GE
DE
r2 (Arbeit)
Modell-Prämissen
 Periphere Substitutionalität und partielle Faktorvariation
 1 konstanter Produktionsfaktor (homogen, beliebig teilbar)
 1 variabler Produktionsfaktor (homogen, beliebig teilbar)
 Herstellung eines (1) Produktes (homogen, beliebig teilbar)
 1-stufige Produktion mit konstanter, bekannter Produktionstechnik
5
Produktions- und Kostentheorie
Beobachtete Größen
 Gesamtertrag m: Absolute Erträge; ermittelt aus der Produktionsfunktion bei
Variation eines (1) Faktors (hier r2) und unter Konstanz des anderen (1) Faktors
(hier r1)  partielle Gesamtertragskurve
 Grenzertrag M: Ertragszuwächse bei infinitesimalen Änderungen des variablen
Faktors (hier r2) und Konstanz des anderen Faktors (hier r1)  partielles
Grenzprodukt bzw. Grenzproduktivität des variablen Faktors; ermittelt durch die 1.
Ableitung der part. Gesamtertragsfunktion
 Durchschnittsertrag e: Durchschnittliche Erträge; ermittelt über die Division des
Gesamtertrages durch die jeweils dafür eingesetzte Menge des variablen Faktors
(hier r2)  partielle Durchschnittsertragsfunktion
Gesamertrag
Grenzertrag
Durchschnittsertrag
Phase

I



II

III


IV

=
= GP =
=
Beobachtungen
Der anfängliche Mehreinsatz von Arbeit zur Pflege des Ackers (z.B.
Unkraut entfernen) bewirkt eine üperproportionale Erhöhung der Ernte.
steigende Erntezuwächse bis r2 bei A
Ab r2 bei A ist ein Großteil des Unkrauts entfernt; weitere Pflegearbeit
bewirkt jedoch nur eine unterproportionale Erhöhung der Ernte.
sinkende Erntezuwächse (Grenzerträge m’); jeder zusätzliche Arbeitstag
zur Pflege lässt zwar die Gesamternte anwachsen, diese Zuwächse
werden jedoch mit jedem zusätzlichen Arbeitstag geringer, da das
entfernte Unkraut das Wachstum des Weizens immer weniger
behinderte.
Ab r2 bei B bewirkt der Mehreinsatz von Arbeit weiterhin eine
unterproportionale Erhöhung der Ernte. Das hier entfernte Unkraut war
dem Wachstum des Weizens noch weniger hinderlich.
Sinkende Erntezuwächse; jeder zusätzliche Arbeitstag lässt zwar die
Gesamternte anwachsen, diese Zuwächse werden jedoch weiterhin mit
jedem zusätzlichen Arbeitstag geringer.
Ab r2 bei C bewirkt der Mehreinsatz von Arbeit eine Verringerung der
Ernte, da die Feldarbeiter beim Unkraut jäten mehr jungen Weizen
zertrampeln als die Pflege dem Wachstum nützlich ist.
Negative Erntezuwächse; jeder zusätzliche Arbeitstag lässt die
Gesamternte sinken.
6
Produktions- und Kostentheorie
Phase
Gesamtertrag E
Grenzertrag GE
Durchschnittsertrag DE
Endpunkte
I
II
III
IV
III. Kostentheoretische Grundlagen
1. Kosten


Kosten stellen den mit Preisen bewerteten Verzehr von Produktionsfaktoren dar
Bewertung erfolgt durch Multiplikation der Produktionsfaktoren mit den vom Markt
vorgegebenen Preisen
2. Gesamtkosten


Gesamtkostenfunktion K ergibt sich durch Multiplikation der eingesetzten Mengen
an Produktionsfaktoren r mit ihren Preisen p
K=
Faktoreinsatzmengen hängen von der Ausbringungsmenge m ab 
Gesamtkosten hängen ebenfalls von der Ausbringungsmenge m ab

m=

K=
3. Fixe und variable Kosten
Fixe Kosten
 Bevor ein Betrieb die Produktion aufnehmen kann, muss die ________________
_________________________ hergestellt werden. Beispiele: Kauf oder Miete
von Gebäuden, Fuhrpark, Maschinen, Werkzeug; Abschluss von Versicherungen
oder Lieferverträgen.
7
Produktions- und Kostentheorie

fallen unabhängig von der Produktionsmenge bzw. dem Beschäftigungsgrad in
gleicher Höhe an
absolut fixe Kosten (Grundbereitschaftskosten)
 stets unverändert
 unabhängig von Veränderungen der Gesamtkapazität
relativ fixe Kosten (Zusatzbereitschaftskosten, auch: sprungfixe / intervallfixe
Kosten)
 steigen mit der Kapazitätsausdehnung
 z.B. Abschreibung zusätzlicher Maschinen; menschliche Arbeit steht nur in
Form von Vollzeitkräften mit 40 Stunden Arbeitszeit/Woche zur Verfügung
(kleinere Einheiten durch Teilzeitarbeit)



Sprungfixe Kosten
60
Kosten
50
40
K*
30
K
20

10
0
0
2
4
6
8
Arbeiter
Jede vollständige Einheit eines
Produktionsfaktors (z.B.
Vollzeitkraft) muss vollständig
bezahlt werden  die
Mengensprünge der
Produktionsfaktoren verursachen
daher Sprünge der tatsächlichen
Kostenkurve K
die Kurve K* zeigt die
kontinuierliche
Kostenentwicklung bei beliebig
teilbaren Produktionsfaktoren
Variable Kosten
 Kosten, die von der Höhe der __________________________ abhängig sind,
werden als variable Kosten bezeichnet
 Beispiel: Je mehr Autos ein Betrieb produziert, desto mehr Rohbleche, Reifen
und z.B. höhere Akkordlöhne werden erforderlich.
Gesamtkosten = fixe und variable Kosten
K
K
Kf
Kv(m)
=
=
=
=
Kf + Kv(m)
Gesamtkosten
fixe Kosten
variable Kosten
Grenzkosten
Als Grenzkosten wird die Veränderung der Gesamtkosten aufgrund einer
infinitesimal kleinen Änderung des Outputs bezeichnet. Sie werden durch die 1.
Ableitung K’(x) der Kostenfunktion K(x) ermittelt.
Allg. gilt: f(x) = axn+c
f’(x) = n*axn-1
 s. Beispiel zu Gesamt-/Grenz-/Stückkosten
Mathematische Herleitung der Kostenfunktion:
8
Produktions- und Kostentheorie
Annahmen: 




2 Produktionsfaktormengen r1 und r2
Limitationalität
Preise p1 und p2
Fertigungsmenge x
fixer Kostenfaktor Kf
Kosten für r1: K1 =
Kosten für r2: K2 =
Es gilt: r1 =
und r2 =
Produktionskoeffizenten
, wobei a1 und a2 sog.
Der Produktionskoeffizient gibt den Anteil eines Produktionsfaktors an, der bei der
Produktion auf eine Einheit des Outputs entfällt: a1 =
und a2 =
Bei linear-limitationalen Produktionsfunktionen sind die Produktionskoeffizienten
technische Konstante.
Gesamtkosten = variable Kosten + fixe Kosten
=
=
=
Bei m = a1 * p1 + a2 * p2 und b = Kf gilt:
K=
1
x  3 (vgl. allg. Geradengleichung in der Mathematik: y = mx + b)
2
Gesamtkosten
Beispiel: K 
x
0
1
2
3
4
5
6
7
8
9
10
Kv
Kf
K
K, Kf, Kv
9
8
7
6
5
4
3
2
1
0
9
Produktions- und Kostentheorie
Stückkosten
kv
kf
k
4,00
3,50
3,00
k, kv, kf
x
1
2
3
4
5
6
7
8
9
10
2,50
2,00
1,50
1,00
0,50
0,00
0
1
2
3
4
5
6
7
8
9
10
11
x
4. Beispiel zu Gesamt-/Grenz-/Stückkosten
Ein Betrieb benötigt 200.000,00 € zur Herstellung der Betriebsbereitschaft. 40,00 €
werden pro Ausbringungsmengeneinheit an variablen Kosten aufgewendet. Es sollen
2.000 Ausbringungsmengeneinheiten (m) produziert werden.
Gesamtkostenfunktion K =
Gesamtkosten K =
Grenzkostenfunktion K’ =
Grenzkosten K’ =
Stückkostenfunktion k =
Stückkosten k =
variable Stückkostenfunktion kv =
10
Produktions- und Kostentheorie
variable Stückkosten kv =
Fixe Stückkostenfunktion kf =
Fixe Stückkosten kf =
5. Der Zusammenhang zwischen Kosten, Erlösen und Gewinn
Gesamtkostenfunktion: K 
p  1,25
Kv 
x
0
1
2
3
4
5
6
7
8
K
K, E, Kv, G/V in Tsd.
1
x  3 ; Kapazitätsgrenze = 8
2
k
E
E
Kv
G/V
1
2
3
x
0
1
2
3
4
5
6
7
8
K'
k
p
kv
K'
12
10
8
6
4
2
0
-2
-4
0
4
5
6
7
8
9
x in Tsd.
K
E
Kv
G/V
11
Produktions- und Kostentheorie
Bei welcher Stückzahl decken die Erlöse die Kosten (Nutzenschwelle)?
k, kv, p in Tsd.
4
3
2
1
0
0
1
2
3
4
5
6
7
8
9
x in Tsd.
k
p
kv
Welche Kostenkurven schneiden sich im Punkt A? ___________________________
______________________________________________________________
Im __________________________________ wird der maximale Gewinn erzielt.
Welche Stückzahl sollte das Unternehmen daher produzieren?
_______________________________________________________: Würde die
Produktmenge zu einem Preis in dieser Kostenhöhe abgesetzt, entstünde ein Verlust
in Höhe der fixen Kosten, den ein Unternehmen nur für kurze Zeit hinnehmen kann.
Bei einem Preis, der diese Kostenhöhe unterschreitet, würde der Betrieb stillgelegt.
Wo liegt das Betriebsminimum / die Preisuntergrenze im obigen Schaubild?
12
Produktions- und Kostentheorie
6. Linearer Gesamtkostenverlauf und linearer Gesamterlösverlauf
Typische Erlös-Kosten-Situationen und ihre Konsequenzen
Kostendeckung bei
Kapazitätsauslastung
 Verlust wenn x < xmax
Verlust in Höhe der fixen
Kosten
Konsequenz /
Handlungsempfehlung
Nach Möglichkeit Produktion
bis zur Kapazitätsgrenze
ausweiten
Nach Möglichkeit Produktion
bis zur Kapazitätsgrenze
ausweiten
Suche nach alternativen und
billigeren
Produktionsverfahren
Die Aufrechterhaltung der
Produktion lohnt gerade noch

Betriebsstilllegung
Situation
Auswirkung auf Erfolg
I.
E > K, p > k
Gewinnerzielung
II.
p = k, E = K
bei x < xmax
Erfolg = 0
III.
p = k, E = K
bei x = xmax

IV. p = kv, E =KV
 Betriebsminimum
V. p < kv, E < Kv

Verlust bei Stilllegung ist
kleiner als bei Fortführung
der Produktion
Grenzkosten > Grenzerlös
Break-Even-Point-Analyse
Ermittlung jener Produktmenge, bei der die Kosten gleich dem Erlös sind, so dass
weder Gewinn noch Verlust entsteht.
Bsp.: BEPA für Herstellung von Bürostühlen
Kv = 200,00 €; Kf = 250.000,00 €; VP = 450 €
Drei Möglichkeiten zur Ermittlung des BEP:
a) tabellarisch
x
Kf
Kv
KG
E
G/V
0
600
1000
1400
13
Produktions- und Kostentheorie
 bei x = ________________ gilt: E = KG  BEP
b) rechnerisch
Gesamtkosten KG (x) = ________________________
Gesamte variable Kosten Kv (x) = ____________________
E(x) = ________________
algebraische Lösung:
im Beispiel: x = ______________________________________
Kosten/Erfolg
c) grafisch
700000
600000
500000
400000
300000
200000
100000
0
-100000
-200000
-300000
0
500
1000
1500
BEP liegt im Schnittpunkt von Erlös- und Kostengeraden
x
Kf
Kv
KG
E
G/V
14
Produktions- und Kostentheorie
Nutzkosten und Leerkosten
Nutzkosten KNutz:
Leerkosten KLeer:
Teil der Fixkosten, der der tatsächlich genutzten Kapazität
zuzurechnen ist.
Teil der Fixkosten, der auf nicht genutzte Kapazität entfällt.
Kfix = KNutz + KLeer
KNutz =
wobei B = Beschäftigung
und Bmax = Kapazität
alternative Ermittlung der Leerkosten:
KLeer =
KLeer = Kfix - KNutz
=
=
Beispiel:
fixe Kosten: 100.000,00 €
Maximalkapazität: 5000 Stück
Produktionsmenge
0
500
1000
1500
2000
2500
3000
3500
4000
4500
5000
Beschäftigungsgrad
Kfix
Knutz
Kleer
15
Produktions- und Kostentheorie
120.000,00 €
Kosten in €
100.000,00 €
80.000,00 €
60.000,00 €
40.000,00 €
20.000,00 €
-
€
0
20
40
60
80
100
Beschäftigungsgrad in %
Kostenremanenz (auch: Kostenresistenz)
Kostenverlauf im Fall rückläufiger Beschäftigung, bei der die Gesamtkosten vielfach
nicht auf der gleichen Kostenkurve Ka zurücklaufen, mit der sie vorher bei steigender
Beschäftigung zugenommen haben. Sie fallen entsprechend einer darüber liegenden
Kostenkurve Kr. Die höheren Kosten werden als remanente Kosten bezeichnet.
Ursachen: Andersartige Anpassung bei Beschäftigungsabnahmen als bei
Beschäftigungszunahmen aus arbeitsrechtlichen, wirtschaftlichen, sozialen,
betriebspolitischen, arbeitsorganisatorischen oder psychologischen Gründen. Die
Kostenremanenz sollte deshalb nicht unbedingt als ein Nachhinken der Kosten bei
Beschäftigungsrückgang, sondern als ein Wirksamwerden anderer Kostenbestimmungsfaktoren aufgefasst werden. Die Kostenremanenz kann als Remanenzschleife
(Hysteresis-Schleife, vgl. Abbildung „Kostenremanenz (1)”) oder als remanenter
Kostensprung auftreten (vgl. Abbildung „Kostenremanenz (2)”).
16
Produktions- und Kostentheorie
Der Hysterese-Effekt beschreibt die
Fortdauer einer Wirkung bei Wegfall der
Ursache: Aufgebaute Kapazitäten können
nicht auf der ursprünglichen Kostenkurve
abgebaut werden, auf der sie vorher bei
steigender Beschäftigung zugenommen
haben.
IV. Ertragsgesetzliche Kostenfunktionen unter Zugrundelegung
einer Produktionsfunktion vom Typ A
1. Beispiel für einen ertragsgesetzlichen Kostenverlauf
K
Kostenfunktion: K = ax3 + bx2 + cx + d
17
Produktions- und Kostentheorie
2. Ermittlung der Durchschnittskosten
ertragsgesetzlicher
Kostenverlauf
allgemein
Gesamtkosten K
Durchschnittskosten
k
variable Stückkosten kv
fixe Stückkosten kf
3. Übungsaufgabe
Gesamtkosten K 
Stückkkosten k 
var iable Stückkosten kv 
Grenzkosten K ' 
x
K
k
kv
K'
kf
0
1
2
3
4
5
6
7
8
18
Produktions- und Kostentheorie
200
180
160
K,k,kf,kv,K'
140
120
100
80
60
40
20
0
0
2
4
6
8
x
K
k
kv
K'
Stückkostenanalyse
90
80
70
K,k,kf,kv
60
50
40
30
20
10
19
0
0
2
4
6
x
8
10
Produktions- und Kostentheorie
Ermittlung des Betriebsminimums:
Das Betriebsminimum liegt im Minimum der durchschnittlichen variablen Kosten.
Würde die Produktmenge zu einem Preis in dieser Kostenhöhe abgesetzt, entstünde
ein Verlust in Höhe der fixen Kosten, den ein Unternehmen nur für kurze Dauer
hinnehmen kann. Bei einem Preis, der diese Kostenhöhe unterschreitet, würde der
Betrieb stillgelegt.
Welche Kurven schneiden sich im Betriebsminimum?
__________________________________________________________________
Gleichsetzen der entsprechenden Kostenfunktionen:
20
Produktions- und Kostentheorie
Zusammenfassende Darstellung
220
200
180
160
D
140
K,k,kv,K',E,p
120
100
80
A
60
B
40
A
20
C
D
B
E
0
0
2
4
6
8
-20
-40
x
K
k
kv
K'
E
p
G/V
21
Produktions- und Kostentheorie
Kurvenbereich
A: Nutzenschwelle
Erläuterung
B: Nutzenmaximum =
Gewinnmaximum
C: Kostenoptimum =
Betriebsoptimum
D: Nutzengrenze
E: Betriebsminimum
22