Fixkostenproportionalisierung

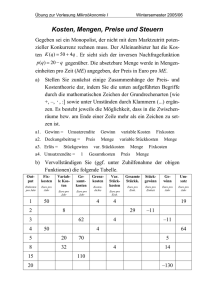
Das Problem der Fixkostenproportionalisierung
Für ein Produkt gelten folgende Beziehungen:
(1)
U  p x
(2)
K  KF  K V
(3)
k
(4)
kF 
KF
x
(5)
kV 
KV
x
(6)
G  U K
(7)
g
U 
Umsatz
p 
Preis
x 
Menge
K 
Kosten
KF 
fixe Kosten
KV 
variable Kosten
k 
Stückkosten
kF 
fixe Stückkosten
kV 
variable Stückkosten
G 
Gewinn
g 
Stückgewinn
K
x
G
x
wobei
[const.]
[const.]
Kennt man den Stückgewinn, so liegt der Gedanke nahe, mithilfe des Stückgewinns auszurechnen,
wie sich der Gesamtgewinn ändert, wenn die Produktmenge geändert wird. Man könnte nämlich einfach den Stückgewinn mit der Mengenänderung x multiplizieren:
(8)
G  g  x
Die Frage ist aber, ob dies richtig ist. Um dies herauszufinden, wird Gleichung (8) mit Hilfe der obigen
Gleichungen umgeformt.
Gleichung (7) in (8) eingesetzt:
-1-
582629546
Das Problem der Fixkostenproportionalisierung
G 
G
 x
x
Hierin (6) eingesetzt:
G 
UK
 x
x
Hierin (2) eingesetzt:
G 
U  KF  K V
 x
x
Hierin (1), (4) und (5) eingesetzt:
G 
p  x  kF  x  k V  x
 x
x
G  (p  k V  kF )  x
(9)
G  (p  k V )  x  kF  x
Ob sich der Gewinnunterschied G(x) tatsächlich so ergibt, sieht man, wenn man den Gewinn vor
und nach der Mengenänderung explizit formuliert.
Es gelte
x0 
Menge vor der Änderung
x1 
Menge nach der Änderung
x 
x1 x0
Somit gilt für den Gewinn in der Ausgangslage
G0  p  x0  k V  x0  KF
(10)
G0  (p  k V )  x0  KF
und nach Veränderung der Menge auf x1 unter Beachtung der Konstanz von p und kV
G1  p  x1  k V  x1  KF
(11)
G1  (p  k V )  x1  KF
Die Formulierung des Gewinns nach Gleichung (10) und Gleichung (11) teilt den Gewinn auf in die
Komponente, die von der Menge abhängt, nämlich (p kV)·x, und die Komponente, die nicht von x
abhängt, nämlich KF. Die von x abhängige Komponente wird als Deckungsbeitrag (DB) bezeichnet.
Dieser kann auch auf das einzelne Produkt bezogen werden, und man erhält den Deckungsbeitrag pro
Stück p  kV.
Somit lässt sich der Gewinn auch formulieren als
(10a)
G0  DB p. St.x0  KF
(10b)
G0  DB(x0 )  KF
-2-
582629546
Das Problem der Fixkostenproportionalisierung
und entsprechend
(11a)
G1  DB p. St.x1  KF
(11b)
G1  DB(x1)  KF
Es kann nicht verwundern, dass die Gewinnänderung, die sich durch eine Mengenänderung ergibt, nur
von der variablen Gewinnkomponente abhängt und nicht von den Fixkosten. Für die Gewinndifferenz
gilt nämlich
G1  G0  (p  k V )  x1  KF  (p  k V )  x0  KF
G1  G0  (p  k V )  (x1  x0 )
(12)
G  (p  k V )  x
Dies ist die richtige Gewinnänderung. Man kann auch sagen: Die Gewinndifferenz, die durch eine
Mengenänderung bewirkt wird, ergibt sich aus dem Deckungsbeitrag pro Stück, multipliziert mit der
Mengenänderung:
(12a)
G  DB p. St.x
Vergleicht man nun die richtige Gewinndifferenz nach Gleichung (12) mit der Gewinndifferenz nach
Gleichung (9), so unterscheiden sich diese um den Betrag
k F  x
Dies sind die fixen Stückkosten der Ausgangslage, multipliziert mit der Mengenänderung.
Um diesen Betrag wird nach Gleichung (9) falsch gerechnet – es wird unterstellt, dass die fixen
Stückkosten, multipliziert mit der Mengenänderung, die Änderung der fixen Kosten ergeben.
Diese ändern sich aber gerade nicht. Man kann eben nicht wie bei den variablen Kosten die Änderung
der Kosten errechnen, indem man die Stückkosten mit der Mengenänderung multipliziert. Tut man
dies doch, so hat man den Fehler der Fixkostenproportionalisierung begangen; man hat fixe Kosten,
die nicht proportional zur Menge sind, so behandelt wie variable Kosten, die proportional zur Menge
sind. Dies ist ein Problem der Vollkostenrechnung, in der alle Kosten, fixe und variable, auf das
einzelne Produkt umgelegt werden. Dagegen werden in der Teilkostenrechnung, beim Rechnen mit
Deckungsbeiträgen, nur die variablen Kosten auf das Produkt umgelegt. Deswegen gibt es hier das
Problem der Fixkostenproportionalisierung nicht.
-3-
582629546