1. WH
Werbung

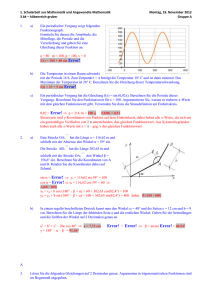
1. Lernzielkontrolle aus Mathematik und Angewandte Mathematik 3 ak – löffler 1. a) Mittwoch, 24. Oktober 2012 Gruppe A Der Funktionsgraph einer Sinusfunktion läuft wie in der Skizze angegeben. Berechnen Sie die Gleichung dieser Funktion. W(t) = 20 + 60 sin Error! 2. 3. 4. b) Ermitteln Sie die Periode der Funktion y = 50 sin(0,02094 x). Runden Sie die Periode dabei auf Ganze. Error! = 0,02094 p = 300 a) Ein periodischer Vorgang hat die Gleichung f(t) = 50 + 20 sin Error!. Geben Sie die Zeitpunkte dreier hintereinanderliegender Minima an. Wie hoch ist dieses Minimum? p = 12 v = 5 daher Minimum bei t = 5 + 3 · 3 = 14 und bei 26 und bei 38 und auch bei 2. Wert des Minimums = 30 b) Ein periodischer Vorgang hat ein Maximum bei x = 10 und das nächste Minimum tritt bei x = 14 auf. Die Funktion schwankt zwischen 5 und 7. Geben Sie die Gleichung dieses Vorgangs an. f(x) = 6 + sin Error! = 6 + sin Error! a) Von einem allgemeinen Dreieck kennt man die Winkel = 35° und γ = 88° und die Seite c = 15 cm. Berechnen Sie den fehlenden Winkel und die Seiten a und b. Error! = Error! a = Error! = 8,61 cm β = 180° – α – γ = 57° Error! = Error! b = Error! = 12,59 cm b) Berechnen Sie den Winkel, den die beiden Diagonalen eines Rechtecks mit den Seitenlängen 6 m und 4m einschließen. tan Error! = Error! α = 112,62° bzw. 67,38° a) Die Spitze S einer Stange mit der Höhe h erscheint von einem Beobachtungspunkt A aus unter dem Winkel = 5° und von B aus unter dem Winkel = 7°. Die beiden Beobachtungspunkte haben eine Entfernung von d = 85,43 m voneinander. Berechnen Sie die Höhe der h der Stange. ∠ ASB = 180° – α – (180° – β) = 2° = γ –– BS; = y Error! = Error! y = Error!= 213,35 m sin (β) = Error! h = y sin(β) = 26 m b) Der Sinuswert eines Winkels ist 0,5. Berechnen Sie mit dem Taschenrechner diesen Winkel in Grad. Überlegen Sie mit der Definition am Einheitskreis welcher Winkel noch den Sinuswert 0,5 hat und geben Sie diesen Winkel an. Fertigen Sie eine Skizze für diese Situation an. sin(α) = 0,5 α = arcsin(0,5) = 30° oder 180° – 30° = 150° 1. Lernzielkontrolle aus Mathematik und Angewandte Mathematik 3 ak – löffler 1. a) Mittwoch, 24. Oktober 2012 Gruppe B Der Funktionsgraph einer Sinusfunktion läuft wie in der Skizze angegeben. Berechnen Sie die Gleichung dieser Funktion. W(t) = 20 + 30 sin Error! 2. 3. 4. b) Ermitteln Sie die Periode der Funktion y = 50 sin(0,01257 x). Runden Sie die Periode dabei auf Ganze. Error! = 0,01257 p = 500 a) Ein periodischer Vorgang hat die Gleichung f(t) = 50 + 30 sin Error!. Geben Sie die Zeitpunkte dreier hintereinanderliegender Minima an. Wie hoch ist dieses Minimum? p = 12 v = 6 daher Minimum bei t = 6 + 3 · 3 = 15 und bei 27 und bei 39 und auch bei 3. Wert des Minimums = 20 b) Ein periodischer Vorgang hat ein Maximum bei x = 10 und das nächste Minimum tritt bei x = 14 auf. Die Funktion schwankt zwischen 7 und 9. Geben Sie die Gleichung dieses Vorgangs an. f(x) = 8 + sin Error! = 8 + sin Error! a) Von einem allgemeinen Dreieck kennt man die Winkel = 35° und γ = 88° und die Seite c = 30 cm. Berechnen Sie den fehlenden Winkel und die Seiten a und b. Error! = Error! a = Error! = 17,22 cm β = 180° – α – γ = 57° Error! = Error! b = Error! = 25,18 cm b) Berechnen Sie den Winkel, den die beiden Diagonalen eines Rechtecks mit den Seitenlängen 6 m und 5m einschließen. tan Error! = Error! α = 100,39° bzw. 79,61° a) Die Spitze S einer Stange mit der Höhe h erscheint von einem Beobachtungspunkt A aus unter dem Winkel = 5° und von B aus unter dem Winkel = 8°. Die beiden Beobachtungspunkte haben eine Entfernung von d = 69,03 m voneinander. Berechnen Sie die Höhe der h der Stange. ∠ ASB = 180° – α – (180° – β) = 3° = γ –– BS; = y Error! = Error! y = Error!= 114,96 m sin (β) = Error! h = y sin(β) = 16 m b) Der Kosinuswert eines Winkels ist 0,5. Berechnen Sie mit dem Taschenrechner diesen Winkel in Grad. Überlegen Sie mit der Definition am Einheitskreis welcher Winkel noch den Sinuswert 0,5 hat und geben Sie diesen Winkel an. Fertigen Sie eine Skizze für diese Situation an. cos(α) = 0,5 α = arccos(0,5) = 60° oder 360° – 60° = 300° 1. Lernzielkontrolle aus Mathematik und Angewandte Mathematik 3 ak – löffler 1. 2. 3. 4. Mittwoch, 24. Oktober 2012 Gruppe A a) Der Funktionsgraph einer Sinusfunktion läuft wie in der Skizze angegeben. Berechnen Sie die Gleichung dieser Funktion. b) Ermitteln Sie die Periode der Funktion y = 50 sin(0,02094 x). Runden Sie die Periode dabei auf Ganze. a) Ein periodischer Vorgang hat die Gleichung f(t) = 50 + 20 sin Error!. Geben Sie die Zeitpunkte dreier hintereinanderliegender Minima an. Wie hoch ist dieses Minimum? b) Ein periodischer Vorgang hat ein Maximum bei x = 10 und das nächste Minimum tritt bei x = 14 auf. Die Funktion schwankt zwischen 5 und 7. Geben Sie die Gleichung dieses Vorgangs an. a) Von einem allgemeinen Dreieck kennt man die Winkel = 35° und γ = 88° und die Seite c = 15 cm. Berechnen Sie den fehlenden Winkel und die Seiten a und b. b) Berechnen Sie den Winkel, den die beiden Diagonalen eines Rechtecks mit den Seitenlängen 6 m und 4m einschließen. a) Die Spitze S einer Stange mit der Höhe h erscheint von einem Beobachtungspunkt A aus unter dem Winkel = 5° und von B aus unter dem Winkel = 7°. Die beiden Beobachtungspunkte haben eine Entfernung von d = 85,43 m voneinander. Berechnen Sie die Höhe der h der Stange. b) Der Sinuswert eines Winkels ist 0,5. Berechnen Sie mit dem Taschenrechner diesen Winkel in Grad. Überlegen Sie mit der Definition am Einheitskreis welcher Winkel noch den Sinuswert 0,5 hat und geben Sie diesen Winkel an. Fertigen Sie eine Skizze für diese Situation an. 1. Lernzielkontrolle aus Mathematik und Angewandte Mathematik 3 ak – löffler 1. 2. 3. 4. Mittwoch, 24. Oktober 2012 Gruppe B a) Der Funktionsgraph einer Sinusfunktion läuft wie in der Skizze angegeben. Berechnen Sie die Gleichung dieser Funktion. b) Ermitteln Sie die Periode der Funktion y = 50 sin(0,01257 x). Runden Sie die Periode dabei auf Ganze. a) Ein periodischer Vorgang hat die Gleichung f(t) = 50 + 30 sin Error!. Geben Sie die Zeitpunkte dreier hintereinanderliegender Minima an. Wie hoch ist dieses Minimum? b) Ein periodischer Vorgang hat ein Maximum bei x = 10 und das nächste Minimum tritt bei x = 14 auf. Die Funktion schwankt zwischen 7 und 9. Geben Sie die Gleichung dieses Vorgangs an. a) Von einem allgemeinen Dreieck kennt man die Winkel = 35° und γ = 88° und die Seite c = 30 cm. Berechnen Sie den fehlenden Winkel und die Seiten a und b. b) Berechnen Sie den Winkel, den die beiden Diagonalen eines Rechtecks mit den Seitenlängen 6 m und 5m einschließen. a) Die Spitze S einer Stange mit der Höhe h erscheint von einem Beobachtungspunkt A aus unter dem Winkel = 5° und von B aus unter dem Winkel = 8°. Die beiden Beobachtungspunkte haben eine Entfernung von d = 69,03 m voneinander. Berechnen Sie die Höhe der h der Stange. b) Der Kosinuswert eines Winkels ist 0,5. Berechnen Sie mit dem Taschenrechner diesen Winkel in Grad. Überlegen Sie mit der Definition am Einheitskreis welcher Winkel noch den Sinuswert 0,5 hat und geben Sie diesen Winkel an. Fertigen Sie eine Skizze für diese Situation an.