1. SA

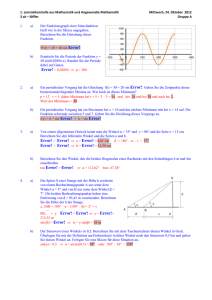
1. Schularbeit aus Mathematik und Angewandte Mathematik
3 bk – höbenreich-gruber
1.
a)
Montag, 19. November 2012
Gruppe A
Ein periodischer Vorgang zeigt folgenden
Funktionsgraph:
Ermitteln Sie daraus die Amplitude, die
Mittellage, die Periode und die
Verschiebung und geben Sie eine
Gleichung dieser Funktion an.
a = 80 m = 100, p = 100, v = 0
f(x) = 100 + 80 sin Error!
b)
Die Temperatur in einem Raum schwankt
mit der Periode 16 h. Zum Zeitpunkt t = 4 beträgt die Temperatur 18° C und ist dann minimal. Das
Maximum der Temperatur ist 28° C. Berechnen Sie die Gleichung dieser Temperaturschwankung.
f(t) = 23 + 5 sin Error!
c)
Ein periodischer Vorgang hat die Gleichung f(x) = sin (0,02x). Berechnen Sie die Periode dieses
Vorgangs. Berechnen Sie den Funktionswert für x = 100. Argumentieren Sie, warum es mehrere x-Werte
mit dem gleichen Funktionswert gibt. Verwenden Sie dazu die Sinusdefinition am Einheitskreis.
0,02 = Error!  p = 314,16 = 100 
f(100) = 0,91
Sinuswerte sind y-Koordinaten von Punkten auf dem Einheitskreis, daher haben alle x-Werte, die sich um
ein ganzzahliges Vielfaches von 2  unterscheiden, den gleichen Funktionswert. Aus Symmetriegründen
haben auch alle x-Werte mit x =  – geg. x den gleichen Funktionswert.
2.
a)
––
Eine Strecke OA; hat die Länge a = 116,62 m und
schließt mit der Abszisse den Winkel α = 59° ein.
––
Die Strecke AB; hat die Länge 302,65 m und
––
schließt mit der Strecke OA;
den Winkel β =
156,6° ein. Berechnen Sie die Koordinaten von A
und B. Runden Sie die Koordinaten dabei auf
Zehntel.
sin  = Error!  ya = 116,62 sin 59° = 100
cos  = Error!  xa = 116,62 cos 59° = 60 
A(60 / 100)
xb = xa + b cos (180° –  + ) = 60 + 302,65 cos(82,4°) = 100
yb = ya + b sin (180° –  + ) = 100 + 302,65 sin(82,4°) = 400 daher B (100 / 400)
b)
In einem regulär beschrifteten Dreieck kennt man den Winkel  = 40° und die Seiten c = 12 cm und b = 9
cm. Berechnen Sie die Länge der fehlenden Seite a und die restlichen Winkel. Geben Sie die Seitenlängen
und die Größen der Winkel auf 2 Dezimalen genau an
a2 = b2 + c2 – 2bc cos 40°  a = 7,72 cm
γ = 180° –  –  = 91,46°
Error! = Error!   = arcsin Error! = 48,54°
A
3.
Lösen Sie die folgenden Gleichungen auf 2 Dezimalen genau. Argumenten in trigonometrischen Funktionen sind
im Bogenmaß angegeben.
a)
arccos(3x) + 1 = 1,2046
arccos(3x) + 1 = 1,45
b)
4log
 arccos(3x) = 0,45  3x = 0,9  x = 0,3
(x + 4) = 1,9037
x + 4 = 41,9037 = 14  x = 10
4.
Lösen Sie die folgenden Gleichungen nach x:
a)
ln ( ax) = b
b)
ax = eb  ax = e2b  x = Error!
3;a + b sin(x) = c
a + b sin(x) = c3  b sin(x) = c3 – a  sin(x) = Error!  x = arcsin Error!
1. Schularbeit aus Mathematik und Angewandte Mathematik
3 bk – höbenreich-gruber
1.
a)
Montag, 19. November 2012
Gruppe B
Ein periodischer Vorgang zeigt
folgenden Funktionsgraph:
Ermitteln Sie daraus die
Amplitude, die Mittellage, die
Periode und die Verschiebung und
geben Sie eine Gleichung dieser
Funktion an.
a = 16 m = 20, p = 100, v = 0
f(x) = 20 + 16 sin Error!
b)
Die Temperatur in einem Raum
schwankt mit der Periode 20 h. Zum Zeitpunkt t = 4 beträgt die Temperatur 18° C und ist dann minimal.
Das Maximum der Temperatur ist 38° C. Berechnen Sie die Gleichung dieser Temperaturschwankung.
f(t) = 28 + 10 sin Error!
c)
Ein periodischer Vorgang hat die Gleichung f(x) = sin (0,2x). Berechnen Sie die Periode dieses Vorgangs.
Berechnen Sie den Funktionswert für x = 5. Argumentieren Sie, warum es mehrere x-Werte mit dem
gleichen Funktionswert gibt. Verwenden Sie dazu die Sinusdefinition am Einheitskreis.
0,2 = Error!  p = 31,416 = 10  f(5) = 0,84
Sinuswerte sind y-Koordinaten von Punkten auf dem Einheitskreis, daher haben alle x-Werte, die sich um
ein ganzzahliges Vielfaches von 2  unterscheiden, den gleichen Funktionswert. Aus Symmetriegründen
haben auch alle x-Werte mit x =  – geg. x den gleichen Funktionswert.
2.
a)
––
Eine Strecke OA; hat die Länge a = 161,55 m und
schließt mit der Abszisse den Winkel α = 68,2° ein.
––
Die Strecke AB; hat die Länge 250,8 m und
––
schließt mit der Strecke OA;
den Winkel β =
162,8° ein. Berechnen Sie die Koordinaten von A
und B. Runden Sie die Koordinaten dabei auf
Zehntel.
sin  = Error!  ya = 161,55 sin 68,2° = 150
cos  = Error!  xa = 161,55 cos 68,2° = 60 
A(60 / 150)
xb = xa + b cos (180° –  + ) = 60 + 250,8 cos(85,4°) = 80
yb = ya + b sin (180° –  + ) = 150 + 250,8 sin(85,4°) = 400 daher B (80 / 400)
b)
In einem regulär beschrifteten Dreieck kennt man den Winkel  = 40° und die Seiten c = 60 cm und b =
45 cm. Berechnen Sie die Länge der fehlenden Seite a und die restlichen Winkel. Geben Sie die
Seitenlängen und die Größen der Winkel auf 1 Dezimale genau an
a2 = b2 + c2 – 2bc cos 40°  a = 38,6 cm
Error! = Error!   = arcsin Error! = 48,54°
γ = 180° –  –  = 91,46°
B
3.
Lösen Sie die folgenden Gleichungen auf 2 Dezimalen genau. Argumenten in trigonometrischen Funktionen sind
im Bogenmaß angegeben.
a)
arccos(2x) + 3 = 1,7321
arccos(2x) + 3 = 3
b)
6log
 arccos(2x) = 0  2x = 1  x = 0,5
(x + 5) = 1,7965
x + 5 = 61,7965 = 25  x = 20
4.
Lösen Sie die folgenden Gleichungen nach x:
a)
ln (a x) = b
b)
a x = eb  x = Error!
3;b + a sin(x) = c
b + a sin(x) = c3  a sin(x) = c3 – b  sin(x) = Error!  x = arcsin Error!
1. Schularbeit aus Mathematik und Angewandte Mathematik
3 bk – höbenreich-gruber
1.
2.
a)
Ein periodischer Vorgang zeigt
folgenden Funktionsgraph:
Ermitteln Sie daraus die Amplitude,
die Mittellage, die Periode und die
Verschiebung und geben Sie eine
Gleichung dieser Funktion an.
b)
Die Temperatur in einem Raum
schwankt mit der Periode 16 h.
Zum Zeitpunkt t = 4 beträgt die
Temperatur 18° C und ist dann minimal. Das Maximum der Temperatur ist 28° C.
Berechnen Sie die Gleichung dieser Temperaturschwankung.
c)
Ein periodischer Vorgang hat die Gleichung f(x) = sin (0,02x). Berechnen Sie die
Periode dieses Vorgangs. Berechnen Sie den Funktionswert für x = 100.
Argumentieren Sie, warum es mehrere x-Werte mit dem gleichen Funktionswert gibt.
Verwenden Sie dazu die Sinusdefinition am Einheitskreis.
a)
b)
3.
––
Eine Strecke OA; hat die Länge a =
116,62 m und schließt mit der Abszisse den
––
Winkel α = 59° ein. Die Strecke AB; hat
die Länge 302,65 m und schließt mit der
––
Strecke OA;
den Winkel β = 156,6° ein.
Berechnen Sie die Koordinaten von A und
B. Runden Sie die Koordinaten dabei auf
Zehntel.
In einem regulär beschrifteten Dreieck
kennt man den Winkel  = 40° und die Seiten c = 12 cm und b = 9 cm. Berechnen Sie
die Länge der fehlenden Seite a und die restlichen Winkel. Geben Sie die Seitenlängen
und die Größen der Winkel auf 2 Dezimalen genau an
Lösen Sie die folgenden Gleichungen auf 2 Dezimalen genau. Argumenten in
trigonometrischen Funktionen sind im Bogenmaß angegeben.
a)
b)
4.
Montag, 19. November 2012
Gruppe A
arccos(3x) + 1 = 1,2046
4log
(x + 4) = 1,9037
Lösen Sie die folgenden Gleichungen nach x:
a)
ln ( ax) = b
b)
3;a + b sin(x) = c
1. Schularbeit aus Mathematik und Angewandte Mathematik
3 bk – höbenreich-gruber
1.
2.
a)
Ein periodischer Vorgang
zeigt folgenden
Funktionsgraph:
Ermitteln Sie daraus die
Amplitude, die Mittellage,
die Periode und die
Verschiebung und geben Sie
eine Gleichung dieser
Funktion an.
b)
Die Temperatur in einem
Raum schwankt mit der
Periode 20 h. Zum Zeitpunkt t = 4 beträgt die Temperatur 18° C und ist dann minimal.
Das Maximum der Temperatur ist 38° C. Berechnen Sie die Gleichung dieser
Temperaturschwankung.
c)
Ein periodischer Vorgang hat die Gleichung f(x) = sin (0,2x). Berechnen Sie die Periode
dieses Vorgangs. Berechnen Sie den Funktionswert für x = 5. Argumentieren Sie,
warum es mehrere x-Werte mit dem gleichen Funktionswert gibt. Verwenden Sie dazu
die Sinusdefinition am Einheitskreis.
a)
b)
3.
––
Eine Strecke OA; hat die Länge a =
161,55 m und schließt mit der Abszisse den
––
Winkel α = 68,2° ein. Die Strecke AB;
hat die Länge 250,8 m und schließt mit der
––
Strecke OA;
den Winkel β = 162,8° ein.
Berechnen Sie die Koordinaten von A und
B. Runden Sie die Koordinaten dabei auf
Zehntel.
In einem regulär beschrifteten Dreieck
kennt man den Winkel  = 40° und die Seiten c = 60 cm und b = 45 cm. Berechnen Sie
die Länge der fehlenden Seite a und die restlichen Winkel. Geben Sie die Seitenlängen
und die Größen der Winkel auf 1 Dezimale genau an
Lösen Sie die folgenden Gleichungen auf 2 Dezimalen genau. Argumenten in
trigonometrischen Funktionen sind im Bogenmaß angegeben.
a)
b)
4.
Montag, 19. November 2012
Gruppe B
arccos(2x) + 3 = 1,7321
6log
(x + 5) = 1,7965
Lösen Sie die folgenden Gleichungen nach x:
a)
ln (a x) = b
b)
3;b + a sin(x) = c