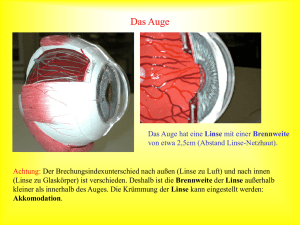
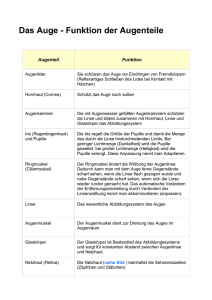
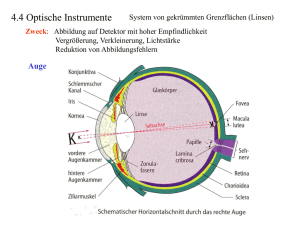
8.2.4 Linsen

1
Vorlesung Experimentalphysik II am 21.6.1999
J. Ihringer
8.2.4 Linsen
Dem Brechungsgesetz folgt der Strahlengang in Linsen, die parallel zur optischen Achse
einfallende Strahlen auf einen Punkt, den Fokus, ablenken.
Konvexlinse
Konkavlinse
f
1 1
1
 (n  1)    
f
 r1 r2 
D
1
f
r1 , r2
N
f
Brennweite f
Brechkraft,
ihre Einheit ist 1 Dioptrie=1 m 1
Krümmungsradien der die Linse
begrenzenden Kugelflächen
Brechungsindex des Linsenmaterials
Abbildung 1 Konvex- und Konkavlinse.
Versuch 1 Radar-Linse: Eine fokussierende Linse für Radarstrahlen entsteht aus Scheiben
unterschiedlichen Durchmessers mit einer homogenen Metall Beschichtung (Reißnägel, die in
etwa gleicher Dichte aufgebracht sind).
Abbildung 2 Schema der Linse für Radarstrahlen (   3,2 cm) : Homogen mit Reißnägeln
versehene Styroporplatten, ca. 1 Reißnagel/cm2.
2
Zur eindeutigen Konstruktion von Strahlengängen wählt man zwei Strahlen, die den
folgenden Bedingungen genügen:
f
Umgekehrt:
Brennebene
Parallel einfallende Strahlen verlaufen nach dem Durchqueren der Linse durch
einen Punkt in der Brennebene.
Strahlen, die von einem Punkt in der Brennebene ausgehen, verlaufen nach
dem Durchqueren der Linse parallel.
Strahlen durch die Mitte der Linse verlaufen ungebrochen.
Abbildung 3 Regeln zur Konstruktion von Strahlengängen
8.2.5 Abbildung im Auge
Viele optische Instrumente, Brille, Lupe, Mikroskop und Fernrohr, dienen der Verbesserung
der Abbildung durch das Auge. Das Auge ist selbst ein optisches System. Zunächst fragen
wir, welche Intensitätsverteilung vor unserer Linse ansteht. Um den Überblick zu wahren,
ersetzt man die Sicht auf irgendeine belebte Szene oder Landschaft durch den Blick auf einen
beleuchteten Spalt in sonst dunkler Umgebung. Zur weiteren Vereinfachung beleuchtet man
statt mit weißem, in unregelmäßig langen Wellenzügen unterschiedlicher Frequenz
ausgesendetem Sonnenlicht mit einer monochromatischen, harmonischen Welle eines Lasers.
An die Stelle des Auges stellt man schließlich einen Schirm und beobachtet die
Intensitätsverteilung darauf, die qualitativ in der Abbildung zum Huygens-Fresnelschen
Prinzip gezeigt ist.
Wird der beleuchtete Spalt mit dem Auge beobachtet, dann steht an Stelle des Schirms die
Linse, die Pupille blendet die Randstrahlen aus. Auf der Vorderseite der Linse steht das
Beugungsbild des Spalts, das durch die Linse in das reale Bild des Spalts auf der Netzhaut
verwandelt wird. Es ist offensichtlich, daß sowohl die Entstehung des Beugungsbilds als auch
die Bildentstehung des Spalts auf der Netzhaut nicht mit Strahlenoptik zu verstehen ist. Auch
hier hilft das Wellenbild des Huygens-Fresnelschen Prinzips: Die an der Linse anliegende
Intensitätsverteilung regt elektrische Dipole im Auge zur Schwingung an. Die von ihnen
ausgesendeten Kugelwellen überlagern sich so, daß bei geeigneter geometrischer Anordnung
der Dipole in Hornhaut, Linse und Glaskörpers und geeigneter Positionierung der Netzhaut
auf letzerer ein scharfes Bild des Gegenstands erscheint.
Es wird bei dieser Betrachtung klar, daß zum Sehen zwei unterschiedliche Effekte beitragen:
Der erste ist die Beugung des Lichts an den Objekten. Die Beugung ist robust und von
geometrischen Gegebenheiten unabhängig: Immer dann, wenn ein Objekt beleuchtet wird,
entsteht ein Beugungsbild. Der zweite Effekt verwandelt das Beugungsbild vor der Linse in
ein Abbild des Objekts auf der Netzhaut. Dieser Vorgang ist subtiler, es müssen im Auge
Formen und Abstände der optischen Komponenten aufeinander abgestimmt sein, um ein
scharfes Bild zu erhalten.
3
Bild des
beleuchtete
n Spalts
Pupille
mit Linse
Spaltbreite a
Netzhaut
 Pr imärstrahl
Breite des Maximums ~ 1 a
Abbildung 4 Beugungsbild vor der Linse und Bild auf der Netzhaut: Das Auge erzeugt aus
dem Beugungsbild vor der Linse das Bild des Spalts auf der Netzhaut.
Wenn ein Objekt über die ganze Öffnung der Linse eine konstante Intensität erzeugt, dann
sieht man nur einen hellen Punkt. Das Objekt ist zu klein, um aufgelöst zu werden. Zu klein
heißt, daß die Winkel, unter denen die vom Objekt ausgehenden Wellenfelder auf die Öffnung
des Auges treffen, um weniger als 1 / 120 0 , der Auflösungsgrenze des Auges, gegeneinander
geneigt sind. Diese Begrenzung tritt in Erscheinung, wenn zwei leuchtende Punkte beobachtet
werden, die jeweils eine Kugelwelle aussenden, z. B. zwei Sterne am nächtlichen Himmel.
Beide Kugelwellen erscheinen vor der Linse als ebene Welle. Die Sterne werden nur dann
getrennt wahrgenommen, wenn die Einfallswinkel ihrer Wellenfelder mehr als 1 / 120 0
getrennt liegen. Der Winkel zwischen den Sternen muß also, mit bloßem Auge beobachtet,
mindestens 1 / 120 0 betragen.
Ein Wellenfeld mit nur einer Richtung wird aber auch bei der Beugung beobachtet, wenn die
einzelnen Ordnungen so ausgedehnt sind, daß nur eine von ihnen auf die Pupille trifft. Man
betrachte z. B. die Abbildung oben mit dem Spalt und dem Auge. Wird der Spalt kleiner,
dann fällt nur noch das zentrale Maximum mit nahezu konstanter Intensität in die Linse. Auch
dann wird das Objekt nur als Lichtquelle gesehen, es ist zu klein, um genaueres zu erkennen.
Der von einer einzigen Welle erzeugte Punkt auf der Netzhaut zeigt zwar keine Information
über das Objekt, er ist aber das Beugungsbild der Pupille. Man versteht das, wenn man die
Pupille als Blende sieht, die im Licht der einfallenden ebenen Welle steht. Ihr Beugungsbild
wird auf der Netzhaut abgebildet. Der kleinste Lichtpunkt auf der Netzhaut wird von einer
einzigen ebenen Welle erzeugt, er ist das zentrale Maximum des Beugungsbilds der Pupille.
Die Evolution hat die Größe der Zäpfchen gerade dem Durchmesser dieses zentralen
Maximums angepaßt. Eine feinere Unterteilung der Netzhaut würde nur bei gleichzeitiger
Vergrößerung der Pupille die Auflösung des Systems verbessern.
4
Abbildung 5 Schema des Auges. Der mittlere Abstand der Zäpfchen ist dem
Beugungsscheibchen der Pupille angepaßt (Quelle: Meyers Enzyklopädisches Lexikon)
In der folgenden Tabelle sind die wichtigsten optischen Eigenschaften des Auges
zusammengefaßt. Herausragend ist der weite Bereich der Leuchtdichte, das ist der Bereich der
zwischen der Empfindung völliger Dunkelheit und blendender Helligkeit, in dem das Auge
Abbildungen liefert. Neben den physikalischen Daten ist das Nervensystem in der Retina
erwähnenswert, das durch spezielle Verknüpfungen einige Gehirnfunktionen zur
Informationsaufbereitung schon im Auge ausführt.
5
Optische Daten zum menschlichen Auge:
Verhältnis der Leuchtdichte an der unteren
Grenze des Erkennens zur höchsten
etwa 1 : 1012
Leuchtdichte vor der Blendung:
Auflösungsvermögen: Kleinster Winkel, unter
1 0
dem zwei Punkte noch getrennt wahrnehmbar ~
120
sind:
Anzahl der Sehzellen
125  10 6
1
166000
Höchste Dichte der Sehzellen
mm 2
1,2 m
Radius der Sehzellen
Horizontaler Sehwinkel
Etwa 110° bis 120°
Pupillendurchmesser, regelbar
1-8 mm
Gesamte Brechkraft des Auges
58 Dioptrien
Verteilt sich auf:
Linse
13 Dioptrien
Hornhaut, Kammerwasser und Glaskörper 45 Dioptrien
Tabelle 1 Optische Eigenschaften des menschlichen Auges
8.2.6 Abbildung durch optische Instrumente
Ein Gegenstand wird durch eine Linse optisch „abgebildet“. Im Bild der Strahlenoptik kann
die Vergrößerung mit Hilfe des Strahlensatzes leicht bestimmt werden, wenn man die
Abbildung mit zwei Strahlen charakterisiert. Man wählt, entsprechend den o. g. Regeln, einen
parallel zur Linsenachse einfallenden Strahl, der durch den Brennpunkt der Linse gebrochen
wird, und einen Strahl durch die Linsenmitte, der die Linse ungebrochen durchquert. Bei der
folgenden Formulierung denke man sich das Bild des Gegenstands auf einen Schirm projiziert
(„reelles Bild“).
f
Gegensta
nd, Größe
G
f
Bild,
Größe B
g
b
1 1 1
 
f b g
 
b g

B G
Abbildungsgleichung
Abbildungsmaßstab
6
Folgt aus:
g f
f

G
B
Strahlensatz für den Strahl
durch den Fokus links
b
g

B G
Strahlensatz für den Strahl
durch die Mitte
Tabelle 2 Abbildungsgleichung und Abbildungsmaßstab. Der dritte (z. B. der unterste) Strahl
ist zur Vollständigkeit eingezeichnet, er ist zur Konstruktion nicht notwendig.
Wenn man das Bild nicht auf dem Schirm abbildet, sondern den Gegenstand durch das
optische Gerät hindurch mit dem Auge beobachtet, dann enthält das optische System auch
noch die Linse des Auges. Die Vergrößerung eines optischen Geräts ist dann als Verhältnis
der Tangens Werte der „Sehwinkel“ definiert. Das sind zwei Winkel, unter denen man einen
Punkt mit und ohne Instrument erblickt. In astronomischen Fernrohren ist der Punkt das
Objekt selbst, z. B. der leuchtende Stern. In Lupen und Mikroskopen befinde sich der Punkt
am beobachteten Gegenstand, der zur Beobachtung ohne Instrument in die Bezugssehweite
l 0  25cm vor das Auge gestellt wird.
Die Bezugssehweite steht für die kleinste Entfernung, aus der bei normaler Akkomodation
noch scharf gesehen wird.

0
l 0  25cm
V 
tan 


tan  0  0

0
l 0  25cm :
Vergrößerung
Sehwinkel eines Punktes mit Instrument.
Sehwinkel eines Punktes ohne Instrument.
Bei Lupen und Mikroskopen befinde sich der
Punkt an einem Gegenstand, der in
Bezugssehweite aufgestellt ist.
Definition der Bezugssehweite: Standard
Entfernung eines Gegenstandes von einem auf
Nähe akkommodierten Auge.
Tabelle 3 Definition der Vergrößerung und des Sehwinkels.
7
8.2.6.1
Die Lupe
Mit einer Lupe erscheinen kleine Gegenstände unter einem größeren Sehwinkel, also
vergrößert. Bringt man den Gegenstand in die Brennebene der Linse, dann gilt:
l0
G
0
Sehwinkel ohne Lupe,
Gegenstand im Abstand
l 0  25cm , die Länge
des Pfeils sei G.
f
f
Sehwinkel mit Lupe
  0
VLupe 
G
G f l0
tan 


tan  0 G l0
f
Vergrößerung einer
Lupe
Tabelle 4 Strahlengang und Vergrößerung einer Lupe
8.2.6.2
Das Keplersche und Galileische astronomische Fernrohr
Die Beobachtung des Himmels mit astronomischen Fernrohren dient der Bestimmung von
Sternorten. Das heißt, es interessiert nicht das Aussehen der Oberfläche eines Sterns, sondern
man möchte die Koordinaten seines „Punktes“ am Himmel bestimmen oder man möchte
wissen, ob ein mit bloßem Auge als Punkt am Himmel erscheinender „Stern“ vielleicht eine
Ansammlung von zwei oder mehreren Sternen ist. Um Sterne getrennt wahrzunehmen, muß
sich ihr Sehwinkel um einen kleinsten, letztlich durch die Auflösung der Netzhaut im Auge
gegebenen Winkel unterscheiden, der beim Menschen 1/120 ° beträgt.
Im Gegensatz zur zuvor besprochenen Lupe nimmt man in diesen Instrumenten an, daß die
von einem weit entfernten Gegenstand die Strahlen parallel zueinander in das Objektiv
einfallen. Nach den Eigenschaften der Linse beobachtet man deshalb einen Stern als
leuchtenden Punkt in der Fokal Ebene. Dieser Punkt zeigt aber nur die Beugungsfigur eines
im Weg des parallelen Strahlenbündels befindlichen Gegenstandes, das ist die Öffnung des
Fernrohrs. Man kann deshalb keine Details von der Oberfläche der Quelle, also des Sterns,
erkennen. Die Eigenschaften der Beugung werden später im Wellenbild detailliert dargelegt,
hier sei aber schon verraten, daß ein Bündel parallel einfallender Strahlen keine Information
über die Struktur der Quelle enthält, es steht für eine einzige Beugungsordnung von der
Quelle. Für die Abbildung benötigt man aber mindestens zwei, besser mehrere Ordnungen.
8
Die Beobachtung eines einzigen Bündels paralleler Strahlen ist ausreichend, wenn man sich
damit begnügt, die Richtung des einfallenden Lichtes zu registrieren.
2 0
Tabelle 5 Links: Schema der Netzhaut mit dem Bild der beiden rechts beobachteten Sterne.
Das Karo steht für das Raster der Netzhaut. Liegt das Bild beider Sterne in einem
Rasterpunkt, dann sieht man die Sterne nicht mehr als getrennte Objekte.
Im Rahmen der Strahlenoptik ist deshalb nur die Änderung des Sehwinkel bei Nutzung des
Instruments von Interesse. Die Vergrößerung des Instruments wird aus den Sehwinkeln für
den weit entfernten Gegenstand mit und ohne Fernrohr definiert.
Das Keplersche Fernrohr enthält als Objektiv und Okular zwei konvexe Linsen
unterschiedlicher Brennweiten, das Objekt wird dadurch „auf dem Kopf stehend“ gesehen. Im
Galileischen Fernrohr wird durch eine konkave Linse als Okular erreicht, daß das Objekt
„aufrecht“ erscheint. Betrachtet man mit dem Fernrohr irdische Gegenstände, z. B. einen
Kirchturm, dann treten anstelle der Sterne Punkte des Objekts. Man profitiert auch dann von
der Vergrößerung des Sehwinkels zwischen benachbarten Punkten.
f1
f2
f1
f2
B
0

f
tan 
 1
tan  0
f2
B
tan  
f2
B
tan  0 
f1
VFernrohr 
Vergrößerung des Fernrohrs
Winkel am Okular
Winkel am Objektiv
Tabelle 6 Strahlengang und Vergrößerung im Keplerschen Fernrohr. Der gleiche Ausdruck
folgt für das Galileische Fernrohr.
9
8.2.6.3
Das Mikroskop
Wie bei der Lupe fällt ein divergentes Strahlenbündel vom Objekt G in das Objektiv, dieses
bildet das Objekt in der Bildebene des Objektivs als reelles Bild B ab. Man könnte das
vergrößerte Objekt dort auf einem Schirm abbilden und dieses Abbild dann z. B. mit einer
Lupe nochmals vergrößert betrachten. Das macht man im Mikroskop tatsächlich, nur
verzichtet man auf den Schirm, der nicht nötig ist.
Sehwinkel ohne
Mikroskop,
Gegenstand im
Bezugsabstand
l 0  25cm , der
Pfeil zeige den
Gegenstand G.
l0
0
b
t
f2
g
f1
f1
f2
B
G

Okular als Lupe
Abbildung durch das Objektiv
Tabelle 7 Oben: Sehwinkel für einen Gegenstand ohne Instrument in Bezugssehweite, unten:
Sehwinkel und Strahlengang im Mikroskop
Zur Berechnung der Vergrößerung wird der Sehwinkel  , unter dem der Gegenstand bei
Beobachtung durch das Instrument erscheint, mit dem Sehwinkel  0 verglichen, unter dem
der in Bezugssehweite l 0  25cm befindliche Gegenstand mit bloßem Auge erscheint.
Die Vergrößerung steigt mit abnehmender Brennweite der Linsen. Man kann bis zu etwa
1000-fach vergrößern, bei höheren Vergrößerungen treten Beugungseffekte in den
Vordergrund: Die Auflösungsgrenze ist erreicht, wenn noch mindestens zwei unterschiedlich
gerichtete Parallelstrahlbündel in das Auge fallen. Ist nur noch eines übrig, dann wird –
10
ähnlich zur Beobachtung eines Sterns im Fernrohr- nur noch der zentrale Strahl des
Beugungsbildes beobachtet: Es wird zwar hell, aber es ist keine Struktur erkennbar. Die
Beugungseffekte werden im Bild der Wellenoptik verständlich.
t  l0
tan 

  Objektiv  VOkular
tan  0
f1  f 2
l
VOkular  0
f2
b
t
 Objektiv  
g f1
Folgt nach Einsetzen von:
G
tan  0 
l0
B
tan  
f2
B b

G g
1 1 1
 
f1 b g
VMikroskop 
b b  f1
t


g
f1
f1
VMikroskop 
Vergrößerung im Mikroskop
Vergrößerung des Okulars
(Lupe)
Vergrößerung des Objektivs
(einzelne Linse)
Sehwinkel des Gegenstands in
der Bezugssehweite
Sehwinkel durch das Okular
Strahlensatz für das Objektiv
Abbildungsgleichung für das
Objektiv, deshalb gilt
wegen b  t  f1 .
B  l0
b  l0
t  l0
tan 



tan  0 G  f 2 g  f 2
f1  f 2
Tabelle 8 Vergrößerung im Mikroskop
8.2.7 Linsenfehler
8.2.7.1
Sphärische Aberration
Bei sphärischen Linsen haben Randstrahlen eine geringere Brennweite als achsennahe
Strahlen. Die Abbildung wird verbessert, wenn man das Strahlenbündel durch Blenden
einschränkt.
f
Abbildung 6 Sphärische Aberration und ihre Korrektur durch Abblenden
f
11
8.2.7.2
Chromatische Aberration
Unterschiedliche Farben werden von Glas unterschiedlich stark gebrochen. Die Abhängigkeit
der Brechzahl eines Stoffes von der Wellenlänge des Lichtes bezeichnet man als Dispersion.
Die Brennweite für blaues Licht ist kürzer als die von rotem.
blau
rot
f
Man gleicht diesen Fehler durch „Achromat“ Linsen aus, dieses sind Kombinationen von
Linsen aus Gläsern unterschiedlicher Brechkraft und Dispersion, z.B. aus bleihaltigem
Flintglas (n=1,613) und bleifreiem Kronglas (n=1,510).
Versuch 2 Farbfehler der Linse. Licht hinter einem Filter, der für rot und blau durchlässig ist,
wird auf blau (rot) fokussiert. a) Man erkennt den roten (blauen) Hof um den Fokus. b) Mit
einer Achromat Linse ist das Bild scharf und ohne Farbrand.
Versuch 3 Dispersion des Prismas und Achromat Prisma. Ein Prisma aus Flintglas wird von
der Hälfte eines weißen Strahles durchquert, die andere Hälfte streicht geradeaus über das
Prisma hinweg. a) Der das Prisma durchquerende Strahl wird abgelenkt und spektral zerlegt,
der andere bleibt weiß. b) Mit einer Linse wird der regenbogenfarbige Strahl zu einem weißen
vereint, die Summe aller Farben ist weiß. c) Jetzt wird in voller Strahlhöhe ein
Kronglasprisma addiert: Der zuvor weiße Strahl wird bunt, der bunte zu weiß „korrigiert“.
8.2.7.3
Astigmatismus
Eine Zylinderlinse fokussiert nur in einer Richtung. Aus einem parallel einfallenden
Strahlenbündel wird deshalb kein Punkt, sondern eine Linie parallel zur Zylinderachse. Mit
einer zweiten dazu senkrecht stehenden Zylinderlinse kann dieser Fehler korrigiert werden.
Auch bei sphärischen Linsen gibt es astigmatische Verzeichnungen, wenn die Strahlen sehr
schräg zur optischen Achse geneigt in die Linse fallen. Man bezeichnet diesen Effekt als
„Astigmatismus schiefer Bündel“.
Versuch 4 Astigmatismus. a) Ein Netz wird mit einer Zylinderlinse abgebildet und stark
verzeichnet. b) Mit einer zweiten, dazu senkrecht stehenden Linse wird der Fehler (zumindest
in Nähe der Strahlachse) korrigiert.
12
8.2.8 Komplementärfarben
Young (1807) und Helmholtz (1852) erkannten, daß man unter der Annahme, das Auge habe
drei Farbrezeptoren für Rot, Grün und Blau (R, G, B), die Farbempfindung für alle Farben
erklären kann. Dieses Modell ist der Ausgangspunkt für das unten dargestellte Farbdreieck,
das von R, G, B aufgespannt wird. Die Werte auf der Abszisse geben den Rot Anteil, die auf
der Ordinate den Grün Beitrag, der Blau Anteil ist der Abstand von der Hypotenuse.
Anteil
von
Grün
Anteil von
Blau = Länge
des Lots auf
diese
„Hypotenuse“
 2
Anteil von
rot
Abbildung 7 Darstellung der sichtbaren Farbarten. Zusätzlich ist grau die „Hypotenuse“
eingezeichnet. Die Koordinaten eines jeden Punktes und sein Abstand von der Hypotenuse
zeigt den RGB Anteil der zum Punkt gehörenden Farbe. Am Rande der Kurve sind die
Wellenlängen eingetragen (Quelle: Meyers Enzyklopädisches Lexikon).
13
Mischungen zwischen zwei Farben liegen auf der Verbindungslinie zwischen den
entsprechenden Farbpunkten. Liegt weiß auf dieser Linie, dann sind die beiden Farben
„komplementär“ zueinander.
Versuch 5 Aus zwei Lichtquellen wird blaues und gelbes Licht überlagert, ebenso rotes und
grünes. Bei entsprechender Intensität erscheint die Addition der Farbpaare (annähernd)
weiß.
8.3 Die Polarisation von Licht
8.3.4 Linear polarisiertes Licht
Das Licht ist eine elektromagnetische Welle, die von den schwingenden Elektronen der
Atome ausgesandt wird. Nimmt man an, nur ein einziges Elektron schwinge in einer Ebene,

dann breitet sich das elektrische Feld E in der Schwingungsebene des Dipols aus, das


Magnetfeld B steht senkrecht dazu. Die maximale Intensität wird in Richtung s senkrecht

zum Dipol abgestrahlt, in Richtung der Dipolachse ist die Intensität null. Ist s die


Ausbreitungsrichtung, dann bezeichnet man die von B und s aufgespannte Ebene als die
Polarisationsebene der Welle. Die vom Dipol abgestrahlte Welle ist linear polarisiert.
Dipol
Polarisationsebene

E

s

B
Abbildung 8 Definition der Polarisationsebene
Natürliches Licht wird von vielen in beliebigen Richtungen schwingenden Elektronen
erzeugt, es ist deshalb unpolarisiert.
Geräte, die nur in einer Richtung polarisiertes Licht durchlassen, heißen Polarisatoren. Mit
Analysatoren kann man die Polarisationsrichtung erkennen. Letztere sind um die
Ausbreitungsrichtung drehbar. Ist der Analysator um den Winkel  gegenüber der
Polarisationsebene verdreht, dann ist die Feldstärke der durchgelassenen Strahlung
E  EP  cos
Wegen I ~ E gilt
I ~ cos 2 
14
Vom Analysator
durchgelassene
Komponente

E Feld des
polarisierten
Lichts

Analysatorebene
Abbildung 9 Intensität nach dem Analysator
8.3.4.1
Linear polarisiertes Licht durch Streuung
Fällt natürliches Licht auf eine Wanne mit trübem Wasser, dann wird an dessen suspendierten
Teilchen das Licht gestreut. Die Teilchen werden vom einfallenden Licht zu Schwingungen

angeregt, allerdings nur in der Ebene senkrecht zur Einfallsrichtung s . Betrachtet man das
Streulicht senkrecht zu dieser Richtung, dann beobachtet man nur noch linear polarisierte
Komponenten.

Das in Richtung s
abgestrahlte Licht
schwingt nur in der Ebene

s
Lichtquelle für
natürliches Licht
Die suspendierten Teilchen
werden zu Schwingungen in

der Ebene s angeregt
Abbildung 10 Schema zur Polarisation des von einer Suspension senkrecht zur

Einfallsrichtung s gestreuten Lichts. Die Pfeile zeigen die Schwingungsrichtung der
elektrischen Feldstärke. Aufgrund der Rayleigh Streuung ist das gestreute Licht bläulich, das
durchgehende gelblich gefärbt.
15
Für die Intensität des durchgehenden Strahls in Abhängigkeit vom Weg x im Medium gilt
das Rayleighsche Gesetz
I ( x )  I 0  e  h x
Die Schwächungskonstante h hängt aber von der Wellenlänge bzw. der Frequenz  der
Strahlung ab:
h ~ 4
Man erkennt, daß kurzwellige Strahlung stärker gestreut wird. Deshalb ist im durchgehenden
Strahl der Blau Anteil geschwächt und es dominiert die Komplementärfarbe Gelb. Man denke
z. B. an die Gelb bzw. Rotfärbung der Sonne, wenn ihr Licht morgens und abends unter
flachem Winkel ausgedehnte Luftschichten mit suspendierten Staubteilchen durchquert.
Dementsprechend ist das Streulicht komplementär dazu Blau bzw. Grün, was man von der
Färbung des Abendhimmels kennt
Versuch 6 Streuung an einer Suspension. In einer Wanne befindet sich mit Mastix getrübtes
Wasser. Mit einem Analysator erkennt man, daß das nach oben und das zur Seite gestreute
Licht linear polarisiert ist.
a) Wird die Suspension mit polarisiertem Licht beleuchtet, dann wird, je nach Stellung des
Polarisators, nur nach oben oder nach vorn abgestrahlt
b) Außerdem fällt auf, daß das gestreute Licht bläulich, das durchgehende Licht gelblich ist.
8.3.4.2
Polarisation durch Reflexion am Dielektrikum
Trifft ein Strahl von natürlichem Licht auf die Oberfläche einer Glasplatte, dann wird ein Teil
der Strahlung reflektiert, ein anderer dringt in das Medium ein. Die Strahlung wird im
Medium durch die Schwingung seiner Dipole fortgepflanzt. Steht die reflektierte Strahlung
senkrecht zu der ins Medium gebrochenen, dann sind beide Anteile senkrecht zueinander
linear polarisiert.
Einfallender
Strahl

s
B
Reflektierter
Strahl
B
90
°
Ins Medium
gebrochener
Strahl

Abbildung 11 Lineare Polarisation des reflektierten Strahls bei Reflexion unter dem Brewster
Winkel  B
16
Steht der reflektierte Strahl senkrecht zu dem im Medium fortlaufenden, dann gilt das
Brewstersche Gesetz:
n  tan  B
 B    90  180
Brewstersches Gesetz
Winkelsumme
  90   B
n
sin  B
sin  B
sin  B


sin 
sin( 90   B ) cos  B
Definition des Brechungsindex
Für Glas mit dem Brechungsindex n=1,5 beträgt der Brewster Winkel 56,3°. Durch Messung
des Brewster Winkels kann der Brechungsindex bestimmt werden.
Versuch 7 Der Brewster Winkel wird mit Hilfe von zwei Spiegeln nachgewiesen. Der
reflektierte Strahl verschwindet ganz, weil schon die einfallende Strahlung polarisiert ist. In
der Figur oben entspricht das einem einfallenden Strahl mit nur einer Komponente, die in der
Reflektionsebene liegt.
8.3.4.3
Linear polarisiertes Licht durch Doppelbrechung
Manche Kristalle, z. B. der Kalkspat, CaCO3, sind optisch anisotrop. In ihnen ist die
Lichtgeschwindigkeit richtungsabhängig. Insbesonders gibt es in ihnen Richtungen, in denen
sich unterschiedlich polarisierte Strahlung unterschiedlich schnell fortpflanzt.
Abbildung 12 Schema eines Kalkspatkristalls mit rhomboedrischer Form. Die optische Achse
steht senkrecht, sie ist die Achse mit 3-zähliger Symmetrie. Von den drei senkrecht dazu
stehenden 2-zähligen Achsen ist eine als waagrechte Linie eingezeichnet.
Die Achse mit höchster Symmetrie nennt man die optische Achse. Strahlt Licht in dieser
Richtung ein, dann ist die Lichtgeschwindigkeit für alle Polarisationsrichtungen konstant co .
Strahlt man aber senkrecht zu dieser Achse ein, dann gibt es zwei Polarisationsrichtungen, für
die unterschiedliche Lichtgeschwindigkeiten gelte: Licht mit dem elektrischen Feldvektor
senkrecht zur Achse läuft mit. Man nennt Strahlung dieser Art „ordentliches Licht“. Strahlung
mit dem elektrischen Feldvektor in Achsenrichtung heißt „außerordentliches Licht“, seine
17
Ausbreitungsgeschwindigkeit ist c ao . Im Kalkspat gilt cao  1,116  co , man nennt Kristalle
mit einer bevorzugten Richtung und cao  c0 „einachsig negativ“.
Optische
Achse

Vektoren E
des
elektrischen
Feldes

Wellenvektor k
Orte der Wellenfronten

für E senkrecht und
parallel zur opt. Achse
Abbildung 13 „Indikatrix“ zu einem optisch anisotropen, einachsig positiven Kristall
co  c a 0 . Die bunten Pfeile zeigen die Richtungen der Polarisation des elektrischen Feldes.
Sie stehen immer senkrecht zum Wellenvektor. Das orange Rotationsellipsoid zeigt den Ort
der Wellenfronten mit Polarisation parallel zur optischen Achse, die der außerordentlichen
Strahlen, die in alle Richtungen gleichzeitig von der Mitte ausgehen. Zum Vergleich ist grün
die Ausbreitungskugel für das Licht der ordentlichen Strahlen eingezeichnet. Nähert sich die
Ausbreitungsrichtung der optischen Achse, dann werden die Unterschiede kleiner. Im
Schnittpunkt mit der optischen Achse sind beide Ausbreitungsgeschwindigkeiten gleich, wie es
die Symmetrie erfordert.
Strahlt man mit natürlichem Licht senkrecht auf eine schräg zur optischen Achse stehende
Fläche eines Kalkspatkristalls, dann werden der ordentliche und außerordentliche Strahl
aufgespalten: Der ordentliche Strahl läuft ungebrochen durch den Kristall, der
außerordentliche Strahl wird- trotz senkrechtem Einfall- abgelenkt. Man bezeichnet diesen
Effekt als „Doppelbrechung“. Im Nicolschen Prisma wird einer der beiden Strahlen durch
Totalreflektion ausgeblendet, es wird nur der polarisierte, ordentliche Strahl durchgelassen.
Die Anisotropie ist die Voraussetzung für die Doppelbrechung. Deshalb beobachtet man in
mechanisch gespannten Material, auch in z. B. Glas oder Plastikfolien,
„Spannungsdoppelbrechung“.
18
Außerordentlicher
Strahl
Unpolarisier
tes Licht
senkrecht
zur
Oberfläche
Ordentlicher
Strahl
Abbildung 14 Doppelbrechung: Licht fällt senkrecht auf eine Fläche eines optisch
einachsigen Kristalls. Wenn die Fläche nicht senkrecht zur Hauptachse steht wird das Licht
in zwei Strahlen unterschiedlicher Polarisation und Ausbreitungsgeschwindigkeit aufgeteilt.
Wenn die Hauptachse nicht parallel zur Fläche liegt ( in der Zeichnung sei sie gegenüber der
Hauptachse geneigt), dann treten beide Strahlen an unterschiedlichen Stellen des Kristalls
aus. Diese Erscheinung nennt man Doppelbrechung.
Abbildung 15 Qualitative Konstruktion nach dem Huygens-Fresnelschen Prinzip zur
Veranschaulichung der beiden Wellenfelder mit unterschiedlicher
Ausbreitungsgeschwindigkeit. Die Ausbreitungsrichtungen werden gleich, wenn die
Oberfläche parallel zur optischen Achse liegt.
19
Manche doppelbrechenden Kristalle absorbieren das ordentliche und außerordentliche Licht
unterschiedlich stark: Man nennt diesen Effekt Dichroismus. Polarisationsfolien enthalten
anisotrope Einlagerungen dichroitischen Materials.
Versuch 8 a) Doppelbrechung am Kalkspat. b) Am Turmalin wird der Dichroismus gezeigt:
Das grüne durchfallende Licht ist polarisiert.
Versuch 9 Spannungsdoppelbrechung wird am verspannten Glas gezeigt.
8.3.4.4
Zirkular polarisiertes Licht und „  / 4 Plättchen“
Überlagert man zwei linear polarisierte Strahlen mit gleicher Ausbreitungsrichtung und
gleicher Frequenz aber zueinander senkrechten Feldvektoren, so erhält man eine zirkular
polarisierte Welle, wenn die beiden Wellenzüge  / 2 zueinander phasenverschoben sind, die
Komponenten der Amplitude verhalten sich also wie sin t und cost . Der Feldvektor läuft
dann auf einer Schraubenlinie um die Ausbreitungsrichtung.
Dipole, senkrecht
zueinander

B

s

B
Abbildung 16 Schema der um  / 2 gegeneinander phasenverschobenen Teilwellen, deren
Summe zirkular polarisiertes Licht ergibt
Eine Phasendifferenz stellt sich zwischen dem ordentlichen und unordentlichen Strahl beim
Durchtritt durch ein doppelbrechendes Medium ein, weil wegen der unterschiedlichen
Ausbreitungsgeschwindigkeit die eine Welle hinter der anderen herhinkt. Durch geeignete
Dicke eines Plättchens kann man gerade die Phasendifferenz  / 2 einstellen. Damit kann man
aus natürlichem Licht zirkular polarisiertes Licht erzeugen. Die Phasendifferenz entspricht
 / 4 , man nennt diese Plättchen deshalb „  / 4 Plättchen“.
Versuch 10 In einem Strahlengang mit Polarisator, „  / 4 Plättchen“ , Analysator und
Blaufilter (weil das „  / 4 Plättchen“ für Blau gilt) zeigt sich die zirkulare Polarisation
dadurch, daß der Analysator in allen Stellungen durchlässig ist.
20
8.3.4.5
Optische Aktivität
Moleküle, die sich durch einen Drehsinn auszeichnen, werden als links- oder rechts-„händig“,
oder, zusammenfassend, als „chiral“ (griechisch für händig) bezeichnet. Durchläuft
monochromatisches, linear polarisiertes Licht ein Medium mit chiralen Molekülen, dann ist
das Licht nach Durchtritt zwar linear polarisiert, aber mit gedrehter Polarisationsebene. Stoffe
mit dieser Eigenschaft, z.B. eine Rohrzuckerlösung, nennt man optisch aktiv.
Formal kann man sich die lineare Polarisation als Summe zweier gegenläufiger zirkular
polarisierter Wellen vorstellen. Wird eine davon im Medium gebremst, dann ist sie beim
Verlassen des Mediums in der Phase gegenüber der anderen versetzt. Addiert ergibt sich
wieder eine linear polarisierte Welle, aber mit gedrehter Polarisationsebene. Diese Erklärung
ist analog zu der des „  / 4 Plättchens“, nur sind die Komponenten jetzt zirkular polarisiert.
Die physikalische Erklärung wird mit einem Versuch deutlich, indem ca. 5 mm große linksund rechtsdrehende Spiralen aus Metall die Polarisationsebene von cm-Wellen drehen. Im
Feld einer Welle wirkt jede Spirale als Empfangs- und Sendeantenne. Die Abbildung unten
zeigt eine Spirale, die senkrecht zur Ausbreitungsrichtung der Welle liegt. Betrachtet man die

in ihr durch die Änderung der magnetische Feldstärke dB dt induzierten elektrischen Felder
und Ströme, dann addiert sich zum magnetischen Feldvektor ein zur ursprünglichen

Polarisationsebene senkrecht stehender magnetischer Anteil B  . Die Wellenlänge ist größer
als die Spirale, deshalb sind die Drehungen des Feldvektors auf beiden Seiten in Richtung und

Betrag unterschiedlich und heben sich nicht auf. Bei linksdrehender Spirale zeigt B  das
entgegengesetzte Vorzeichen, die Polarisationsebene dreht entsprechend in die andere
Richtung. Die auslaufende elektrische Feldstärke dreht um den gleichen Betrag in gleicher
Richtung. Auf analoge Weise drehen die Moleküle optisch aktiver Medien als mikroskopische
Sender und Antennen die Polarisationsebene des Lichtes.
Grundlage für die Konstruktion sind die Beziehungen zwischen Strom und elektrischen und
magnetischen Feldern gemäß den Maxwellschen Gleichungen (vgl. Abschnitt 6.6):

E
Faradaysches Induktionsgesetz:
„Ein sich zeitlich änderndes magnetisches
Feld erzeugt ein quellenfreies elektrisches
Feld“

B

B

E
Ampèresches Durchflutungsgesetz:
„Ströme oder ein sich zeitlich ändernder
elektrischer Fluß erzeugen ein magnetisches
Feld“
I
Tabelle 9 Das Induktions- und das Durchflutungsgesetz
21

dB
dt

E

k
Abbildung 17 Von links komme eine Welle, der Vektor der magnetischen Feldstärke liege in
der blauen Ebene. Die von links nach rechts abnehmende Farbstärke erinnere an die
abnehmende magnetische Feldstärke, weil die Wellenlänge größer als der Durchmesser der

Spirale ist. Die veränderliche Feldstärke dB dt in der Achse der Spirale induziert die

Feldstärke E .
I
B

B

B

Abbildung 18: Die Feldstärke E führt im Leiter zu einem Strom mit einer Komponente in
Richtung der Achse (dunkelblauer Pfeil). Zu diesem Strom gehört ein Magnetfeld (hellblauer

Kreisbogen) um den als Rohr abstrahierten Leiter. Durch den Beitrag B  dieses
Magnetfeldes wird die Polarisationsrichtung der auslaufenden Welle B gegenüber der

einlaufenden B um den rosa eingezeichneten Winkel  gedreht. Orange: elektrische,
hellblau: magnetische Feldstärke, dunkelblau: Strom.
Versuch 11 Die Polarisationsebene von Radarwellen wird durch Schrauben-förmige
Drahtstücke gedreht. Es wird zunächst die Polarisation durch Drehen des Empfängers
gezeigt. a) Rechtsschraube eingesetzt: Die Polarisationsebene dreht entsprechend b)
Linksschrauben eingesetzt: Die Polarisationsebene dreht in Gegenrichtung.
22